Утверждаю

Зам. директора по УПР

________ Мельник Л.В.

«___» _________ 2012 г.

Перечень вопросов для подготовки к экзамену

Дисциплина: Математика (I семестр)

Специальность: 2-40 01 01 Программное обеспечение информационных технологий

Специализация: 2-40 01 01 35 Программное обеспечение обработки экономической и деловой информации

Квалификация: Техник-программист

Преподаватель: Полейчук Э.А.

Рассмотрен на заседании цикловой комиссии

Протокол № ___ от ______________

Председатель цикловой комиссии Овчинникова Л.И.

Теоретические вопросы

1. Дайте определения основных понятий теории множеств, операций над множествами.

В основе теории множеств лежат первичные понятия: множество и отношение быть элементом множества (обозначается как   — «x есть элемент множества A», «x принадлежит множеству A»). Среди производных понятий наиболее важны следующие:

• пустое множество, обычно обозначается символом  ;

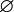• подмножество и надмножество;

• семейство множеств;

• пространство (Универсум);

• конституента.

Над множествами определены следующие операции:

• объединение (или сумма) (обозначается как  );

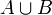• разность (обозначается как 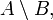  реже  );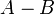

• дополнение (обозначается как 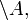  или  );

• пересечение (или произведение) (обозначается как  );

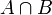• симметрическая разность (обозначается как 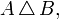  реже  ).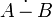

Для множеств определены следующие бинарные отношения:

• отношение равенства (обозначается как  );

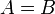• отношение включения (обозначается как  ).

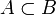2. Дайте определения высказывания, простого и составного высказывания, логических операций. Приведите примеры высказываний. Дайте определения логических операций с помощью таблиц истинности.

Высказывание — термин математической логики, обозначающий формализованную структурированную запись мысли с помощью буквенных символов и логических связок, рассматриваемую с точки зрения истинностных значений. Это утверждение, для которого оценивается логическое значение: ложь или истина^[1]. Логическое высказывание принято обозначать заглавными латинскими буквами. Является основным объектом логики высказываний.

Логические высказывания принято подразделять на два вида: элементарные логические высказывания и составные логические высказывания.

Составное логическое высказывание — это высказывание, образованное из других высказываний с помощью логических связок.

Логическая связка — это любая логическая операция над высказыванием. Например, употребляемые в обычной речи слова и словосочетания «не», «и», «или», «если… , то», «тогда и только тогда» являются логическими связками.

Элементарные логические высказывания — это высказывания не относящиеся к составным.

Примеры: «Петров — врач», «Петров — шахматист» — элементарные логические высказывания. «Петров — врач и шахматист» — составное логическое высказывание, состоящие из двух элементарных высказываний, связанных между собой при помощи связки «и».

Основные операции над логическими высказываниями

Отрицание логического высказывания — логическое высказывание, принимающее значение «истинно», если исходное высказывание ложно, и наоборот.

Конъюнкция двух логических высказываний — логическое высказывание, истинное только тогда, когда они одновременно истинны.

Дизъюнкция двух логических высказываний — логическое высказывание, истинное только тогда, когда хотя бы одно из них истинно.

Импликация двух логических высказываний A и B — логическое высказывание, ложное только тогда, когда B ложно, а A истинно.

Равносильность (эквивалентность) двух логических высказываний — логическое высказывание, истинное только тогда, когда они одновременно истинны или ложны.

Кванторное логическое высказывание с квантором всеобщности ( ) — логическое высказывание, истинное только тогда, когда для каждого объекта x из заданной совокупности высказывание A(x) истинно.

Кванторное логическое высказывание с квантором существования ( ) — логическое высказывание, истинное только тогда, когда в заданной совокупности существует объект x, такой, что высказывание A(x) истинно.