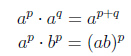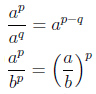Решение однородных тригонометрических уравнений
В
этой статье мы рассмотрим способ
решения однородных
тригонометрических уравнений.
Однородные тригонометрические уравненияимеют ту же структуру, что и однородные уравнения любого другого вида. Напомню способ решения однородных уравнений второй степени:
Рассмотрим
однородные уравнения вида
Отличительные признаки однородных уравнений:
а) все одночлены имеют одинаковую степень,
б) свободный член равен нулю,
в) в уравнении присутствуют степени с двумя различными основаниями.
Однородные уравнения решаются по сходному алгоритму.
Чтобы
решить уравнение такого типа, разделим
обе части уравнения на 
(можно
разделить на 
или
на 
)
Внимание! При делении правой и левой части уравнения на выражение, содержащее неизвестное, можно потерять корни. Поэтому необходимо проверить, не являются ли корни того выражения, на которое мы делим обе части уравнения, корнями исходного уравнения.
Если является, то мы выписываем этот корень, чтобы потом про него не забыть, а затем делим на это выражение.
Вообще, первым делом, при решении любого уравнения, в правой части которого стоит ноль, нужно попытаться разложить левую часть уравнения на множители любым доступным способом. А затем каждый множитель приравнять к нулю. В этом случае мы точно не потеряем корни.
Итак, осторожно разделим левую часть уравнения на выражение почленно. Получим:
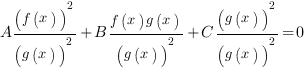
Сократим числитель и знаменатель второй и третьей дроби:
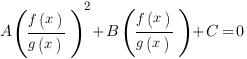
Введем замену:
,
Получим квадратное уравнение:
Решим
квадратное уравнение, найдем значения 
,
а затем вернемся к исходному
неизвестному.
При решении однородных тригонометрических уравнений, нужно помнить несколько важных вещей:
1. Свободный член можно преобразовать к квадрату синуса и косинуса с помощью основного тригонометрического тождества:
2. Синус и косинус двойного аргумента являются одночленами второй степени – синус двойного аргумента легко преобразовать к произведению синуса и косинуса, а косинус двойного аргумента – к квадрату синуса или косинуса:
Рассмотрим несколько примеров решения однородных тригонометрических уравнений.
1. Решим уравнение:
Это классический пример однородного тригонометрического уравнения первой степени: степень каждого одночлена равна единице, свободный член равен нулю.
Прежде
чем делить обе части уравнения
на 
, необходимо
проверить, что корни уравнения 
не
являются корнями исходного уравнения.
Проверяем: если
,
то 
,
следовательно их сумма не равна нулю.
Разделим обе части уравнения на .
Получим: 
,
где 
,
где
Ответ: , где
2. Решим уравнение:
Это пример однородного тригонометрического уравнения второй степени. Мы помним, что если мы можем разложить левую часть уравнения на множители, то желательно это сделать. В этом уравенении мы можем вынести за скобки . Сделаем это:
Приравняем каждый множитель к нулю:
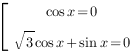
Решение
первого уравнения: 
,
где
Второе уравнение – однородное тригонометрическое уравнение первой степени. Чтобы его решить, разделим обе части уравнения на . Получим:
,
где
Ответ: , где ,
, где
3. Решим уравнение:
Чтобы
это уравнение «стало» однородным,
преобразуем 
в
произведение, и представим число 3 в
виде суммы квадратов синуса и косинуса:
Перенесем все слагаемые влево, раскроем скобки и приведем подобные члены. Получим:
Разложим левую часть на множители и приравняем каждый множитель к нулю:
Отсюда:
,
где
,
,
где
Ответ: , где ,
, где
4. Решим уравнение:
Мы
видим, что можем вынести за скобки 
.
Сделаем это:
Приравняем каждый множитель к нулю:
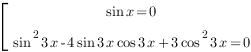
Решение первого уравнения:
,
где
Второе
уравнение совокупности представляет
собой классическое однородное уравнение
второй степени. Корни уравнения 
не
являются корнями исходного уравнения,
поэтому разделим обе части уравнения
на 
:
Отсюда:
Решение первого уравнения:
,
где
Решение второго уравнения:
,
где
Ответ: 
,
где
,
,
где
13
Понятие степени с натуральным показателем.
Степень
с натуральным показателем 
действительного
числа 
обозначается
как
и
определяется как результат умножения
числа
самого
на себя
раз.
В частных случаях, 
, 
, 
и
т.п.
Понятие степени с целым показателем.
Понятие
степени легко расширяется на случай
целого показателя. По определению,
если 
,
то 
, при
этом, значение 
не
определено.
Пусть
, 
,
тогда по определению
,
при этом, значение
не принадлежит множеству действительных чисел.
Понятие степени с рациональным показателем.
Для
определения степени с рациональным
показателем используют следующее
соотношение. Если 
и 
,
то
Свойства степени с рациональным показателем.
При умножении степеней с одинаковыми основаниями основание оставляют прежним, а показатели степеней складывают:
При делении степеней с одинаковыми основаниями основание оставляют прежним, а из показателя степени делимого вычитают показатель степени делителя:
При возведении степени в степень основание оставляют прежним, а показатели степеней перемножают:
Для
возведения в степень произведения нужно
возвести в степень с тем же показателем
каждый множитель, а полученные значения
перемножить. Если 
и 
,
то
При возведении
дроби в 
-ую
степень получится дробь, равная
отношению
-ой
степени числителя на
-ую
степень знаменателя. Если
и 
,
то
Обратим также внимание, что если и , то
Сравнение степеней с одинаковыми показателями
Пусть 
-
рациональное число и 
.
Тогда
при 
при 
Сравнение степеней с одинаковыми основаниями
Пусть
и 
-
рациональные числа и 
.
Тогда
при 
при 
Рассмотренные соотношение и их комбинации активно используются при осуществлении преобразований степенных выражений.
14
Степенью
называется выражение вида: 
,
где:
—
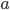основание
степени;
—
показатель
степени.
Степень с натуральным показателем {1, 2, 3,...}
Определем понятие степени, показатель которой — натуральное число (т.е. целое и положительное).
По определению:
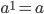.Возвести число в квадрат — значит умножить его само на себя:
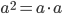
Возвести число в куб — значит умножить его само на себя три раза:
.
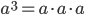Возвести
число в натуральную степень 
—
значит умножить число само на себя
раз:
Степень с целым показателем {0, ±1, ±2,...}
Если показателем степени является целое положительное число:
, n
> 0
Возведение в нулевую степень:
, a
≠ 0
Если показателем степени является целое отрицательное число:
, a
≠ 0
Прим:
выражение 
не
определено, в случае n
≤ 0.
Если n
> 0,
то 
Пример 1.
Степень с рациональным показателем
Если:
a > 0;
n — натуральное число;
m — целое число;
Тогда:
Пример 2.
Свойства степеней
Произведение степеней |
|
Деление степеней |
|
Возведение степени в степень |
|
Пример 3.
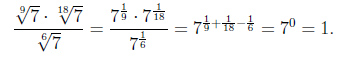
Корень
Арифметический квадратный корень
Уравнение 
имеет
два решения: x=2 и
x=-2. Это числа, квадрат которых равен 4.
Рассмотрим
уравнение 
.
Нарисуем график функции 
и
увидим, что и у этого уравнения два
решения, одно положительное, другое
отрицательное.
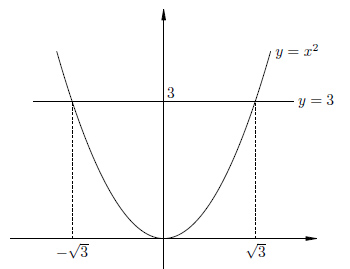
Но в данному случае решения не являются целыми числами. Более того, они не являются рациональными. Для того, чтобы записать эти иррациональные решения, мы вводим специальный символ квадратного корня.
Арифметический
квадратный корень 
—
это неотрицательное число, квадрат
которого равен
, a
≥ 0.
При a
< 0 —
выражение
не
определено, т.к. нет такого действительного
числа, квадрат которого равен отрицательному
числу
.
Корень из квадрата
Например, 
.
А решения уравнения
соответственно 
и 