
1 Градусная мера угла. Радианная мера угла. Перевод градусов в радианы и обратно.
Внимание! К этой теме имеются дополнительные материалы в Особом разделе 555. Для тех, кто сильно "не очень..." И для тех, кто "очень даже..." )
В предыдущем уроке мы освоили отсчёт углов на тригонометрическом круге. Узнали, как отсчитывать положительные и отрицательные углы. Осознали, как нарисовать угол больше 360 градусов. Пришла пора разобраться с измерением углов. Особенно с числом "Пи", которое так и норовит запутать нас в хитрых заданиях, да...
Стандартные задания по тригонометрии с числом "Пи" решаются неплохо. Зрительная память выручает. А вот любое отклонение от шаблона - валит наповал! Чтобы не свалиться - понимать надо. Что мы с успехом сейчас и сделаем. В смысле - всё поймём!
Итак, в чём считаются углы? В школьном курсе тригонометрии используются две меры: градусная мера угла и радианная мера угла. Разберём эти меры. Без этого в тригонометрии - никуда.
Градусная мера угла.
К градусам мы как-то привыкли. Геометрию худо-бедно проходили... Да и в жизни частенько встречаемся с фразой "повернул на 180 градусов", например. Градус, короче, штука простая...
Да? Ответьте мне тогда, что такое градус? Что, не получается с ходу? То-то...
Градусы придумали в Древнем Вавилоне. Давненько это было... Веков 40 назад... И придумали просто. Взяли и разбили окружность на 360 равных частей. 1 градус - это 1/360 часть окружности. И всё. Могли разбить на 100 частей. Или на 1000. Но разбили на 360. Кстати, почему именно на 360? Чем 360 лучше 100? 100, вроде, как-то ровнее... Попробуйте ответить на этот вопрос. Или слабо против Древнего Вавилона?
Где-то в то же время, в Древнем Египте мучились другим вопросом. Во сколько раз длина окружности больше длины её диаметра? И так измеряли, и этак... Всё получалось немного больше трёх. Но как-то лохмато получалось, неровно... Но они, египтяне не виноваты. После них ещё веков 35 мучились. Пока окончательно не доказали, что как бы мелко не нарезать окружность на равные кусочки, из таких кусочков составить ровно длину диаметра нельзя... В принципе нельзя. Ну, во сколько раз окружность больше диаметра установили, конечно. Примерно. В 3,1415926... раз.
Это и есть число "Пи". Вот уж лохматое, так лохматое. После запятой - бесконечное число цифр без всякого порядка... Такие числа называются иррациональными. Это, кстати, и означает, что из равных кусочков окружности диаметр ровно не сложить. Никогда.
Для практического применения принято запоминать всего две цифры после запятой. Запоминаем:
![]()
Раз уж мы поняли, что длина окружности больше диаметра в "Пи" раз, имеет смысл запомнить формулу длины окружности:
![]()
Где L - длина окружности, а d - её диаметр.
В геометрии пригодится.
Для общего образования добавлю, что число "Пи" сидит не только в геометрии... В самых различных разделах математики, а особенно в теории вероятности, это число возникает постоянно! Само по себе. Вне наших желаний. Вот так.
Но вернёмся к градусам. Вы сообразили, почему в Древнем Вавилоне круг разбили на 360 равных частей? А не на 100, к примеру? Нет? Ну ладно. Выскажу версию. У древних вавилонян не спросишь... Для строительства, или, скажем, астрономии, круг удобно делить на равные части. А теперь прикиньте, на какие числа делится нацело 100, и на какие - 360? И в каком варианте этих делителей нацело - больше? Людям такое деление очень удобно. Но...
Как выяснилось много позже Древнего Вавилона, не всем нравятся градусы. Высшей математике они не нравятся... Высшая математика - дама серьёзная, по законам природы устроена. И эта дама заявляет: "Вы сегодня на 360 частей круг разбили, завтра на 100 разобьёте, послезавтра на 245... И что мне делать? Нет уж..." Пришлось послушаться. Природу не обманешь...
Пришлось ввести меру угла, не зависящую от человеческих придумок. Знакомьтесь - радиан!
Радианная мера угла.
Что такое радиан? В основе определения радиана - всё равно окружность. Угол в 1 радиан, это угол, который вырезает из окружности дугу, длина которой (L) равна длине радиуса (R). Смотрим картинки.
Будем считать, что этот малюсенький угол имеет величину 1 градус:
Маленький такой угол, почти и нет его... Наводим курсор на картинку и видим примерно один радиан. L = R
Чувствуете разницу?
Один радиан много больше одного градуса. А во сколько раз?
Смотрим следующую картинку. На которой я нарисовал полукруг. Развёрнутый угол размером, естественно, в 180°.
А теперь я нарежу этот полукруг радианами! Наводим курсор на картинку и видим, что в 180° укладывается 3 с хвостиком радиана.
Кто угадает, чему равен этот хвостик!?
Да! Этот хвостик - 0,1415926.... Здравствуй, число "Пи", мы тебя ещё не забыли!
Действительно, в 180° градусах укладывается 3,1415926... радиан. Как вы сами понимаете, всё время писать 3,1415926... неудобно. Поэтому вместо этого бесконечного числа всегда пишут просто:
![]()
А вот в Интернете число
писать неудобно... Поэтому я в тексте пишу его по имени - "Пи". Не запутаетесь, поди?...
Вот теперь совершенно осмысленно можно записать приближённое равенство:
![]()
Или точное равенство:
![]()
Определим, сколько градусов в одном радиане. Как? Легко! Если в 3,14 радианах 180° градусов, то в 1 радиане в 3,14 раз меньше! То есть, мы делим первое уравнение (формула - это тоже уравнение!) на 3,14:

Это соотношение полезно запомнить В одном радиане примерно 60°. В тригонометрии очень часто приходится прикидывать, оценивать ситуацию. Вот тут это знание очень помогает.
Но главное умение этой темы - перевод градусов в радианы и обратно.
Если угол задан в радианах с числом "Пи", всё очень просто. Мы знаем, что "Пи" радиан = 180°. Вот и подставляем вместо "Пи" радиан - 180°. Получаем угол в градусах. Сокращаем, что сокращается, и ответ готов. Например, нам нужно выяснить, сколько градусов в угле "Пи"/2 радиан? Вот и пишем:

Или, более экзотическое выражение:

Легко, верно?
Обратный перевод чуть сложнее. Но не сильно. Если угол дан в градусах, мы должны сообразить, чему равен один градус в радианах, и умножить это число на количество градусов. Чему равен 1° в радианах?
Смотрим на формулу и соображаем, что если 180° = "Пи" радиан, то 1° в 180 раз меньше. Или, другими словами, делим уравнение (формула - это тоже уравнение!) на 180. Представлять "Пи" как 3,14 никакой нужды нет, его всё равно всегда буквой пишут. Получаем, что один градус равен:

Вот и всё. Умножаем число градусов на это значение и получаем угол в радианах. Например:

Или, аналогично:

Как видите, в неспешной беседе с лирическими отступлениями выяснилось, что радианы - это очень просто. Да и перевод без проблем... И "Пи" - вполне терпимая штука... Так откуда путаница!?
Вскрою тайну. Дело в том, что в тригонометрических функциях значок градусов - пишется. Всегда. Например, sin35°. Это синус 35 градусов. А значок радианов (рад) - не пишется! Он подразумевается. То ли лень математиков обуяла, то ли ещё что... Но решили не писать. Если внутри синуса - котангенса нет никаких значков, то угол - в радианах! Например, cos3 - это косинус трёх радианов.
Это и приводит к непоняткам... Человек видит "Пи" и считает, что это 180°. Всегда и везде. Это, кстати, срабатывает. До поры до времени, пока примеры - стандартные. Но "Пи" - это число! Число 3,14, а никакие не градусы! Это "Пи" радиан = 180°!
Ещё раз: "Пи" - это число! 3,14. Иррациональное, но число. Такое же, как 5 или 8. Можно, к примеру, сделать примерно "Пи" шагов. Три шага и ещё маленько. Или купить "Пи" килограммов конфет. Если продавец образованный попадётся...
"Пи" - это число! Что, достал я вас этой фразой? Вы уже всё давно поняли? Ну ладно. Проверим. Скажите-ка, какое число больше?

или

Или, что меньше?
cos4°
или
cos4 ?
Это из серии слегка нестандартных вопросов, которые могут и в ступор вогнать...
Если вы тоже в ступор впали, вспоминаем заклинание: "Пи" - это число! 3,14. В самом первом синусе четко указано, что угол - в градусах! Стало быть, заменять "Пи" на 180° - нельзя! "Пи" градусов - это примерно 3,14°. Следовательно, можно записать:

Во втором синусе обозначений никаких нет. Значит, там - радианы! Вот здесь замена "Пи" на 180° вполне прокатит. Переводим радианы в градусы, как написано выше, получаем:

Осталось сравнить эти два синуса. Что. забыли, как? С помощью тригонометрического круга, конечно! Рисуем круг, рисуем примерные углы в 60° и 1,05°. Смотрим, какие синусы у этих углов. Короче, всё, как в конце темы про тригонометрический круг расписано. На круге (даже самом кривом!) будет чётко видно, чтоsin60° существенно больше, чем sin1,05°.
Совершенно аналогично поступим и с косинусами. На круге нарисуем углы примерно 4 градуса и 4 радиана (не забыли, чему примерно равен 1 радиан?). Круг всё и скажет! Конечно, cos4 меньше cos4°.
Потренируемся в обращении с мерами угла.
Переведите эти углы из градусной меры в радианную:
360°; 30°; 90°; 270°; 45°; 0°; 180°; 60°
У вас должны получиться такие значения в радианах (в другом порядке!)
0 |
|
|
|
|
|
|
|
|
|
Я, между прочим, специально выделил ответы в две строчки. Ну-ка, сообразим, что за углы в первой строчке? Хоть в градусах, хоть в радианах?
Да! Это оси системы координат! Если смотреть по тригонометрическому кругу, то подвижная сторона угла при этих значениях точно попадает на оси. Эти значения нужно знать железно. И угол 0 градусов (0 радиан) я отметил не зря. А то некоторые этот угол никак на круге найти не могут... И, соответственно, в тригонометрических функциях нуля путаются... Другое дело, что положение подвижной стороны в нуле градусов совпадает с положением в 360°, так совпадения на круге - сплошь и рядом.
Во второй строчке - тоже углы специальные... Это 30°, 45° и 60°. И что в них такого специального? Особо - ничего. Единственное отличие этих углов от всех остальных - именно про эти углы вы должны знать всё. И где они располагаются, и какие у этих углов тригонометрические функции. Скажем, значение sin100° вы знать не обязаны. А sin45° - уж будьте любезны! Это обязательные знания, без которых в тригонометрии делать нечего... Но об этом подробнее - в следующем уроке.
А пока продолжим тренировку. Переведите эти углы из радианной меры в градусную:
|
|
|
|
|
|
|
|
|
У вас должны получиться такие результаты (в беспорядке):
210°; 150°; 135°; 120°; 330°; 315°; 300°; 240°; 225°.
Получилось? Тогда можно считать, что перевод градусов в радианы и обратно - уже не ваша проблема.) Но перевод углов - это первый шаг к постижению тригонометрии. Там же ещё с синусами-косинусами работать надо. Да и с тангенсами, котангенсами тоже...
Второй мощный шаг - это умение определять положение любого угла на тригонометрическом круге. И в градусах, и в радианах. Про это самое умение я буду вам во всей тригонометрии занудно намекать, да...) Если вы всё знаете (или думаете, что всё знаете) про тригонометрический круг, и отсчёт углов на тригонометрическом круге, можете провериться. Решите эти несложные задания:
1. В какую четверть попадают углы:
45°, 175°, 355°, 91°, 355° ?
Легко? Продолжаем:
2. В какую четверть попадают углы:
402°, 535°, 3000°, -45°, -325°, -3000°?
Тоже без проблем? Ну, смотрите...)
3. Сможете разместить по четвертям углы:

Смогли? Ну вы даёте..)
4. На какие оси попадёт уголок:
![]()
и уголок:

Тоже легко? Хм...)
5. В какую четверть попадают углы:

И это получилось!? Ну, тогда я прям не знаю...)
6. Определить, в какую четверть попадают углы:
1, 2, 3 и 20 радианов.
Ответ дам только на последний вопрос (он слегка хитрый) последнего задания. Угол в 20 радианов попадёт в первую четверть.
Остальные ответы не дам не из жадности.) Просто, если вы не решили чего-то, сомневаетесь в результате, или на задание №4 потратили больше 10 секунд, вы слабо ориентируетесь в круге. Это будет вашей проблемой во всей тригонометрии. Лучше от неё (проблемы, а не тригонометрии!)) избавиться сразу. Это можно сделать в теме: Практическая работа с тригонометрическим кругом в разделе 555.
Там рассказано, как просто и правильно решать такие задания. Ну и эти задания решены, разумеется. И четвёртое задание решено за 10 секунд. Да так решено, что любой сможет!
Если же вы абсолютно уверены в своих ответах и вас не интересуют простые и безотказные способы работы с радианами - можете не посещать 555. Не настаиваю.)
Хорошее понимание - достаточно веская причина, чтобы двигаться дальше!)
а) Область определения: D (cos x) = R .
б) Множество значений: E (cos x ) = [ – 1 , 1 ] . в) Четность, нечетность: функция четная.
г)
Периодичность:
функция периодическая с основным
периодом T = 2![]() .
.
д) Нули
функции:
cos x =
0 при x = ![]() +
n, n
+
n, n ![]() Z.
Z.
е) Промежутки знакопостоянства:
![]() ;
;
![]() .
.
. ж) Промежутки монотонности:
![]() ;
;
![]() .
.
з) Экстремумы:
![]() ;
; ![]() .
.
График функции y= cos x изображен на рисунке.
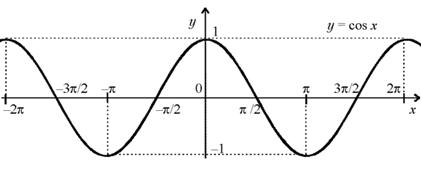
2
а) Область определения: D (sin x) = R .
б) Множество значений: E (sin x) = [ – 1 , 1 ] . в) Четность, нечетность: функция нечетная.
г) Периодичность: функция периодическая с основным периодом T = 2 .
д) Нули функции: sin x = 0 при x = n, n Z.
е) Промежутки знакопостоянства:
![]() ;
; ![]() .
.
ж) Промежутки
монотонности:
![]() ;
;
![]() .
.
з) Экстремумы:
![]() ;
; ![]() .
.
График функции y= sin x изображен на рисунке.
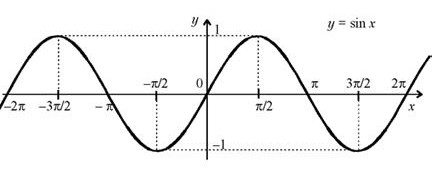
3
а) Область определения: D (tg x) = R \ { /2 + n( n Z ) }.
б) Множество значений: E (tg x ) = R . в) Четность, нечетность: функция нечетная.
г) Периодичность: функция периодическая с основным периодом T = .
д) Нули функции: tg x = 0 при x = n, n Z.
е) Промежутки знакопостоянства:
![]() ;
;
![]() .
.
ж) Промежутки монотонности: функция возрастает на каждом интервале, целиком принадлежащем ее области определения.
з) Экстремумы: нет.
График функции y = tg x изображен на рисунке.
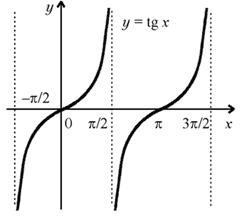
4
синус-это отношение противолежащего катета к гипотенузе косинус- это отношение прилежащего катета к гипотенузе тангенс-это отношение противолежащего катета к прилежащему катету котангенс-это отношение прилежащего катета к противолежащему катету
5
Обратные тригонометрические функции и их свойства. Арксинус, арккосинус, арктангенс, арккотангенс.
Функция ![]() :
:
 ;
; ;
; ;
;функция нечетная, то есть
 ;
; ;
; ;
; ;
; ;
; .
.
Функция ![]() :
:
;
 ;
;убывает на ;
функция ни четная, ни нечетная, то есть
 ;
; ;
; ;
; ;
; .
.
Функция ![]() :
:
 ;
;;
возрастает на промежутке
 ;
;функция нечетная, то есть
 ;
; ;
; ;
; ;
;график функции имеет 2 ассимптоты
 ;
;
Функция ![]() :
:
;
;
убывает на промежутке ;
функция ни четная, ни нечетная, то есть
 ;
; ;
; ;
;график функции имеет 2 ассимптоты
 .
.
7
териал из Википедии — свободной энциклопедии
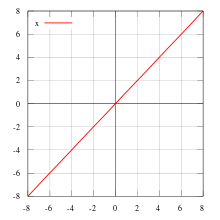
Нечётными и чётными называются функции, графики которых обладают симметрией относительно изменения знака аргумента. Это понятие важно во многих областях математического анализа, таких как теория степенных рядов и рядов Фурье. Такое название возникло как обобщение чётности степенных функций: функция f(x) = xn чётна тогда и только тогда, когда n чётно, и нечётна тогда и только тогда, когда n нечётно.
![]()
![]() —
пример
нечётной функции.
—
пример
нечётной функции.
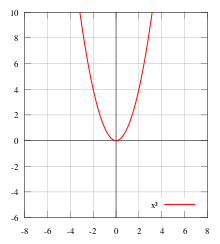
![]() —
пример
чётной функции.
—
пример
чётной функции.
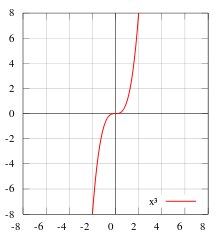
![]() нечётная
нечётная
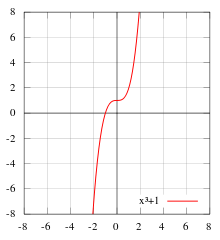
![]() ни
чётная, ни нечётная.
ни
чётная, ни нечётная.
Другие определения:
Нечётная функция — функция, меняющая знак при изменении знака независимого переменного (симметричная относительно центра координат).
Чётная функция — функция, не изменяющая своего значения при изменении знака независимого переменного (симметричная относительно оси ординат).
Индифферентная функция[источник не указан 257 дней] — функция, не обладающая симметрией. В эту категорию относят функции не подпадающие под предыдущие 2 категории.
Содержание [убрать]
|
[править]Определения
Определения
вводятся для любой симметричной
относительно нуля области определения ![]() ,
например, отрезка или интервала.
,
например, отрезка или интервала.
Функция
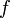 называется
чётной, если справедливо равенство
называется
чётной, если справедливо равенство
![]()
Функция
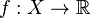 называется
нечётной, если справедливо равенство
называется
нечётной, если справедливо равенство
![]()
Если не выполняется ни одно из этих равенств, то функция называется индифферентной[источник не указан 257 дней]
(или функцией общего вида).
[править]Свойства
График нечётной функции симметричен относительно начала координат
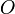 .
.График чётной функции симметричен относительно оси ординат
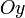 .
.Произвольная функция
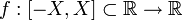 может
быть единственным образом представлена
в виде суммы нечётной и чётной функций:
может
быть единственным образом представлена
в виде суммы нечётной и чётной функций:
![]()
где
![]()
Функция
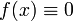 —
единственная функция, одновременно
являющаяся нечётной и чётной.
—
единственная функция, одновременно
являющаяся нечётной и чётной.Сумма, разность и вообще любая линейная комбинация чётных функций чётна, а нечётных — нечётна.
Функция, обратная чётной, чётна, а нечётной — нечётна.
Произведение двух функций одной чётности чётно.
Произведение двух функций разной чётности нечётно.
Композиция двух нечётных функций нечётна.
Композиция чётной функции с чётной/нечётной чётна.
Композиция любой функции с чётной чётна (но не наоборот!).
Производная чётной функции нечётна, а нечётной — чётна.
То же верно про производную третьего, пятого и вообще любого нечётного порядка.
Производная чётного порядка имеет ту же чётность, что и первоначальная функция.
[править]Примеры
[править]Нечётные функции
Нечётная степень
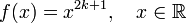 где
где 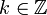 —
произвольное целое
число.
—
произвольное целое
число.Синус
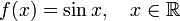 .
.Тангенс
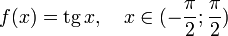 .
.
[править]Чётные функции
Чётная степень
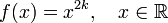 где
—
произвольное целое
число.
где
—
произвольное целое
число.Косинус
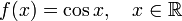 .
.Абсолютная величина (модуль)
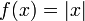 .
.
[править]Вариации и обобщения
8
Определение : Числовой функцией называется соответствие, которое каждому числу х из некоторого заданного множества сопоставляет единственное число y.
Обозначение:
y = f(x),
где x – независимая переменная (аргумент), y – зависимая переменная (функция). Множество значений x называется областью определения функции (обозначается D(f)). Множество значений y называется областью значений функции (обозначается E(f)). Графиком функции называется множество точек плоскости с координатами (x, f(x))

Способы задания функции.
аналитический способ (с помощью математической формулы);
табличный способ (с помощью таблицы);
описательный способ (с помощью словесного описания);
графический способ (с помощью графика).
Основные свойства функции.
1. Четность и нечетность
Функция называется четной, если – область определения функции симметрична относительно нуля – для любого х из области определения f(-x) = f(x)

График четной функции симметричен относительно оси 0y
Функция называется нечетной, если – область определения функции симметрична относительно нуля – для любого х из области определения f(-x) = –f(x)

График нечетной функции симметричен относительно начала координат.
2.Периодичность
Функция
f(x) называется периодической с периодом ![]() ,
если для любого х из области определения f(x)
= f(x+Т) = f(x-Т).
,
если для любого х из области определения f(x)
= f(x+Т) = f(x-Т).

График периодической функции состоит из неограниченно повторяющихся одинаковых фрагментов.
3. Монотонность (возрастание, убывание)
Функция f(x) возрастает на множестве Р , если для любых x1 и x2 из этого множества, таких, что x1 < x2 выполнено неравенство f(x1)< f(x2).

Функция f(x) убывает на множестве Р , если для любых x1 и x2 из этого множества, таких, что x1 < x2 выполнено неравенство f(x1) > f(x2).

4. Экстремумы
Точка
Хmax называется
точкой максимума функции f(x) , если для
всех х из некоторой окрестности Хmax ,
выполнено неравенство f(х)![]() f(Xmax).
f(Xmax).
Значение Ymax=f(Xmax) называется максимумом этой функции.

Хmax – точка максимума Уmax – максимум
Точка
Хmin называется
точкой минимума функции f(x) , если для
всех х из некоторой окрестности Хmin ,
выполнено неравенство f(х)![]() f(Xmin).
f(Xmin).
Значение Ymin=f(Xmin) называется минимумом этой функции.

Xmin – точка минимума Ymin – минимум
Xmin, Хmax – точки экстремума Ymin, Уmax – экстремумы.
5. Нули функции
Нулем функции y = f(x) называется такое значение аргумента х , при котором функция обращается в нуль: f(x) = 0.

Х1,Х2,Х3 – нули функции y = f(x).

Рекомендации к теме теория >>
Изучив эту тему, Вы должны уметь находить область определения различных функций, определять с помощью графиков промежутки монотонности функции, исследовать функции на четность и нечетность. Рассмотрим решение подобных задач на следующих примерах.
Примеры.
1. Найти область определения функции.
a) ![]()
Решение: область определения функции находится из условия

Ответ: ![]()
б) ![]()
Решение: область определения функции находится из условий
![]()
![]()
Ответ:![]()
2. Исследовать на четность и нечетность функцию:
a) ![]()
Решение:
1) |
|
![]() -
симметрична относительно нуля.
-
симметрична относительно нуля.
2) |
|
следовательно, функция f(x) – четная.
Ответ: четная.
в) ![]()
1) ![]()
D(f) = [-1; 1] – симметрична относительно нуля.
2) |
|
следовательно, функция не является ни четной, ни нечетной.
Ответ: ни четная, ни не четная.
9
Преобразования графиков функций — это линейные преобразования функции y = f(x) или её аргумента x к виду y = af(kx + b) + m, а также преобразование с использованием модуля.
Зная,
как строить графики функции y
= f(x), где y
= kx + b, y = ax2, y
= xn , y=xk, y
= sin x, y = cosx, y = tgx, y = ctgx, y=ax![]() y=logax ,
можно построить график
функции y = af(kx + b) + m.
y=logax ,
можно построить график
функции y = af(kx + b) + m.
Общий вид функции |
Преобразования |
y = f(x - b) |
Параллельный перенос графика вдоль оси абсцисс на | b | единиц
|
y = f(x + b) |
|
y = f(x) + m |
Параллельный перенос графика вдоль оси ординат на | m | единиц
|
|
Отражение графика |
y = f( - x) |
Симметричное отражение графика относительно оси ординат. |
y = - f(x) |
Симметричное отражение графика относительно оси абсцисс. |
|
Сжатие и растяжение графика |
y = f(kx) |
|
y = kf(x) |
|
|
Преобразования графика с модулем |
y = | f(x) | |
|
y = f( | x | ) |
|

10
Формулы приведения

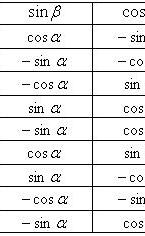
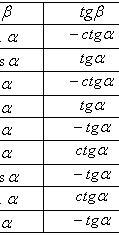
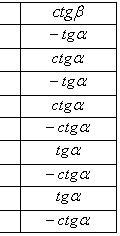
Основные тригонометрические тождества
![]()
![]()
![]()
![]()
Выражение тригонометрических функций через одну из них того же аргумента
(выбор
знака перед корнем зависит от того, в
какой четверти находится угол ![]() )
)
Через ![]() :
:
![]()
![]()
Через ![]() :
:
![]()
![]()
-1-2-3-4-5-6-
11
