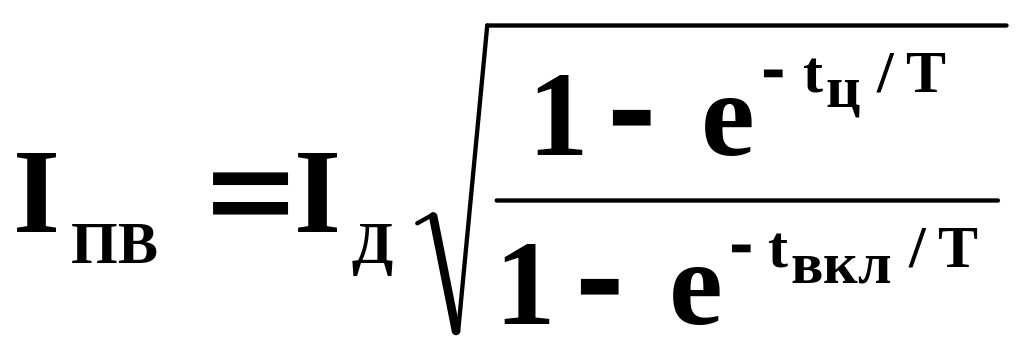- •Конспект лекций по курсу « пэму»
- •1.Общие вопросы проектирования электрических машин
- •1.1.Технико – экономические показатели эм
- •1.1.1.Экономические критерии оценки спроектированных изделий
- •1.1.2.Конструктивные формы исполнения электрических машин
- •1.1.3.Материалы, применяемые в электромашиностроении
- •Магнитные материалы
- •Проводниковые материалы
- •Изоляционные материалы
- •1.2.Главные размеры и электромагнитные нагрузки
- •1.2.1.Соотношения в геометрически подобных машинах (законы подобия)
- •Зависимость мощности гпм от линейных размеров
- •Изменение условий охлаждения с ростом мощности гпм
- •1.3.Расчет магнитных цепей электрических машин
- •1.3.1.Расчет мдс воздушного зазора
- •1.3.2.Расчет мдс зубцовой зоны
- •1.4.Потери мощности в электрических машинах
- •1.5.Расчет параметров обмоток
- •2.Тепловые и вентиляционные расчеты электрических машин
- •2.1.Режимы работы электрических машин
- •2.2.Виды, способы и системы охлаждения электрических машин
- •2.3.Оценка систем охлаждения
- •2.3.1.Коэффициенты, характеризующие тепловую нагрузку машины
- •2.3.2.Коэффициенты, характеризующие эффективностьспособов охлаждения
- •2.3.3. Коэффициенты, характеризующие разработанную систему охлаждения
- •2.3.4.Коэффициенты, характеризующие экономичность охлаждения
- •2.4.Характеристика вентиляционной сети
- •2.5.Вентиляторы электрических машин
- •2.6.Виды теплообмена в электрических машинах
- •2.7.Нагрев однородного тела
- •2.8.Теплопередача в телах простейшей конфигурации
- •2.8.1.Плоская стенка без внутренних потерь
- •2.8.2.Полый цилиндр
- •2.8.3.Теплопередача вдоль стержня
- •2.8.4.Плоская стенка с внутренними потерями
- •2.9.Нагрев и охлаждение однородного проводника
- •2.9.1.Нагрев однородного проводника в режиме s1.
- •2.9.2.Нагрев проводника в кратковременном режиме
- •2.9.3.Нагрев проводника в повторно - кратковременном режиме
- •2.9.4.Нагрев неоднородного проводника
- •2.10.Нагрев цилиндрических катушек
- •2.11.Нагрев проводника в режиме короткого замыкания
- •2.12.Современные методы тепловых расчетов электрических машин
- •2.12.1.Метод температурных полей
- •2.12.2.Метод тепловых параметров
- •2.12.3.Метод эквивалентных тепловых схем (этс)
- •3.Проектирование ад
- •3.1.Структура серии
- •3.2.Главные размеры и электромагнитные нагрузки ад
- •3.3.Обмотки статоров асинхронных двигателей
- •3.4.Выбор числа пазов статора и ротора
- •3.5.Высшие гармоники магнитного поля в воздушном зазоре
- •3.6.Пазы статора
- •3.6.1.Пазовые клинья
- •3.7.Источники шума и вибраций асинхронных двигателей
- •3.8.Выбор формы пазов ротора
- •3.9.Расчет размеров стержней ротора
- •3.10.Выбор воздушного зазора ад
- •3.11.Расчет магнитной цепи ад
- •3.12.Особенности взрывозащищенных ад
- •3.13.Расчет рабочих характеристик ад
- •3.14.Расчет пусковых характеристик ад
- •3.15.Расчет пуска асинхронных двигателей
- •4.Проектирование машин постоянного тока
- •4.1.Главные размеры и электромагнитные нагрузки мпт
- •4.2.Выбор главных размеров
- •4.3.Учет требований надежности при проектировании машин постоянного тока
- •4.4.Необходимость применения компенсационной обмотки
- •4.5.Выбор числа пар полюсов машин постоянного тока
- •4.6.Расчет обмотки якоря
- •4.6.1.Условия симметрии обмоток
- •4.6.2.Простая волновая обмотка
- •4.6.3.Сложная волновая обмотка
- •4.6.4.Простая петлевая обмотка
- •4.6.5.Сложная петлевая обмотка
- •4.6.6.Комбинированная обмотка
- •4.7.Выбор типа обмотки якоря
- •4.8.Выбор размеров проводников и пазов
- •4.9.Расчет магнитных цепей мпт
- •4.9.1.Выбор воздушного зазора
- •4.9.2.Размеры сердечника главного полюса
- •4.9.3.Размеры станины
- •4.10.Определение размеров и числа щеток и размеров коллектора
- •4.11.Коммутация мпт
- •4.11.1.Эдс, наводимые в коммутируемой секции.
- •4.12.Расчет обмоток добавочных полюсов и компенсационной.
- •4.13.Расчет мдс обмотки возбуждения
- •5.Проектирование синхронных машин
- •5.1.Основные конструктивные формы исполнения см
- •5.1.1.Особенности выбора главных размеров см различных типов
- •5.2.Обмотки статоров см
- •5.3.Выбор величины воздушного зазора см
- •5.4.Успокоительная (пусковая) обмотка
- •5.5.Расчет мдс реакции якоря
- •6.Общие вопросы проектирования трансформаторов
- •6.1.Краткая характеристика систем охлаждения трансформаторов
- •6.2.Выбор конструкции и расчет обмоток трансформаторов
- •6.2.1.Цилиндрические обмотки из прямоугольного провода
- •6.2.2.Многослойные цилиндрические обмотки из круглого провода
- •6.2.3.Винтовые обмотки
- •6.2.4.Катушечные обмотки
- •6.3.Расчет магнитной системы трансформатора
- •6.4.Расчет параметров короткого замыкания трансформаторов
- •Методические указания
- •7.Исходные данные для выполнения курсового проекта
- •8.Выбор главных размеров
- •9.Расчет данных обмотки статора
- •10.Расчет размеров зубцовой зоны статора
- •11.Расчет ротора
- •12.Расчет намагничивающего тока
- •13.Параметры рабочего режима
- •14.Расчет рабочих характеристик
- •15.Расчет пусковых характеристик
- •16.Тепловой и вентиляционный расчеты
- •17.Содержание расчетно – пояснительной записки и графической части проекта
2.8.4.Плоская стенка с внутренними потерями
Предположим, что стенка имеет
размер
![]() в направлении оси
,
а размеры стенки в направлении осей
и
значительно больше
.
В связи с этим полагаем, что:
в направлении оси
,
а размеры стенки в направлении осей
и
значительно больше
.
В связи с этим полагаем, что:
;
Рассматриваем установившийся
нагрев и считаем, что удельная
теплопроводность не зависит от
температуры. Предполагаем, что по всему
объему стенки равномерно распределены
потери объемной плотностью
![]() .
Принимаем также, что температура
окружающей среды и условия теплоотдачи
по обе стороны стенки одинаковы. При
этих допущениях дифференциальное
уравнение нагрева имеет вид:
.
Принимаем также, что температура
окружающей среды и условия теплоотдачи
по обе стороны стенки одинаковы. При
этих допущениях дифференциальное
уравнение нагрева имеет вид:
![]()
В общем виде решение уравнения
![]()
Граничное условие задаем в виде:
При
![]()
![]()
Получаем выражение для
константы
![]() :
:
![]()
Тогда окончательное распределение температуры имеет вид:
![]()
Если задать в качестве граничных условий температуру окружающей среды и коэффициент теплоотдачи с поверхности, получим следующее распределение температуры:
![]()
2.9.Нагрев и охлаждение однородного проводника
Однородным будем считать проводник, у которого по всей длине остаются неизменными поперечное сечение, периметр, условия теплоотдачи с поверхности и физические свойства.
2.9.1.Нагрев однородного проводника в режиме s1.
Количество тепла, выделяющееся
в единице длины проводника при протекании
по нему тока
![]() за время
:
за время
:
![]()
где - удельное сопротивление материала проводника, приведенное к температуре :
![]()
![]() - удельное сопротивление
материала проводника при температуре
окружающей среды;
- удельное сопротивление
материала проводника при температуре
окружающей среды;
![]() - температурный коэффициент сопротивления;
- температурный коэффициент сопротивления;
![]() - превышение температуры
проводника;
- коэффициент вытеснения тока;
- превышение температуры
проводника;
- коэффициент вытеснения тока;
![]() - сечение проводника.
- сечение проводника.
Количество тепла, затрачиваемое на нагрев проводника:
![]()
где
![]() - плотность материала проводника.
- плотность материала проводника.
Количество тепла, отдаваемое с поверхности проводника в окружающую среду:
![]()
В общем виде уравнение теплового баланса имеет вид:
![]()
Решение уравнения получаем в таком виде:
где - установившееся превышение температуры:
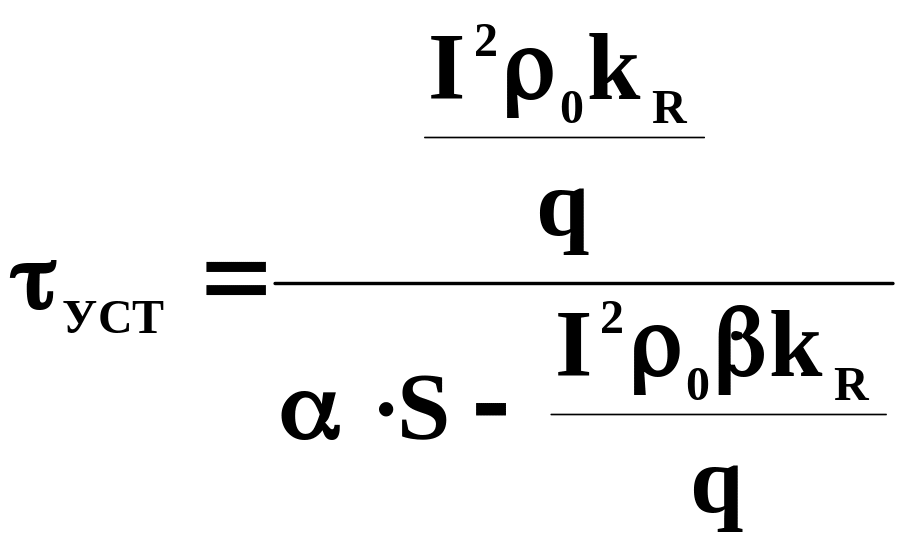
- постоянная времени нагрева:

Дифференциальное уравнение
остывания можно получить из дифференциального
уравнения нагрева, если принять
![]() .
.
Во многих случаях целесообразно
для упрощения расчетов принять
![]() ,
т. е. не учитывать зависимость удельного
сопротивления от температуры. При этом
установившееся превышение температуры
равно:
,
т. е. не учитывать зависимость удельного
сопротивления от температуры. При этом
установившееся превышение температуры
равно:
![]()
2.9.2.Нагрев проводника в кратковременном режиме
Задача расчета – подобрать
такой ток кратковременного режима
![]() ,
при котором за время
,
при котором за время
![]() проводник нагреется до такой же
температуры, как и при протекании в
продолжительном режиме тока
проводник нагреется до такой же
температуры, как и при протекании в
продолжительном режиме тока
![]() .
Установившееся превышение температуры
в продолжительном режиме при условии
:
.
Установившееся превышение температуры
в продолжительном режиме при условии
:
![]()
Превышение температуры по окончании времени кратковременного режима:
![]()
Приравнивая полученные превышения температур, получим соотношение между токами кратковременного и продолжительного режима:
![]()
2.9.3.Нагрев проводника в повторно - кратковременном режиме
Задача расчета – подобрать
такой ток повторно - кратковременного
режима
![]() ,
при котором за время
,
при котором за время
![]() проводник нагреется до такой же
температуры, как и при протекании в
продолжительном режиме тока
.
Установившееся превышение температуры
в продолжительном режиме при условии
:
проводник нагреется до такой же
температуры, как и при протекании в
продолжительном режиме тока
.
Установившееся превышение температуры
в продолжительном режиме при условии
:
Максимальное превышение температуры в квазиустановившемся режиме нагрева:
![]()
где
![]() - установившееся превышение температуры
в продолжительном режиме при протекании
тока
;
- установившееся превышение температуры
в продолжительном режиме при протекании
тока
;
![]() и
и
![]() - время включения и время цикла
соответственно.
- время включения и время цикла
соответственно.
Приравнивая полученные превышения температур, получим соотношение между токами повторно - кратковременного и продолжительного режима: