1.1 Схема шифрования с открытым ключом

Пусть К – пространство ключей, а e и d – ключи шифрования и расшифрования соответственно. E_e – функция шифрования для произвольного ключа e , такая что: E_e(m) = c.

Здесь , где C – пространство шифротекстов, а , где M – пространство сообщений.

D_d – функция расшифрования, с помощью которой можно найти исходное сообщение m, зная шифротекст c: D_d(c) = m.

{E_e: } – набор шифрования, а {D_d: } – соответствующий набор для расшифрования. Каждая пара (E,D) имеет свойство: зная E_e, невозможно решить уравнение E_e(m) = c, то есть для данного произвольного шифротекста , невозможно найти сообщение . Это значит, что по данному e невозможно определить соответствующий ключ расшифрования d. E_e является односторонней функцией, а d – лазейкой.

На рисунке 1 показана схема передачи информации лицом А лицу В. Они могут быть как физическими лицами, так и организациями и так далее. Но для более лёгкого восприятия принято участников передачи отождествлять с людьми, чаще всего именуемыми Алиса и Боб. Участника, который стремится перехватить и расшифровать сообщения Алисы и Боба, чаще всего называют Евой.

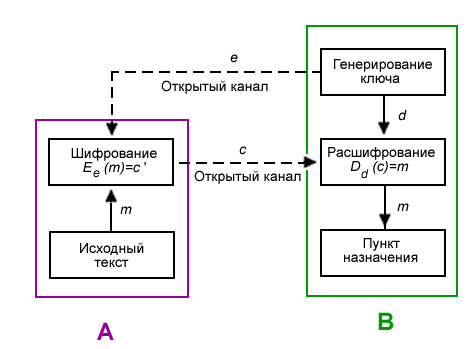
Рис. 1. Схема шифрования с открытым ключом

1. Боб выбирает пару (e, d) и шлёт ключ шифрования e (открытый ключ) Алисе по открытому каналу, а ключ расшифрования d (закрытый ключ) защищён и секретен (он не должен передаваться по открытому каналу).

2. Чтобы послать сообщение m Бобу, Алиса применяет функцию шифрования, определённую открытым ключом e: E_e(m) = c, c – полученный шифротекст.

3. Боб расшифровывает шифротекст c, применяя обратное преобразование D_d, однозначно определённое значением d.

2 Алгоритм rsa

Опубликованная в ноябре 1976 года статья Уитфилда Диффи и Мартина Хеллмана «Новые направления в криптографии» (англ. New Directions in Cryptography) перевернула представление о криптографических системах, заложив основы криптографии с открытым ключом. Разработанный впоследствии алгоритм Диффи – Хеллмана позволял двум сторонам получить общий секретный ключ, используя незащищенный канал связи. Однако этот алгоритм не решал проблему аутентификации. Без дополнительных средств пользователи не могли быть уверены, с кем именно они сгенерировали общий секретный ключ.

Изучив эту статью, трое учёных Рональд Ривест, Ади Шамир и Леонард Адлеман из Массачусетского технологического института (MIT) приступили к поискам математической функции, которая бы позволяла реализовать сформулированную Уитфилдом Диффи и Мартином Хеллманом модель криптографической системы с открытым ключом. После работы над более чем 40 возможными вариантами, им удалось найти алгоритм, основанный на различии в том, насколько легко находить большие простые числа и насколько сложно раскладывать на множители произведение двух больших простых чисел, получивший впоследствии название RSA. Система была названа по первым буквам фамилий её создателей.

Алгоритм RSA основывается на использовании односторонних функций шифрования которые обладают свойством:

• Если x известно, то f(x) вычислить относительно просто;

• Если y известно, то f(x) вычислить практически невозможно.

В основу криптографической системы с открытым ключом RSA положена задача умножения и разложения простых чисел на множители, которая является вычислительно однонаправленной задачей.

Чтобы использовать алгоритм RSA, надо сначала сгенерировать открытый и секретный ключи, выполнив следующие шаги:

1. выбираются два различных случайных простых числа p и q;

2. вычисляется n как результат умножения p на q (n = p × q);

3. выбирается целое случайное число, которое назовем d (оно должно быть взаимно простым с m результатом умножения (р – 1) × (q – 1));

4. определяется такое число e, для которого является истинным следующее соотношение: (e × d) mod (m) =1 или e = (1 mod (m))/d.

Открытым ключом будут числа e и n, а секретным ключом – числа d и n.

Теперь, чтобы зашифровать данные по известному ключу {e, n}, необходимо сделать следующее:

• разбить шифруемый текст на блоки, каждый из которых может быть представлен в виде числа М(i) = 0, 1, …, n – 1;

• зашифровать текст, рассматриваемый как последовательность чисел М(i) по формуле С(i) = (М(i)e) mod n.

Чтобы расшифровать данные, используя секретный ключ {d, n}, необходимо выполнить следующие вычисления: М(i) = (С(i)d) mod n. В результате получится множество чисел М(i), которые представляют собой исходный текст.

Применим метод RSA для шифрования сообщения "ГАЗ".

Выберем p = 3 и q = 11.

Определим n = 3 × 11 = 33.

Найдем (p – 1) × (q – 1) = 20. Следовательно, в качестве d выберем любое число, которое является взаимно простым с 20, например d = 3.

Выберем число е. В качестве такого числа может быть взято любое число, для которого удовлетворяется соотношение (e × 3) mod 20 = 1, например 7.

Представим шифруемое сообщение как последовательность целых чисел в диапазоне 0…32. Пусть буква А изображается числом 1, буква Г – числом 4, а буква З – числом 9. Тогда сообщение можно представить в виде последовательности чисел 4 1 9. Зашифруем сообщение, используя ключ {7, 33}:

C1 = (4⁷) mod 33 = 16384 mod 33 = 16,

C2 = (1⁷) mod 33 = 1 mod 33 = 1,

C3 = (9⁷) mod 33 = 4782969 mod 33 = 15.

Шифртекст: "16 1 15".

Попытаемся расшифровать сообщение {16, 1, 15}, полученное в результате зашифрования по известному ключу, на основе секретного ключа {3, 33}:

М₁ = (16³) mod 33 = 4096 mod 33 = 4,

М₂ = (1³) mod 33 = 1 mod 33 = 1,

М₃ = (15³) mod 33 = 3375 mod 33 = 9.

Таким образом, в результате расшифрования сообщения получено исходное сообщение "ГАЗ".

Криптостойкость алгоритма RSA основывается на предположении, что исключительно трудно определить секретный ключ по известному, поскольку для этого необходимо решить задачу о существовании делителей целого числа. Данная задача является NР – полной и, как следствие этого факта, не допускает в настоящее время эффективного (полиномиального) решения. Более того, сам вопрос существования эффективных алгоритмов решения NР – полных задач является до настоящего времени открытым. В связи с этим для чисел, состоящих из 200 цифр (а именно такие числа рекомендуется использовать), традиционные методы требуют выполнения огромного числа операций (около 10²³). Время выполнения наилучших из известных алгоритмов разложения при n > 10¹⁴⁵ на сегодняшний день выходит за пределы современных технологических возможностей.