Механизм запоминания.

Компилятору нужны методы организации информации, способные быстро запоминать и выдавать информацию о большом числе различных объектов. Кроме того, в то время как число объектов, реально появляющихся в программе, может быть и велико(100 или 1000), число всех возможных объектов имеет порядок несравненно более высокий, большинство из возможных идентификаторов в данной программе не появляется.

Разберем использование для запоминания информации об объектах таблиц с прямым доступом. В такой таблице для каждого возможного объекта резервируется отдельная ячейка. В ней запоминается информация относительно этого объекта и нет необходимости запоминать в таблице его имя. Если число возможных объектов мало и для каждого объекта действительно можно выделить отдельную ячейку, то такая таблица – таблица с прямым достаточном – даёт очень быстрый механизм запоминания и извлекается информация об объектах. Однако в большинстве случаев идею применения таблицы с прямым доступом приходиться отвергнуть т.к размер таблицы был бы недопустимым, а большая часть её не использовалась. Например, число идентификаторов 1,133*10⁹.

Другой возможный метод запоминания – использование магазина. Когда встречается новый объект, его имя и указатель на информацию, относящуюся к этому объекту помещается в вершину магазина(стека). В этом случае размер таблицы пропорционален числу действительно встречающихся объектов, а новые объекты можно вставить очень быстро. Но извлечение информации об объекте требует просмотра магазина до тех пор, пока объект не будет обнаружен. Таким образом, в среднем поиск требует времени пропорционально числу объектов в магазине. Этот метод часто бывает удобен для небольшого числа объектов. Он имеет преимущество при компиляции языков с блочной структурой, т.к. кроме старого объявления переменной в таблицу можно поместить и новое. Когда блог закончен, все его объявления выталкиваются из магазина, а старые объявления переменных остаются.

Третий метод более быстрой – в применении дерева двоичного поиска. В дереве двоичного поиска у каждой вершины может быть левый прямой потомок и правый прямой потомок. Предполагается, что объекты данных можно линейно упорядочить некоторым отношением <, например, отношением «предшествовать в алфавитном порядке». Объекты запоминаются как метки в вершинах дерева, когда встречается первый объект, скажем 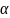1, порождается корень, который помечается 1. Если 2 следующий объект и 2< 1, то к дереву добавляется лист помеченный 2 и он остановится левым прямым потомком корня. Если 1< 2,то этот лист становится правым прямым потомком. Появление каждого нового объекта приводит к тому, что к дереву добавляются новый лист в такой позиции, что дерево всегда обладает свойством: пусть N – вершина дерева, помеченная . Если N имеет левое поддерево, содержащее вершину, помеченную , то , если N имеет правое поддерево с вершиной, помеченной , то .
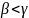