1.1 Теоретические сведения к практической работе №1
Для успешного решения задач, с использованием классического определения вероятности, необходимо знать основные формулы комбинаторики. Простейшие комбинации, использование которых необходимо знать: перестановки, сочетания, размещения.
Перестановки (от французского слова – permutation) – это комбинации, состоящие из одних и тех же элементов и отличающихся только порядком расположения элементов.
Формула для расчёта количества перестановок:
,
(1)
где n – общее количество элементов;
– факториал
числа n.
Факториал числа рассчитывается по формуле:
,
(2)
где n – положительное число, от которого вычисляется факториал.
Сочетания (от французского слова – combinasion) – это комбинации, составленные из n различных элементов по k элементам и отличающихся составом элементов.
Формула для расчёта количества сочетаний:
,
(3)
где n – общее количество элементов;
k – количество выбираемых элементов из n;
.
Формулу (3) применяют, когда порядок расположения выбранных элементов не важен.
Свойства сочетаний:
1)
;
2)
;
3)
;
4)
.
Размещения (от французского слова – arrangement) – это комбинации, составленные из n различных элементов по k элементам и отличающихся либо составом элементов, либо порядком расположения элементов.
Формула для расчёта количества размещений:
,
(4)
где n – общее количество элементов;
k – количество выбираемых элементов из n;
.
Формулу (4) применяют, когда порядок расположения выбранных элементов важен.
Свойства размещений:
1)
;
2)
;
3)
;
4)
.
1.2 Примеры решения задач к практической работе №1
Пример 1: В соревновании участвовало 8 команд. Сколько существует вариантов в распределении мест между ними?
Решение:
Ответ: 40320 варианта в распределении мест.
Пример 2: В полуфинале 8 команд, в финал попадает только три из них. Сколько существует вариантов выхода команд в финал?
Решение:
Ответ: 56 вариантов выхода трёх команд в финал.
Пример 3: В финале 8 команд. Разыгрываются три медали. Сколько существует вариантов в распределении медалей?
Решение:
Ответ: 336 вариантов в распределении медалей.
Пример 4: Вычислить значение выражения:
.
В данное выражение входят три размещения. Вычислим отдельно каждое размещение.
,
,
,
Подставим найденные значения в первоначальное выражение.
.
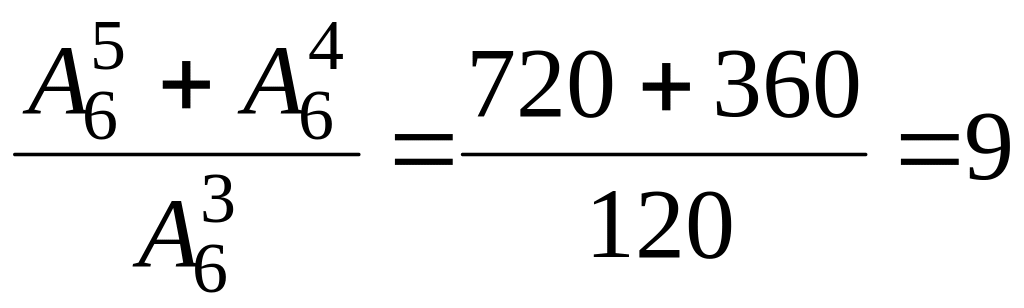Ответ: Значение выражения равно 9.
Пример 5: Решить уравнение:
Решение:
,
,
,
По свойству пропорции получаем:
,
,
,
,
,
,
.
Ответ: 9,10.
Пример 6: В шахматном турнире, где участники встретились между собой один раз, два шахматиста выбыли по болезни, успев сыграть по 3 партии каждый. Сколько шахматистов начали турнир, если было сыграно 84 партии?
Решение: Составим и решим уравнение:
,
,
,
,
,
,
,
,
.
Ответ: 15 шахматистов начали турнир.