2.4. Управление текущими издержками

2.4.4. Методы дифференциации издержек (метод максимальной точки и минимальной точки, графический метод, метод наименьших квадратов) для планирования

Для принятия управленческих решений и планирования, необходимо разделить или дифференцировать совокупные затраты на переменную и постоянную части. В теории и практике финансового менеджмента существуют 3 основных метода, позволяющих решить задачу дифференцирования затрат:

1. Максимальной и минимальной точки.

2. Графический.

3. Наименьших квадратов.

1. Максимальная и минимальная точки

Данный метод является наиболее простым с точки зрения практического применения. Он позволяет определить линейную зависимость между уровнем деловой активности и затратами на основе анализа наибольшей и наименьшей величины объема производства за период и связанные с ним затраты. Изменение в суммарных затратах между этими двумя уровнями делят на изменение в объеме и, таким образом, получают переменную часть суммарных затрат. Если любые затраты в общем виде представить формулой

y = a + bx,

где y – совокупные затраты; а – постоянные затраты; b – переменные затраты на единицу продукции; x – показатель, характеризующий уровень деловой активности (объем производства товаров в натуральных единицах измерения), то

где Δу – изменение совокупных затрат; Δх – изменение объема производства.

Для определения показателей в уравнении возьмем исходные данные из таблицы 2.3.

Таблица 2.3

Объем производства и расходы на электроэнергию

Месяцы	Объем производства, шт. (x)	Расходы на электроэнергию, руб. (y)
1 2 3 4 5 6 7 8 9 10 11 12	10 8 10 11 12 9 8 7 8 10 12 13	3750 3500 3700 3750 3800 3430 3350 3350 3420 3700 3800 3860
Итого:	118	43 410

Данные таблицы 2.3 показывают, что максимальный объем производства был достигнут в декабре, что соответствовало расходам в 3860 руб. Минимальный – в августе – 7 штук, на что было израсходовано 3350 руб. Следовательно, отклонение по объему – 6 штук, по расходам – 510 руб.

Тогда

Отсюда величину переменных затрат в максимальных и минимальных точках рассчитаем умножением ставки переменных затрат b на соответствующий объем производства х.

Переменные затраты в максимальной точке:

b_max = 85 · 13 = 1105.

В минимальной точке:

b_min = 85 · 7 = 595.

Теперь вычислим постоянную часть суммарных затрат в максимальной и минимальной точках, вычитая из общей суммы затрат переменные.

а_max = 3860 – 1105 = 2755.

а_min = 3350 – 595 = 2755.

Таким образом, линейную зависимость для данного примера выражают уравнением

y = 2755 + 85х,

т. е. изменяя объемы производства, можно получить суммарные затраты.

2. Графический метод

Данный метод заключается в перенесении всех данных о суммарных затратах на график в виде точек.

Затем проводят прямую линию суммарных затрат с помощью линейки, которую накладывают на все точки так, чтобы наилучшим образом аппроксимировать все множество точек.

Точка пересечения этой линии с осью ординат показывает постоянные издержки, в нашем примере это 2 755 руб. (рис. 2.6). Точки пересечения – это соответствия объема производства расходам на электроэнергию (линия ординат) исходя из данных таблицы 2.3.

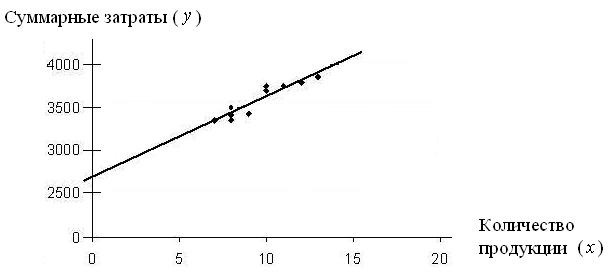
Рис. 2.6. Дифференциация затрат графическим методом

Тогда ставку переменных затрат из уравнения 1-го рассчитывают по следующей формуле:

– средние суммарные затраты за период; FC – постоянные затраты за период; – средний объем производства.

Линейную зависимость построим, исходя из 1-го уравнения:

у = 2755 + 83,4х.