2. Функция распределения Ферми-Дирака. Уровень Ферми. Влияние температуры на распределение Ферми-Дирака

 

Функция распределения Ферми-Дирака, описывающая распределение фермионов по состояниям, имеет следующий вид:

(4)

здесь E_F- химический потенциал системы фермионов, т.е. работа, которую необходимо затратить, чтобы изменить число частиц в системе на одну. В случае электронов величинаE_Fназываетсяэнергией Ферми или уровнем Ферми.

Рассмотрим вид функции Ферми-Дирака при температуре, стремящейся к абсолютному нулю. Как нетрудно видеть из формулы (4), для любой энергии частицы, большей энергии Ферми, экспонента в знаменателе стремится к бесконечности при , следовательно,f(Е)стремится к нулю. Это значит, что все энергетические состояния сЕ > E_Fсовершенно свободны при абсолютном нуле. ЕслиЕ < E_Fпри ,f(E)стремится к единице. Это значит, что все квантовые состояния с энергией, меньше энергии Ферми, полностью заняты электронами. Отсюда понятен физический смысл энергии Ферми как параметра распределения электронов по состояниям:энергия Ферми есть максимально возможная энергия электронов в металле при температуре абсолютного нуля. Энергетический уровень, соответствующий энергии Ферми, называетсяуровнем Ферми.

Вид функции распределения Ферми-Дирака при Т = 0Кпредставлен на рис. 2а. На рис. 2б показано распределение электронов по энергетическим уровням в зоне проводимости металла при этой же температуре.

Рис. 2. Функция распределения Ферми-Дирака (а) и распределение электронов в зоне проводимости металла при Т=0К (б)

Если Т  0К, то при энергии частицы, равной энергии Ферми, функция распределения Ферми-Дирака равна1/2. Это значит, что при любой температуре, отличающейся от абсолютного нуля, уровень Ферми заполнен наполовину. Вид функции Ферми-Дирака для двух различных температур показан схематически на рис. 3. Изменение характера распределения электронов по состояниям связано с тепловым возбуждением электронов. При этом часть электронов переходит в состояния с энергиями, большей энергии Ферми.

Соответственно часть состояний ниже уровня Ферми оказывается свободной. В результате функция f(E)"размыта" вблизи энергии Ферми. Тепловому возбуждению подвергается незначительная часть электронов, находящихся вблизи уровня Ферми. Функция Ферми-Дирака заметно отличается от вида, который она имела при абсолютном нуле, лишь при . Величина "размытия" пропорциональна температуре (рис. 3). Чем выше температура, тем более существенному изменению подвергается функция распределения.

Рис. 3. Функция распределения Ферми-Дирака при Т>0K

При условии

(5)

экспонента в знаменателе становится значительно больше единицы в формуле (4). В этом случае единицей можно пренебречь и распределение Ферми-Дирака преобразуется к виду

(6)

Выражение (6) совпадает по форме с функцией распределения Максвелла-Больцмана.

Вероятность того, что некоторый энергетический уровень с энергией Есвободен, т.е. занят дыркой, равна

(7)

Таким образом, функция распределения Ферми-Дирака для дырок аналогична функции распределения для электронов, если в ней изменить знаки показателей экспонент. Это хорошо согласуется с представлением о том, что дырки являются носителями положительного заряда.

Газ носителей заряда, подчиняющийся статистике Ферми-Дирака, называется вырожденным. Если носители заряда подчиняются статистике Максвелла-Больцмана, то они называютсяневырожденными.

\3. Функция плотности состояний электронов и дырок

Для определения числа частиц, имеющих энергию в заданном интервале, необходимо, кроме функции распределения , знать функцию плотности состояний . Эта функция описывает распределение уровней в соответствующих зонах и определяет число уровней, приходящихся на единичный интервал энергии. По определению

(8)

Здесь, как и раньше, dZ- число возможных состояний ансамбля частиц (число уровней) с энергией, заключенной в интервале отEдоE+dE. Функциюg(E)вычислим для кубического кристалла со сторонойL. Энергия электрона у дна зоны проводимости(Е(к) дать рисунок) приближенно может быть представлена в виде

(9)

здесь энергия дна зоны проводимости, - эффективная масса электрона у дна зоны проводимости,k- квазиимпульс электрона, - его компоненты. Согласно граничным условиям, компоненты квазиимпульса могут принимать только следующие дискретные значения энергии:

 

Каждому набору чисел n_x,n_y,n_zотвечает некоторое квантовое состояние (квантовый уровень). В пространстве волновых векторов каждому квантовому состоянию соответствует объем , гдеV- объем кристалла. Эти элементарные кубические ячейки займут в пространстве волновых чисел объем шара радиусомk, соответствующего максимально возможному значению модуля волнового вектора. Выделим шаровой слой, заключенный между двумя поверхностямиk=constиk+dk =const. Объем этого слоя составляет . Разделив этот объем на объем элементарной ячейки и умножив на 2, поскольку в каждом состоянии могут находиться по два электрона с противоположно направленными спинами, получим число состояний в объеме шарового слоя:

(10)

Согласно (9)

 

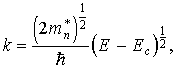
Подставляя значения k² иdkв формулу (10), получим

.

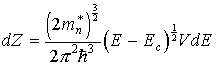Учитывая (8), получим окончательное выражение для плотности квантовых состояний электронов у дна зоны проводимости:

(11)

Энергию дырок у потолка валентной зоны можно записать также в виде параболического закона:

(12)

где E_v- энергия потолка валентной зоны, - эффективная масса дырки. Вычисления, аналогичные тем, которые были проведены выше для электронов, приводят к следующему выражению для функции плотности состояний дырок вблизи потолка валентной зоны:

(13)

Следует подчеркнуть, что формулы (11) и (13) справедливы только для состояний вблизи экстремумов энергии, т.е. у дна или потолка энергетической зоны. В средней же части зоны точный вид функции g(E) неизвестен. На рис. 4 схематически представлены зависимости плотности квантовых уровней вблизи дна зоны проводимости и потолка валентной зоны.

Рис. 4. Плотность уровней в зоне проводимости и в валентной зоне

Площадь заштрихованных областей пропорциональна числу уровней dZв интервале энергийdE