Глава 3 (окончание). Основы расчётов теплообменников системы охлаждения двс.

Принципиальная схема использования метода N– з для решения прямой и обратной задачи; определение средних температур теплоносителей; определение граничных условий по теплообмену и сопротивлению для различных теплоносителей.

3.3. Принципиальная схема использования метода n – з для

решения прямой и обратной задачи.

Рассмотрим упрощённо использование зависимостей з = f(N, S)для решения прямой и обратной задач расчёта ТО. В качестве примера выберем охладитель наддувочного воздуха (ОНВ).

Прямая задача.

Дано: Расходы теплоносителей, начальные температуры обоих теплоносителей, конечная температура горячего теплоносителя. Ради упрощения задачи значение коэффициента теплопередачи k также принимается известным (в реальной постановке вместо k задаются граничные условия по теплообмену).

Определить: Величину площади поверхности теплообмена (в реальной задаче определяются все конструктивные размеры).

Решение: 1. Вычисляется значение КПД ТО по формуле (2.8). Применительно к ОНВ на номинальном режиме:

2. Вычисляются значения энергоёмкостей теплоносителей, определяется, которая из них меньшая, и находится отношение меньшей к большей. Для ОНВ

3. Принимается возможная схема ТО (см. рис. 1.1). Для многоходового ТО определяется КПД одного хода. Например, для ОНВ по (3.25, 3.29)

4. Вычисляется значение N. Например, по (3.27, 3.31).

Принципиально возможно определение N с помощью графиков.

На рис. 3.4 дан пример такого определения N_х по известному КПД

одного хода и известному S для однократного перекрёстного тока.

При известном N_х значение N для всего теплообменника определяется

с учётом числа ходов по (3.28).

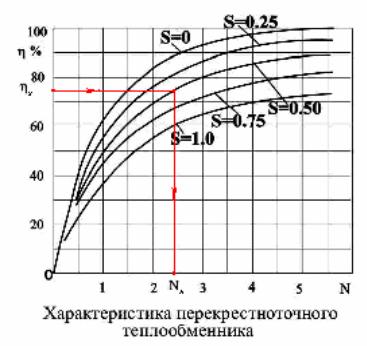
Рис.3.4. Схема определения Nх = f(зх, S) графическим путём в прямой задаче

5. Определяется искомая площадь поверхности по формуле

Обратная задача.

Дано: Расходы теплоносителей, их начальные температуры, известна площадь поверхности теплообмена, известна схема теплообменника, известно значение коэффициента теплопередачи k.

Определить: Значение конечных температур теплоносителей

Решение:

1. Вычисляются значения энергоёмкостей теплоносителей, определяется, которая из них меньшая по величине и находится отношение меньшей к большей (см. п. 2 прямой задачи).

2. Определяется значение N. В соответствии с (3.19) и применительно к ОНВ используется выражение.

Для многоходового теплообменника определяется

N_x=N/b_w

3. Вычисляется значение КПД ТО как функции N с использовани-

ем формул 3.20, 3.29, 3.32, 3.33 и аналогичных им. Аналогично пря-

мой задаче возможно использование графической зависимости, кото-

рое показано схематически на рис. 3.5. При этом для многоходовых

теплообменников таким образом вначале определяется КПД одного

хода с последующим вычислением КПД всего теплообменника по

формулам, учитывающим число ходов и схему взаимного течения те-

плоносителей в многоходовом теплообменнике. В частности, для мно-

гократного перекрёстного тока при общем противотоке это выполня-

ется по (3.23) и (3.24).

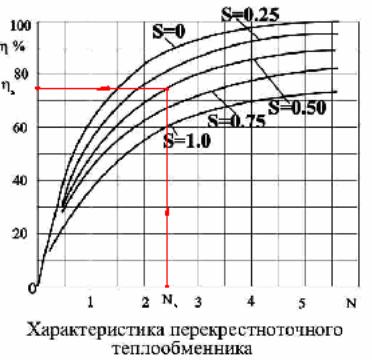
Рис.3.5. Схема определения зх=f(Nх,S) графическим путём в обратной задаче

Определяется конечная температура одного теплоносителя на основании (2.8), (2.11) или (2.12). В частности, для ОНВ конечная температура воздуха

T₂=T₁-з_вн (T₁-T_w1).

Конечная температура второго теплоносителя определяется на основании уравнения теплового баланса (3.7). Для ОНВ конечная температура воды определится из выражения

T_w2=T_w1+S(T₁-T₂).

В рассмотренных примерах исключён учёт сопротивления пучка по обоим теплоносителям, а граничные условия по теплообмену сведены к заданию значения коэффициента теплопередачи k. Кроме того, все особенности конструкции ПТ и собственно ОНВ сведены к величине площади поверхности теплообмена F. Учёт названных выше и некоторых других исключённых в рассмотренных примерах элементов расчёта значительно усложняет алгоритм реальной расчётной методики. Тем не менее, рассмотренные примеры важны для принципиального понимания действия одного из наиболее важных расчётных компонентов полноразмерных расчётных методик. Далее рассмотрим содержание дополнительных элементов расчётов ТО, которые обязательно используются при решении расчётных задач без упрощений.