4.2.Полные алгоритмы решения прямой и обратной задач
Аналитическая основа алгоритмов
Для получения компактных алгоритмов решения прямой и обратной задач основная система уравнений (3.1)…(3.16) должна быть преобразована с получением удобных расчётных формул и уравнений. С этой целью на основании совместного решения системы (3.1)…(3.7) получаем выражение для определения коэффициента теплопередачи в функции коэффициентов теплоотдачи и термического сопротивления стенки
Далее это уравнение удобно привести к безразмерному виду. Для этого левую и правую части уравнения умножаем на дробь Wmin / F . Получим
При дальнейшем преобразовании полученного уравнения примем, что для ОНВ на номинальном режиме работы Wmin = GCp . Число Рейнольдса представим с учётом (3.8) в виде
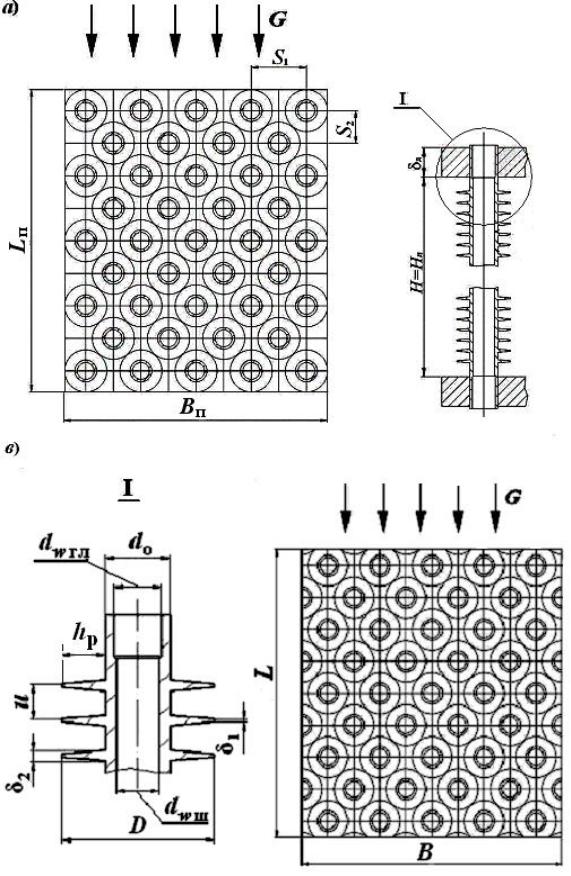
Рис. 4.2 Геометрические параметры трубки и трубного пучка:
а) конструктивные размеры и конструктивная структура трубного пучка; в) расчетные размеры и расчётная структура пучка
Одновременно принимаем во внимание, что
Коэффициент теплоотдачи со стороны воздуха на основании (3.10) представим выражением
После подстановки (4.3) и (4.4) в (4.2) и ряда преобразований получим основное уравнение компактного алгоритма решения обратной задачи
где Сi – комплексы, постоянные или мало изменяющиеся при решении рассматриваемых задач; все комплексы имеют размерность «метр» (м);
Воспользуемся далее уравнением (3.15) для выражения длины пучка в функции величины воздушного сопротивления пучка. При этом ради упрощения последующих выражений принимаем, что сопротивление определяется только газодинамическими потерями в пучке (допустимо для решения прямой задачи; в обратной задаче учитываются все виды влияния на величину падения давления). Тогда
L = C1 Re-m, (4.7)
где
Подставив (4.8) в (4.5) получим основное уравнение компактного алгоритма решения прямой задачи
Уравнение (4.5) удобно решается относительно N в условиях обратной задачи. Уравнение (4.9) удобно решается относительно числа Re в условиях прямой задачи. Это способствует организации компактных алгоритмов решения обоих задач. Далее для решения прямой задачи удобно располагать выражением для определения ширины пучка при известной длине и заданной максимальной скорости воды в трубках wwmax. Такое выражение может быть получено из уравнения расхода по воде для пучка ОНВ (3.9) с учётом выражения для φw :
Выражение для определения высоты трубного пучка H можно получить из уравнения расхода для воздушного потока (3.8), решаемого совместно с выражением для вычисления числа Re и выражением для определения коэффициента стеснения воздушного потока ц. При условии, что известна ширина пучка B и известно число Re
Таким образом, после проведения преобразований основной системы уравнений, была получена система выражений (4.5…4.11), которая, при отображении тех же физических связей, что и исходная система, более удобна для построения удобных методик решения, ход которых изложен ниже.
Алгоритм решения прямой задачи
Рассмотрим решение прямой задачи расчёта ОНВ в реальной постановке, без существенных упрощений.
Дано: Расход воздуха G, давление воздуха перед ОНВ P1, воздушное сопротивление ОНВ P1, температура воздуха перед ОНВ T1, температура воздуха за ОНВ T2, расход воды через ОНВ Gw, температура воды перед ОНВ Tw1. Задан также вид, тип ПТ, а также значения определяющих размеров ПТ и особенности её конструкции.
Определить: Размеры пучка ОНВ Lп,Bп,Hп.
Решение.
1. Дополнительно к располагаемым исходным данным следует принять предельно допустимое значение скорости воды в трубках ОНВ ww max, которое выбирается в зависимости от материала трубок и качества воды.
2. Вычислить все геометрические параметры ПТ, используемые в расчётах.
3. Определить константы частных критериальных зависимостей для определения граничных условий по теплообмену и сопротивлению.
4. Вычислить значение КПД ОНВ з.
5. Вычислить значения водяных эквивалентов теплоносителей и определить их отношение S.
6. Принять возможную схему взаимного течения теплоносителей через ОНВ и задаться числом ходов по воде bw.
7. Вычислить значение N=f (з, S, bw) с использованием (3.19…3.28).
8. Определить средние температуры теплоносителей и найти значения коэффициентов вязкости и теплопроводности теплоносителей.
9. Вычислить значения С-комплексов уравнения (4.9) по (4.6) и (4.8) и решить это уравнение относительно числа Re.
10. Найти теоретические размеры пучка по (4.7), (4.10), (4.11).
11. На основании полученных размеров определить значение числа продольных и поперечных рядов пучка Z1 и Z2 соответственно. Округлить полученные значения до целых чисел.
12. По округлённым значениям Z1 и Z2 определить конструктивные размеры пучка.
13. Для конструктивных размеров пучка сформировать условие обратной (поверочной) задачи и решить её, уточнив теплотехнические параметры спроектированного ОНВ. При большом отклонении параметров от заданных величин производить коррекцию размеров и повторять обратные расчёты до получения приемлемого решения.
При анализе результатов решения и при необходимости изменить пропорции размеров фронта ОНВ рекомендуется изменять их путём коррекции исходных значений числа ходов по воде bw. При изменении bw будет увеличиваться высота пучка с одновременным уменьшением ширины или наоборот, в зависимости от характера изменения bw. Площадь фронта в этом случае сохраняется практически постоянной. С целью коррекции этих же размеров можно допустить некоторое изменение задаваемой скорости воды в приемлемых пределах. При этом следует учитывать, что уменьшение скорости воды увеличивает размеры ОНВ, и что это влияние нелинейное. Длина пучка однозначно зависит от КПД ОНВ и его воздушного сопротивления, а также от вида и типа ПТ. При сохранении этих параметров она не может быть скорректирована.
Алгоритм решения обратной задачи
Решение обратной (поверочной) задачи без существенных упрощений и схематизации может быть выполнено на основе следующего алгоритма.
Дано: Расход воздуха G , давление воздуха перед ОНВ P1, температура воздуха перед ОНВ T1, расход воды через ОНВ Gw, температура воды перед ОНВ Tw1. Известны габаритные размеры пучка ОНВ Lп, B п, H п и число ходов по воде bw. Задан также вид, тип ПТ, а также значения определяющих размеров ПТ и особенности её конструкции.
Определить: Температуры воздуха и воды за ОНВ T2 и Tw2 , воздушное сопротивление ОНВ Д P, сопротивление по воде Д Pw.
Решение.
1. Вычислить все геометрические параметры ПТ, используемые в расчётах.
2. Задаться предварительно значением КПД ОНВ з (в первом приближении).
3. Определить значения водяных эквивалентов теплоносителей и их отношение S.
4. Вычислить в первом приближении значение N =f (з, S, bw) с использованием (3.19…3.28).
5. Определить значения конечных и средних температур теплоносителей в первом приближении, найти соответствующие значения коэффициентов вязкости и теплопроводности теплоносителей.
6. Определить константы частных критериальных зависимостей для определения граничных условий по теплообмену и сопротивлению.
7. Вычислить значения С-комплексов уравнения (4.5) с использованием (4.6).
8. Найти число Рейнольдса по формуле
9. Определить значение N во втором приближении по (4.5).
10. Вычислить значение КПД ОНВ з во втором приближении с использованием
(3.20…3.24).
11. Определить значение температуры воздуха за ОНВ
T2 = T1 з (T1 Tw1 ) .
12. Определить значение температуры воды за ОНВ
Tw2 = Tw1 + S(T1 T2 ) .
13. Сравнить полученное значение температуры воздуха за ОНВ с установленным ранее на основе принятого в первом приближении значения КПД ОНВ з (см. п.5). Если разность полученного и принятого значений температур воздуха за ОНВ, превышает допустимую погрешность, заменить КПД, принятый в первом приближении, значением, полученным во втором приближении (по п. 10). После этого повторять расчёт, начиная п.2 и заканчивая п. 13, до обеспечения приемлемой точности.
14. Определить полное воздушное сопротивление ОНВ с учётом газодинамических потерь и замедления потока с использованием (3.12…3.15).
15. Определить сопротивление ОНВ по воде по (3.64).
Поверочный расчёт ОНВ по своей специфике может и должен быть более точным, чем прямой расчёт, в котором неизбежны округления полученных размеров. Соответственно при его реализации уместно использование более точных формул или учёт большего числа параметров при использовании тех же формул, что и в прямом расчёте. Как правило, обратный расчёт всегда должен сопровождать выполнение прямого расчёта, если этого требует принятая точность вычислений.