БОЛЬШОЙ набор материала по курсу / 2.3.Электростатический анализ p-n перехода

Электростатический анализ p-n перехода

Электростатический анализ p-n перехода представляет интерес прежде всего потому, что позволяет получить информацию о заряде и поле в слое объемного заряда. Он необходим также и для исследования вольтфарадной характеристики диода.

Анализ перехода основан на решении уравнения Пуассона для потенциала :

,

где плотность заряда выражена как функция плотностей электронов, дырок, доноров и акцепторов. Плотности электронов и дырок в слое объемного заряда могут быть выражены, в свою очередь, как гиперболические функции потенциала

,

где

.

Такое нелинейное дифференциальное уравнении второго порядка не имеет аналитического решения. Однако при некоторых упрощающих предположениях решение этого уравнения является простым и наглядным. Первым таким предположением является допущение о том, что область объемного заряда представляет собой полностью обедненную область, т.е. в ней нет подвижных носителей тока (электронов и дырок), а смежные с ней области полупроводников n и p типа являются нейтральными.

1. Приближение полного обеднения слоя ОПЗ

Это приближение предполагает, что обедненная область вблизи металлургической границы имеет четкие границы между полностью обедненной областью перехода, в которой нет подвижных носителей, и квазинейтральной областью. В нейтральной области вне слоя объемного заряда плотность подвижных носителей почти равна плотности легирующей примеси.

Это приближение реально обосновано тем обстоятельством, что плотность подвижных носителей в полупроводнике экспоненциально зависит от разности энергий между уровнем Ферми и краями запрещенной зоны. Столь сильная зависимость концентрации подвижных носителей от разности энергетических уровней приводит к тому, что в слое объемного заряда доминирует заряд ионизованных атомов примеси. В однородно легированных полупроводниках плотность заряда будет постоянной.

В процессе анализа будем предполагать p-n переход резким и введем две неизвестных величины, а именно, ширину слоя объемного заряда для p – области, x_p, и ширину слоя объемного заряда для n – области, x_n. Сумма этих двух параметров есть общая ширина слоя объемного заряда w:

.

Зная профиль плотности заряда мы можем вычислить напряженность электрического поля в переходе и распределение потенциала в нем.

Но первое соотношение между неизвестными x_p и x_n и шириной ОПЗ можно получить из равенства положительных и отрицательных объемных зарядов. Это равенство должно соблюдаться, поскольку в квазинейтральных областях напряженность электрического поля должна равняться нулю. Второе соотношение между размерами слоев объемного заряда в p и n областях можно получить, связав ширину слоя объемного заряда с величиной приложенного к переходу напряжения. Тогда из полученных соотношений можно найти x_p и x_n.

2 Расчет плотности заряда

Величина плотности объемного определяется суммой концентраций зарядов, созданных дырками, электронами и ионами доноров и акцепторов. Если пренебречь зарядом, созданным подвижными носителями, то останется только сумма плотностей зарядов ионов:

На рисунке приведено распределение плотности заряда в переходе при обратом смещении в 5 вольт (толстая линия) и при нулевом смещении (тонкая линия). Плотность заряда измеряется в Кулонах/см³.

Fig.1 График распределения плотности заряда в переходе при -5 вольт и при 0 вольт. Слева p-область с концентрацией примесей N_a = 10¹⁶ cm^-3, а справа n-область с концентрацией доноров N_d = 2 x 10¹⁶ cm^-3

Плотность объемного заряда для различных областей диода с резким распределением примесей дается следующими соотношениями:

(1a)

(1b)

(1c)

(1d)

3. Расчет напряженности электрического поля

Из уравнения Пуассона следует уравнение Гаусса для напряженности электрического поля, созданного зарядом в диэлектрической среде:

(2)

Видно, что поле линейно зависит от координаты. Постоянную интегрирования можно найти из условия, что напряженность поля на обоих концах обедненной области и при -x_p и при x_n равна нулю. Это следует из условия электронейтральности областей, лежащих за слоем объемного заряда. А поскольку исходными материалами для перехода служили электронейтральные полупроводники p и n- типа, то отсюда же следует равенство положительных и отрицательных зарядов в ОПЗ.

В качестве примера на рисунке приведено распределение поля в ОПЗ при двух напряжениях на переходе: -5 вольт (толстая линия) и 0 вольт (тонкая линия).

Fig.2 Electric field in a p-n junction at -5 Volt bias (thick line) and at 0 Volt bias (thin line) (N_a = 10¹⁶ cm^-3 and N_d = 2 x 10¹⁶ cm^-3)

Максимальное значение напряженности электрического поля имеет место при x = 0 и может быть определено интегрированием уравнения Гаусса либо от x_p до 0, либо от x_n до 0:

Из данного уравнения следует, что

Последнее уравнения является по сути условием равенства объемных зарядов ионов доноров и акцептов в ОПЗ. Используя уравнение

можно получить, что

и

4. Расчет потенциала в переходе.

Распределение потенциала в полупроводнике можно найти из решения уравнения Пуассона

Поскольку поле в ОПЗ линейно зависит от координаты, то зависимость потенциала от координаты после интегрирования будет параболической. На рисунке приведен пример распределения потенциала в переходе при ранее выбранных параметрах (5 вольт и 0 вольт).

Fig. 3 Potential in a p-n junction at -5 Volt bias (thick line) and at 0 Volt bias (thin line) (N_a = 10¹⁶ cm^-3 and N_d = 2 x 10¹⁶ cm^-3)

Разность потенциалов между выводами перехода должна равняться разности между высотой потенциально барьера перехода и приложенным напряжением. Это условие дает второе соотношение, связывающее x_p и x_n, а именно:

5. Ширина слоя объемного заряда

Подставляя в последнее уравнение значения x_p и x_n, вычисленные ранее через концентрации примесей и полную ширину перехода, получим:

И подставляя теперь ширину перехода в формулы для x_p и x_n, получим:

6. Энергетические диаграммы

Энергетические диаграммы перехода приведены на рисунке

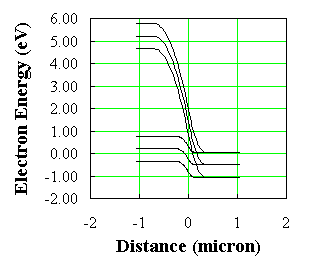
Fig. 4 Energy band diagram of a p-n junction at -5 Volt bias (upper set of curves) and at 0 Volt bias (lower set of curves)

© Bart J. Van Zeghbroeck, 1996, 1997

Шуренков В.В.

суббота, 5 октября 2002 г.