5.Переменный ток. Мощность переменного тока.

Установившиеся вынужденные электромагнитные колебания можно рассматривать как протекание в цепи, содержащей активные сопротивления, индуктивности и электрические емкости, переменного тока, обусловленное переменным напряжением U=U_mCos(t). Сила тока в цепи (на участке цепи): i(t)=I_mCos(t-). Характерной особенностью переменного тока является наличие разности фаз между напряжением и током .

Мощность переменного тока

Мгновенное значение мощности переменного тока на участке цепи равно произведению мгновенных значений напряжения и силы тока:

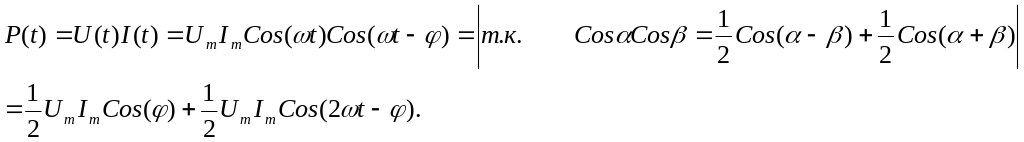Практический интерес представляет не мгновенное значение мощности, а её среднее значение за период колебаний T. Учитывая, что:

получим:

Величины I_g=I_m/2, U_g=U_m/2 называются действующими (эффективными) значениями тока и напряжения. Они же являются среднеквадратичными за период колебаний значениями тока, напряжения и для гармонически изменяющихся токов, напряжений связь между амплитудными значениями и ими оказывается таковой. Тогда среднее значение мощности переменного тока: равна произведению действующих значений тока и напряжения, и косинуса разности фаз между напряжением и током ( Cos - коэффициент мощности). На практике всегда стремятся увеличить Cos , наименьшим допустимым значением которого для промышленных установок составляет 0,85.

Все амперметры и вольтметры при измерении переменного тока показывают нам действующие значения тока и напряжения.

Расчет цепей переменного тока.

1. Пусть цепь состоит только из источника гармонического напряжения U=U_mCos(t) и активного сопротивления R. Т.е. R0, L=0, C=. Тогда из (3) §5 I_m=U_m/R, амплитудные ( и действующие) значения тока и напряжения связаны между собой аналогично как для цепи постоянного тока (закон Ома). Полное сопротивление цепи Z=R, Cos()=1, 1.щыением и тожения, и косинуса разности фаз между токоми оказывается таковой. чение за период колебаний. 00000000000000000000

2. Пусть цепь состоит только из источника гармонического напряжения U=U_mCos(t) и индуктивности L. Т.е. R=0, L0, C=. Тогда из (3) §5 I_m=U_m/(L). Полное сопротивление цепи Z=L, Cos()=0,  = /2, 0. Естественно, по аналогии с законом Ома, назвать X_L=L индуктивным сопротивлением. щыением и тожения, и косинуса разности фаз между токоми оказывается таковой. чение за период колебаний. 00000000000000000000

3. Пусть цепь состоит только из источника гармонического напряжения U=U_mCos(t) и конденсатора емкости С. Т.е. R=0, L=0, C0. Тогда из (3) §5 I_m=U_mС). Полное сопротивление цепи Z=1/C, Cos()=0,  = -/2, 0 . Естественно, по аналогии с законом Ома, назвать X_C=1/C емкостным сопротивлением цепи. щыением и тожения, и косинуса разности фаз между токоми оказывается таковой. чение за период колебаний. 00000000000000000000

4. Если цепь состоит из источника гармонического напряжения U=U_mCos(t) и последовательно соединенных активного сопротивления R, индуктивности L, емкости С. Т.е. R0, L0, C0. Тогда из (3) §5 I_m=U_m/Z. Полное сопротивление цепи , а величина X=X_L-X_C называется реактивным сопротивлением цепи. щыением и тожения, и косинуса разности фаз между токоми оказывается таковой. чение за период колебаний. 00000000000000000000

Если в некоторой электрической цепи активные сопротивления R, индуктивности L, емкости С соединены более сложным образом и во всех ветвях этой цепи имеют место гармонические напряжения и протекают гармонические токи (изменяющиеся по законам синуса или косинуса) существует удобный и эффективный метод расчета называемый методом комплексных чисел или метод Хевисайда. Для понимания этого материала необходимо знание простейших свойств комплексных чисел:

, здесь z – комплексное число, x=Re(z) – его действительная часть, y=Im(z) – его мнимая часть, i – мнимая единица (i²= - 1),  - модуль комплексного числа,  - аргумент комплексного числа, и . Формула Эйлера: .

Запишем гармонически изменяющееся напряжение в комплексной форме:

, здесь - комплексная амплитуда напряжения, e^it – осциллирующий множитель. Комплексная амплитуда Û содержит в себе информацию о действительной амплитуде напряжения U_m и о начальной фазе φ_U. Аналогично комплексная амплитуда гармонически изменяющегося тока:

Рассмотрим в цепи переменного тока произвольный блок, содержащий активные сопротивления, емкости и индуктивности. Отношение комплексной амплитуды напряжения к комплексной амплитуде тока называется импедансом блока Z:

, здесь φ=φ_U-φ_I – фазовый сдвиг напряжения по отношению к току. Наличие таких сдвигов является характерной особенностью цепей переменного тока. Таким образом, модуль импеданса определяет отношение действительных амплитуд напряжения и тока, а аргумент импеданса определяет фазовый сдвиг напряжения и тока.

Для расчета участка цепи переменного тока необходимо предварительно заменить сопротивления на соответствующие импедансы (комплексные сопротивления) следующим образом:

Затем необходимо получить формулу импеданса участка цепи используя правила сложения как для цепей постоянного тока. Импеданс последовательного соединения элементов равен сумме импедансов этих элементов: . Обратный импеданс параллельного соединения элементов равен сумме обратных импедансов этих элементов: . Получив формулу импеданса цепи, определяют его действительную и мнимые части, затем – его модуль и аргумент. По найденному модулю устанавливают связь между действительными амплитудами ( или действующими значениями) тока и напряжения на участке цепи, а аргумент определяет фазовый сдвиг между напряжением и током.

Пример:

В качестве примера вновь рассмотрим цепь состоящую из активного сопротивления R, конденсатора емкостью С, соленоида с индуктивностью L соединенных последовательно.

. Модуль импеданса цепи:

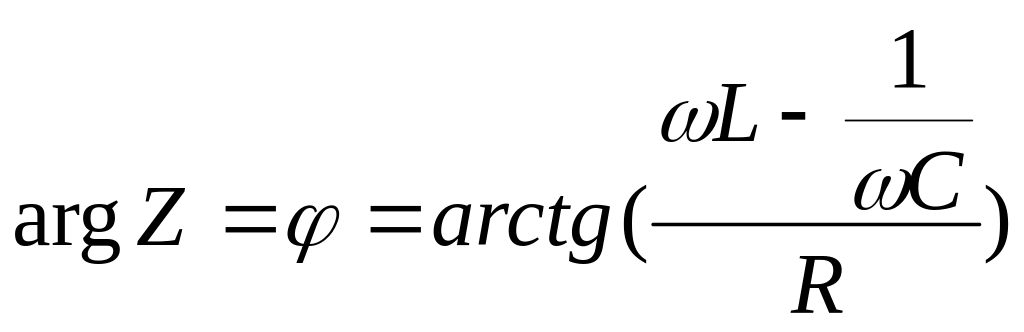, аргумент импеданса цепи равный разности фаз между током и напряжением: . Этот фазовый сдвиг может быть как в сторону опережения, так и в сторону запаздывания, в зависимости от соотношения между L и C..Таким образом, действительные амплитуды тока и напряжения связаны между собой соотношением:

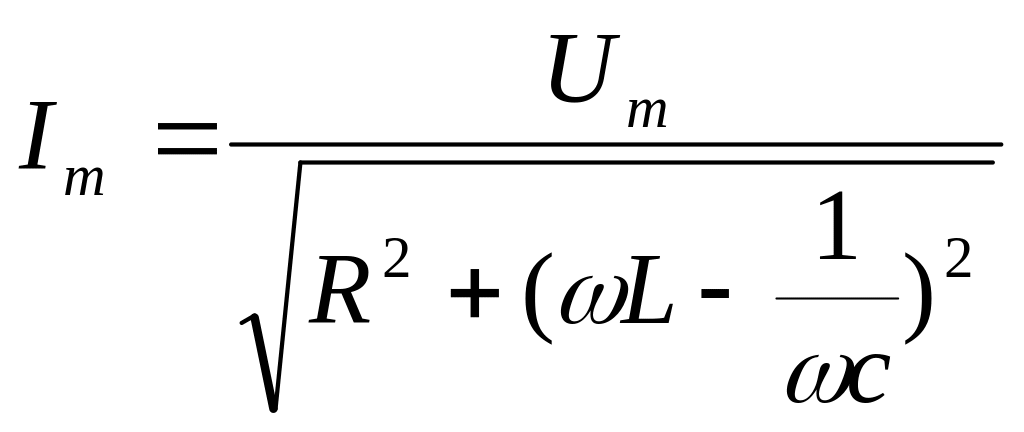
Для расчета сложных цепей переменного тока применяются также правила Кирхгофа. Формальная методика применения этих правил ( в частности правил знаков) аналогична цепям постоянного тока. Но вместо постоянных токов, напряжений и ЭДС используют комплексные амплитуды этих величин, вместо сопротивлений – импедансы.