Глава I.

1.Элементарный заряд. Закон сохранения заряда. Закон Кулона. Напряженность электрического поля. Напряженность поля точечного заряда. Принцип суперпозиции полей.

1. Заряд всех элем. частиц одинаков по абсолютной величине, его назыв. элем. зарядом. Положит. элем. заряд обозн. е. К числу элем. частиц принадл.: электрон (-е), протон (+е), нейтрон. Закон сохранения заряда: алгебраич. сумма электрич. зарядов любой замкнутой системы остаётся неизменной, какие бы процессы не происходили внутри этой системы. Электрич. заряд – величина релялятивистски инвариантная, т.е. не зависит от С.О., а значит не зависит от того, движется этот заряд или покоится. Закон Кулона: сила взаимодействия между двумя неподвижными точечными зарядами и обратнопропорц. квадрату расстояния между ними. ε₀ =8,85*10^-12 Ф/м

F=kq₁q₂/r² k=1/4πε₀

Всякий заряд изменяет свойства окружающего его пространства – создаёт в нём электрич. поле. Напряжённость электрич. поля в данной точке есть физ. величина, опред. силой, действ. на ед. положит. заряд, помещённый в эту точку поля: E=F/q₀. Напряжённость поля точечного заряда: E=1/4πε₀*q/ r² Напряжённость вектора Е совпадает с направлением силы, действующей на положит. заряд. Т.к. F=∑Fi то Е=∑Еi – принцип суперпозиции электр. полей, согласно которому напряж. Е результ. поля, создаваемого системой зарядов, равна геом. сумме напряж. полей, создаваемых в данной точке каждым из зарядов в отдельн.

2.Линии напряженности. Поток вектора напряженности. Теорема Гаусса и ее применение к расчету напряженности полей ( поля бесконечной однородно заряженной плоскости, поле двух разноименно заряженных параллельных плоскостей, поля объемно заряженного шара).

2. Графич. электрич. поле изобр. с помощью линий напряж. – линий, касат. к которым в каждой точке совпадают с направлением вектора Е. Число линий напряж., пронизывающих ед. площади поверхности, равно модулю вектора Е. Тогда число линий напряж. прониз. элем. площадку dS, нормаль n которой образует угол α с Е, равно EdScosα=E_ndS, где E_n-проекция Е на нормаль n. dФ_Е=E_ndS – поток вектора напряж. через площадку dS. Для произвольной замкнутой поверхн. S поток Е через эту поверхность Т.к. Е=∑E_i то Теорема Гаусса: поток вектора напряж. электрич. поля в вакууме сквозь произв. замкн. поверхн. равен алгебр. сумме заключённых внутри этой поверхн. зарядов, делённой на ε_0.

Поле бесконечной однородно заряженной пластинки: Е=σ/2ε₀ где σ=dq/dS – заряд приходящийся на ед. поверхности.

Поле двух параллельно разноимённо заряженных плоскостей: Е= σ/ε₀–между плоск., а вне Е=0. Поле объёмно заряженного шара: вне шара Е=1/4πε₀*q/r² (r>=R), внутри Е=1/4πε₀*q/R³*r` (r`<=R), R- радиус шара.

3.Работа сил электрического поля при перемещении заряда. Циркуляция вектора напряженности.

3. Если в электрич. поле точечного заряда q из точки 1 в точку 2 вдоль производной траектории перемещается другой точечный заряд q₀, то сила, приложенная к заряду, совершает работу. Работа силы F на элем. перемещ. dl: dA=Fdlcosα=1/4πε₀*qq₀/r²dlcosα

dlcosα=dr. Работа при перемещении заряда q₀ из точки 1 в 2

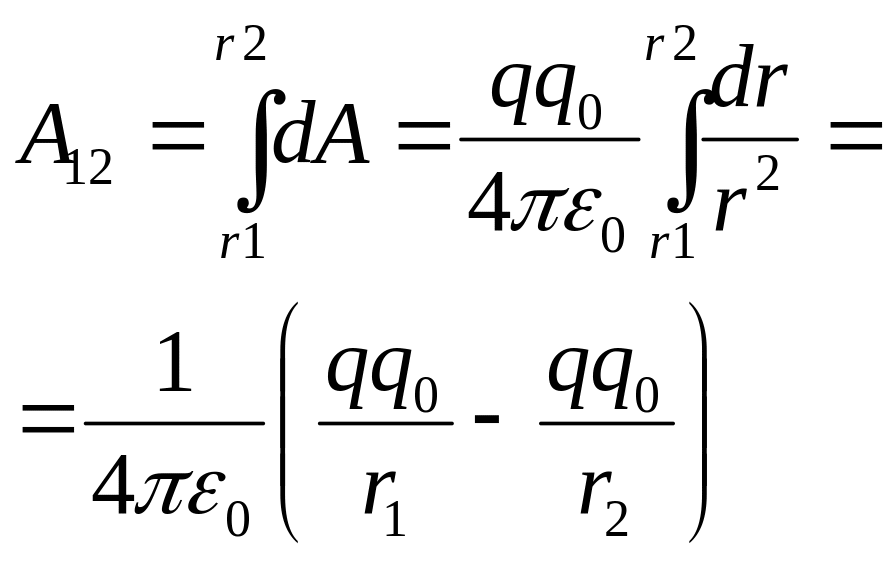
не зависит от траектории перемещения, а опред. только положениями нач. и конеч. точек. Следовательно, электрич. поле точечного заряда является потенциальным, а электрич. силы – консервативными. Работа по замкнутому контру: Если в качестве заряда, переносимого в электрич. поле, взять единичный точечный положительный заряд, то элем. работа сил поля на пути dl равна Edl=E_ldl, где E_l=Ecosα – проекция вектора Е на направление элем. перемещения. Тогда - циркуляция вектора напряж. Следовательно, циркуляция вектора напряж. электрич. поля вдоль любого замкнутого контура равна нулю.