23. Высотные геодезические сети.

Высотная (нивелирная) геодезическая сеть создается методом геометрического нивелирования.

Используется для геодезической съемки фасадов зданий, а также любых рукотворных и нерукотворных объектов, имеющих множество контрольных точек с разной высотой.

Высотная геодезическая сеть также как и плановая, подразделяется на сеть государственную, сеть сгущения и съёмочную сеть.

Государственная высотная геодезическая сеть – это нивелирная сеть 1, 2, 3 и 4 классов. При этом сети 1 и 2 классов являются высотной основой, с помощью которой устанавливается единая система высот на всей территории страны.

На линиях 1, 2, 3 и 4 классов закладывают вековые, фундаментальные, грунтовые, скальные, стенные и временные реперы.

25. Прямая геодезическая задача

26. Обратная геодезическая задача

Геодезическая задача – математического вида задача, связанная с определением взаимного положения точек земной поверхности и подразделяется на прямую и обратную задачу.

П рямой геодезической задачей (ПГЗ) называют вычисление геодезических координат - широты и долготы некоторой точки, лежащей на земном эллипсоиде, по координатам другой точки и по известным длине и дирекционному углу данного направления, соединяющей эти точки.

Обратная геодезическая задача (ОГЗ) заключается в определении по геодезическим координатам двух точек на земном эллипсоиде длины и дирекционного угла направления между этими точками.

В зависимости от длины геодезической линии, соединяющей рассматриваемые точки, применяются различные методы и формулы, разработанные в геодезии. По размерам принятого земного эллипсоида (см. Эллипсоид Красовского) составляются таблицы, облегчающие решение геодезических задач и рассчитанные на использование определённой системы формул.

Для определения координат точки в прямой геодезической задаче обычно применяют формулы: 1) нахождения приращений:

2) нахождения координат:

В обратной геодезической задаче находят дирекционный угол и расстояние:

1) Вычисляют румб по формуле:

2) Находят дирекционный угол в зависимости от четверти угла:

четверти:	Первая четверть	Вторая четверть	Третья четверть	Четвертая четверть
знак приращения	+X, +Y	-X, +Y	-X, -Y	+X, -Y
диреционный угол	a = r	a = 180 - r	a = 180 + r	a = 360 - r

3) Определяют расстояние между точками:

  

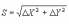
Геодезическая задача в том и другом виде возникает при обработке полигонометрии и триангуляции, а также во всех тех случаях, когда необходимо определить взаимное положение двух точек по длине и направлению соединяющей их линии или же расстояние и направление между этими точками по их геодезическим координатам. В ряде случаев геодезические задачи решают в пространственных прямоугольных координатах по формулам аналитической геометрии в пространстве. В этих случаях вместо длины и дирекционного угла, соединяющей две точки, используют длину и пространственные компоненты направления прямой линии между этими точками.