4 . Математическое описание случайных погрешностей

Выше отмечалось, что измеряемая величина, содержащая случайную погрешность, должна рассматриваться как случайная величина. Напомним, что наиболее общей характеристикой непрерывной случайной величины Х является плотность распределения ее вероятности, которая определяется как

, (2.1)

где dF(x) — вероятность значений случайной величины х в интервале dх.

Кроме этого используется функция распределения вероятностей случайной величины

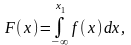(2.2)

которая выражает собой вероятность того, что случайная величина находится в интервале от – ∞ до некоторого значения, меньшего x₁.

Функция распределения любой случайной величины является неубывающей функцией, определенной так, что F(–∞) = 0, а F(+∞) = l. Вероятность того, что случайная величина Х примет значение в интервале между x₁ и x₂, равна

(2.3)

В практике электрорадиоизмерений чаще всего имеют дело с нормальным и равномерным распределениями.

Случайная величина Х распределена нормально, если ее плотность вероятностей имеет вид

(2.4)

где σ – среднее квадратическое отклонение (CКО), m = M[X] – математическое ожидание.

4.1 Оценка случайных погрешностей прямых равноточных измерений

Случайные погрешности проявляются при многократных наблюдениях измеряемой величины в одинаковых условиях. Их влияние на результат измерения надо учитывать и стремиться по возможности уменьшать.

К оценкам случайной величины, получаемым по статистическим данным, предъявляются требования состоятельности, несмещенности и эффективности. Оценка параметра Q считается состоятельной, если Ō (Q₁, Q₂, …. О_n)→Qист, при п → ∞, несмещенной, если М[Ō] = Qист, эффективной, если D[Ō] = min. Здесь Q_i – результат i-тогo наблюдения, п – число наблюдений.

Способы нахождения оценок конечного ряда наблюдений и показатели их качества зависят от законов распределения.

Для нормального распределения, а если поступиться эффективностью оценки, то и для всех симметричных распределений, в качестве оценки математического ожидания ряда равноточных наблюдений принимают среднее арифметическое ряда наблюдений

(2.5)

При п → ∞, если отсутствует систематическая погрешность, Ō→Qист. Разность v_i = Q_i – Ō, представляет собой случайную погрешность при i-том наблюдении. Она может быть положительной и отрицательной.

Среднее арифметическое независимо от закона распределения обладает следующими свойствами:

(2.6)

В качестве оценки дисперсии берется дисперсия отклонения результата наблюдения

(2.7)

а в качестве оценки СКО результата наблюдения –

(2.8)

Широко пользуются понятием максимальной погрешности, под которым понимают закон трех сигм. Так как на практике число измерений не превышает нескольких десятков, то появление погрешности, равной , маловероятно. Поэтому погрешность считается максимально возможной случайной погрешностью. Погрешности больше считаются промахами и при обработке результатов измерений не учитываются. Схема обработки результатов измерения с многократными наблюдениями приведена на рис. 2.1.

Рис. 2.1. Схема обработки результатов измерения