3. Результати моделювань

Була проведена наступна серія експериментів для встановлення впливу різних параметрів руху об’єкта та інтегрування на похибку БСО:

1. Похибки БСО в залежності від кроку інтегрування

2. Похибки БСО в залежності від частоти вимушених коливань

3. Похибки БСО в залежності від амплітуди коливань

В кінці було виведено теоретичну формулу, що описує дрейф БСО в залежності від зміни досліджуваних параметрів моделі.

Приймемо як базові величини параметрів кроку інтегрування _{частоти коливань та амплітуду коливань 0.2 рад.}

1. Похибки бсо в залежності від кроку інтегрування

В цій серії визначалася величина дрейфу БСО за час 100 секунд при різних значеннях кроку інтегрування. Для цього були проведені моделювання, представлені на рис.3.1 – 3.5

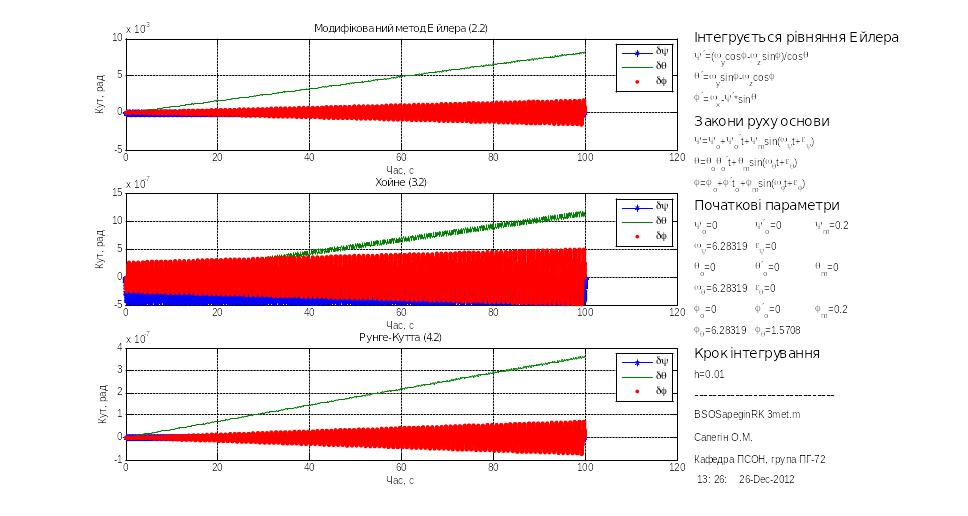
Рис.3.1 h=0.01

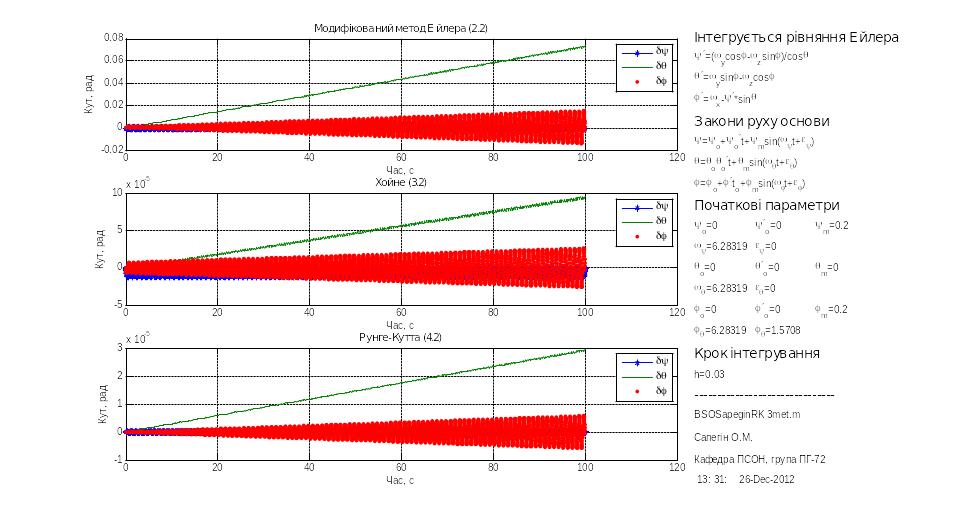
Рис.3.2h=0.03

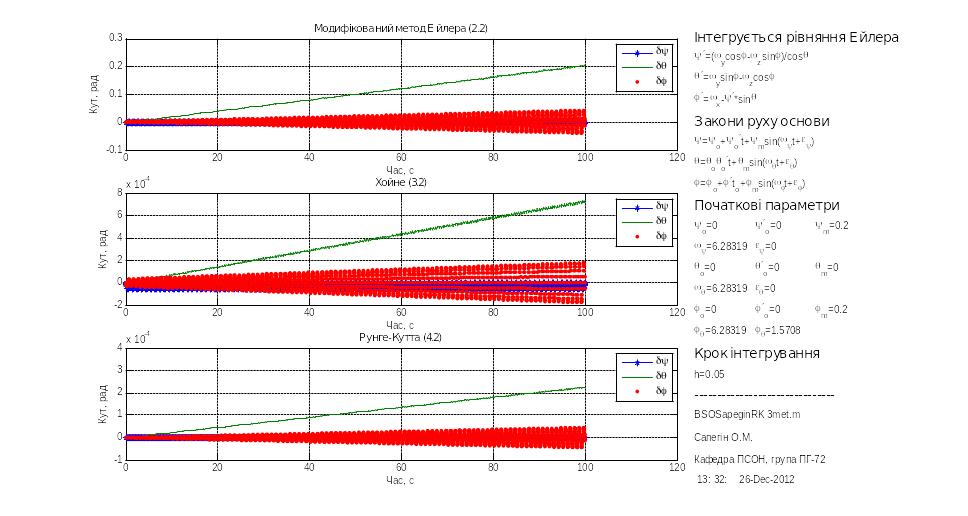
Рис.3.3h=0.05

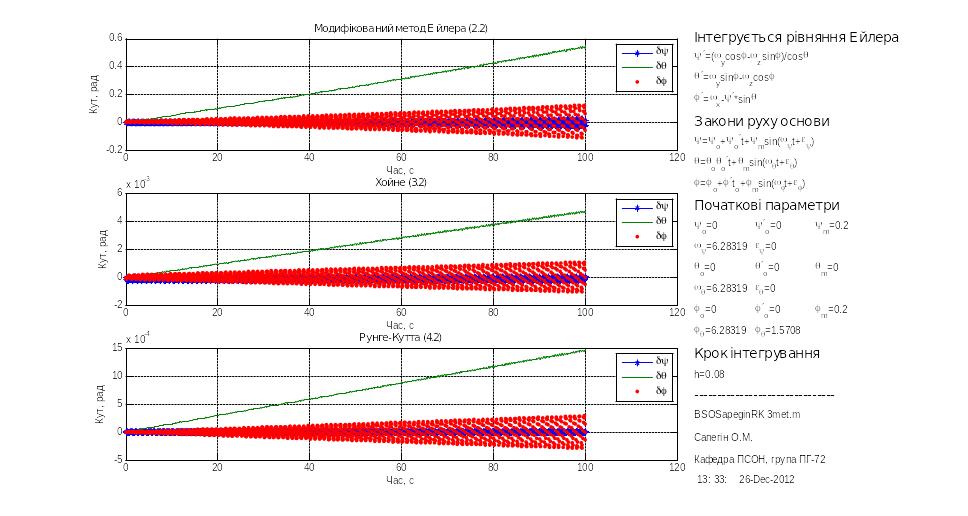
Рис.3.4h=0.08

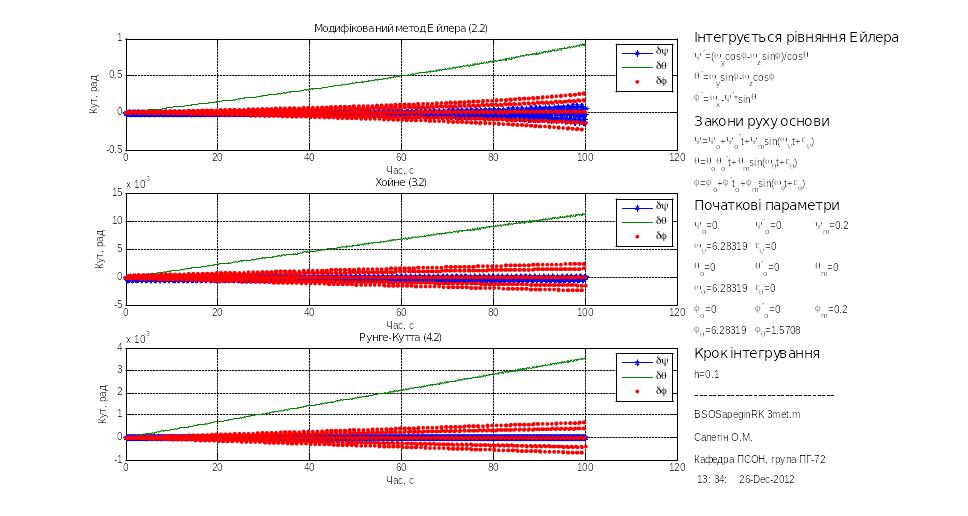
Рис.3.5h=0.1

В результаті були отримана залежність дрейфу БСО від кроку інтегрування що представлена на рис. 3.6.

Ці досліди проводилися з програмною моделлю побудованою з використанням кінематичних рівнянь Ейлера. Моделювання для рівнянь Пуассона та кватерніонних рівнянь руху проведено аналогічно. Результати представлені на рис. 3.7та 3.8.

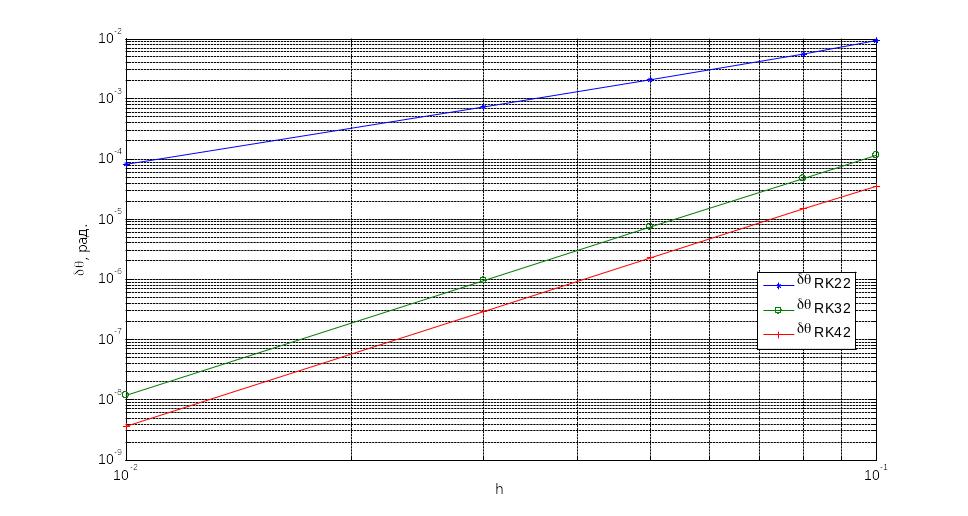
Рис.3.6 Кінематичне рівняння Ейлера

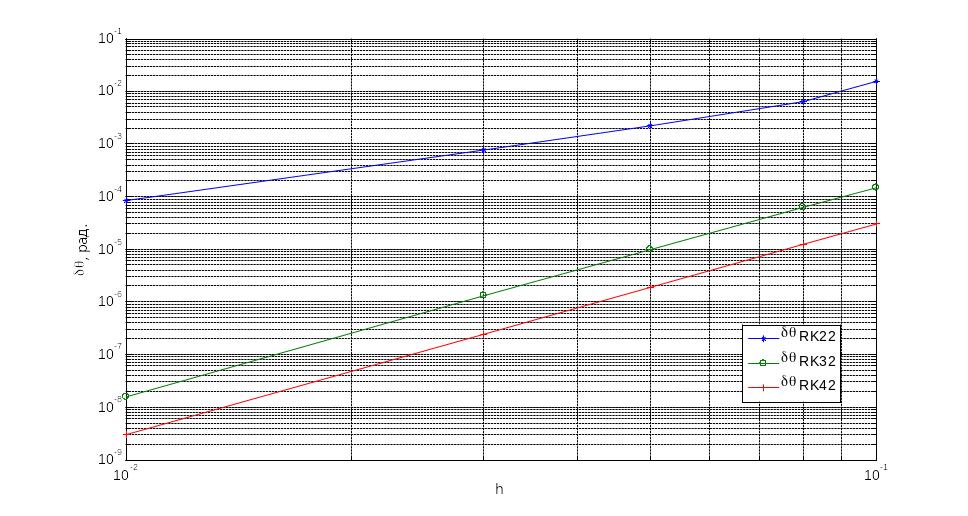
Рис.3.7 Кінематичне рівняння Пуассона

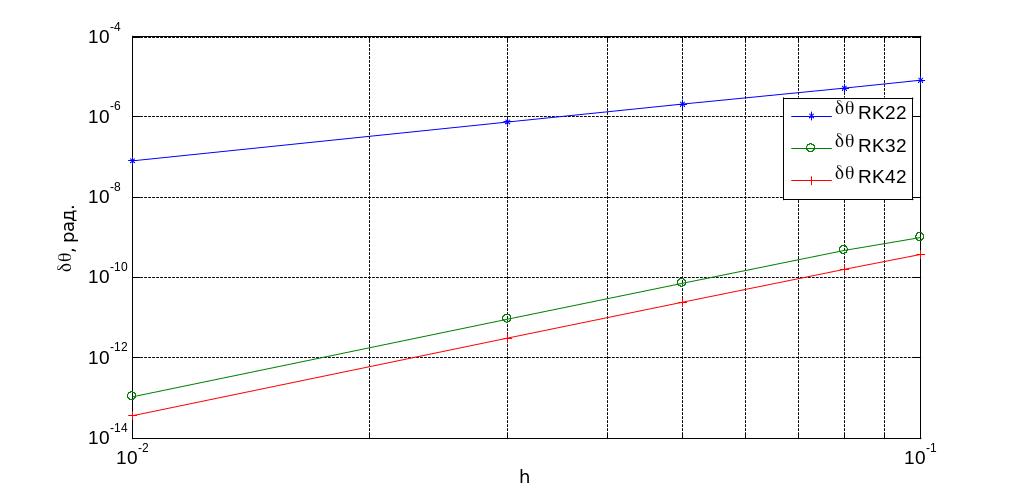
Рис.3.8 Рівняння у кватерніонах

2. Похибки бсо в залежності від частоти вимушених коливань

У минулій главі хід досліджень пояснювався на прикладі моделювання БСО заданої кінематичними рівняннями Ейлера. Аналогічні досліди були проведені і для встановлення залежності дрейфу БСО в залежності від частоти коливань основи, але у цій серії моделювань покажемо роботу програмної моделі що реалізує БСО описаної рівняннями Пуассона. Результати представлені на рис.3.9 – 3.12

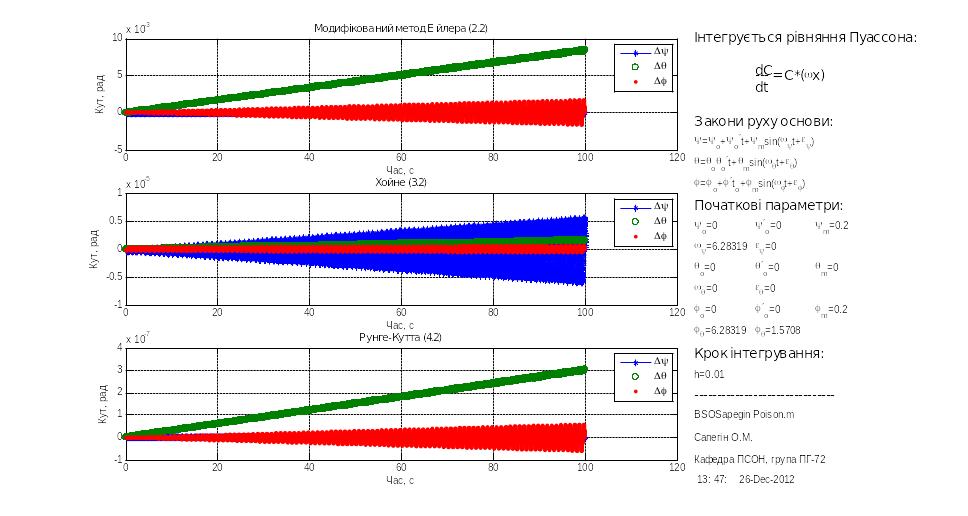
Рис.3.9

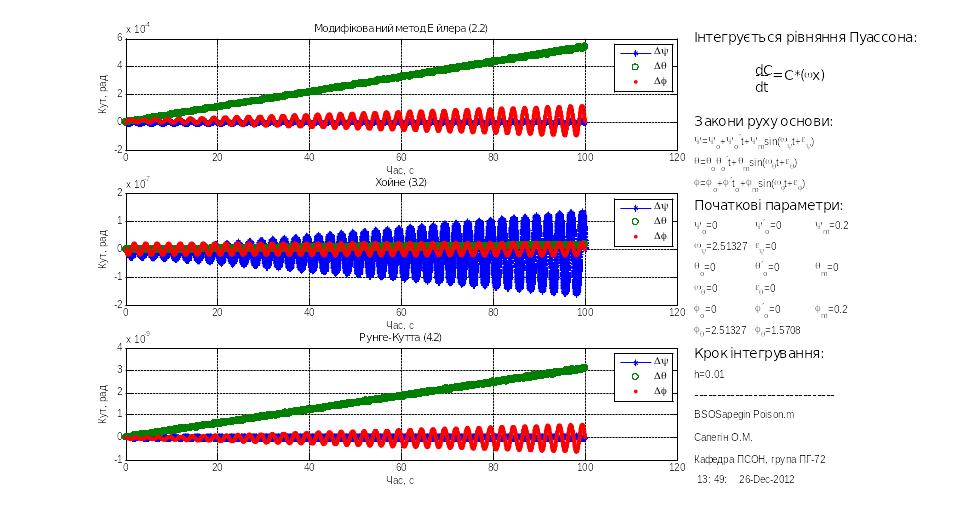
Рис.3.10

Рис.3.11

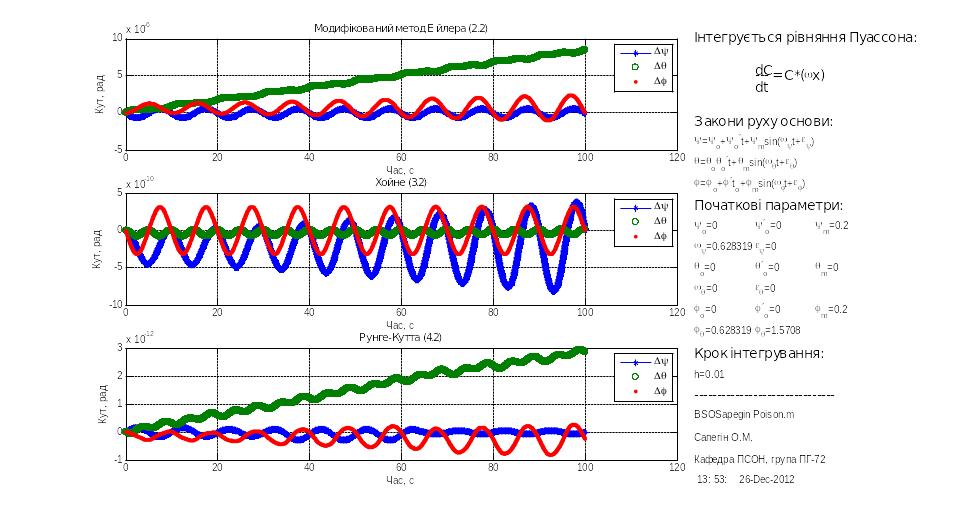
Рис.3.12

В результаті отримана залежність представлена на рис.3.13

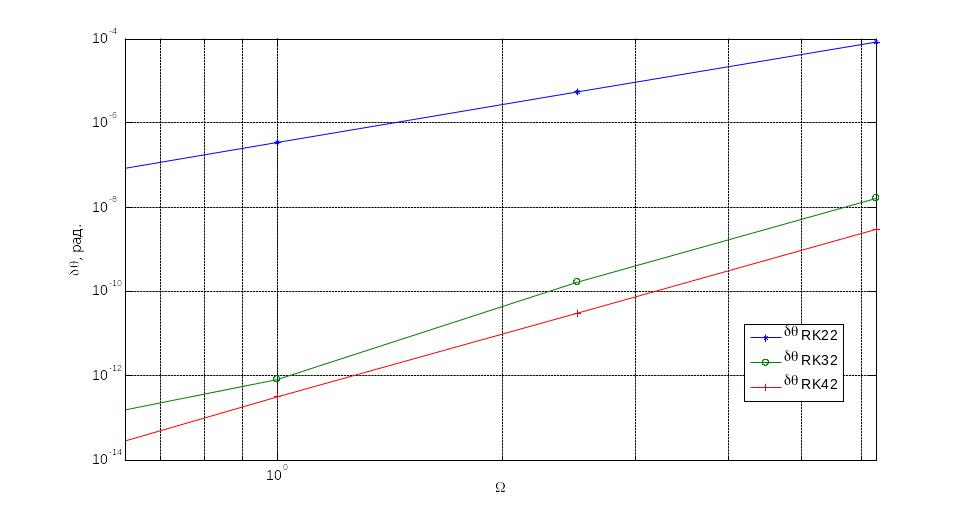
Рис.3.13 Кінематичне рівняння Пуассона

Моделювання для БСО заданих через кінематичні рівняння Ейлера та у кватерніонах проводилися аналогічно. Результати подано нижче на рис.3.14 та рис.3.15

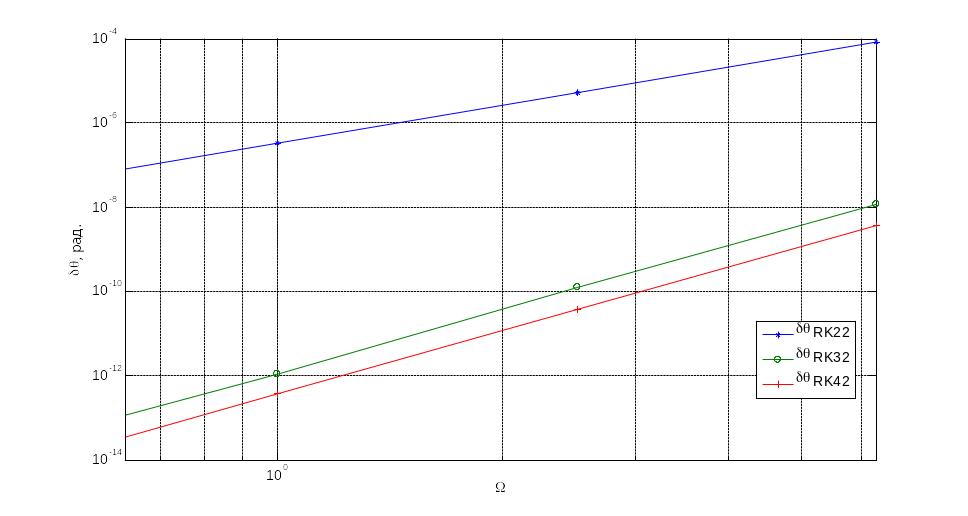
Рис.3.14 Кінематичне рівняння Ейлера

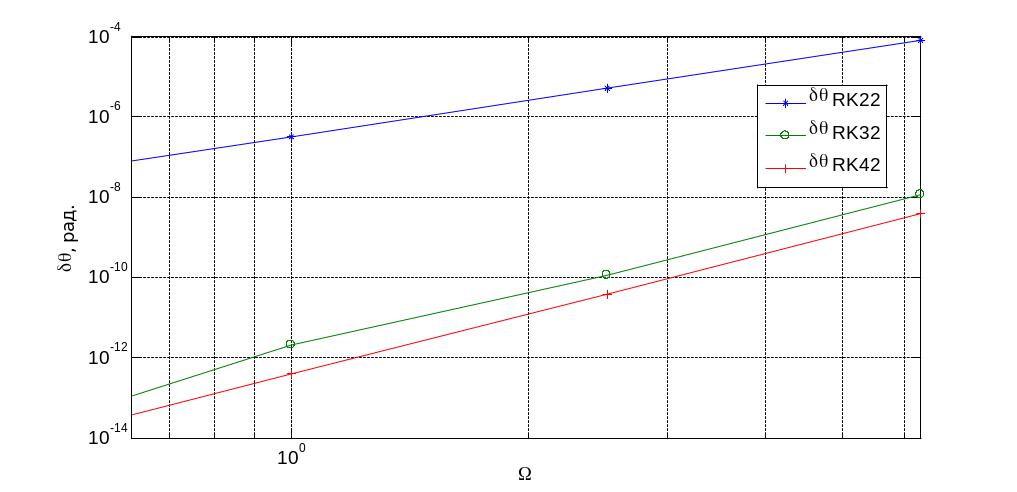
Рис.3.15 Кінематичне рівняння кватерніонах

3. Похибки бсо в залежності від амплітуди коливань

Покажемо хід моделювання на прикладі дослідження похибок БСО, побудованої у програмній моделі з використанням кватерніонних рівнянь.

Результати подано нижче на рис. 3.16 – 3.19.

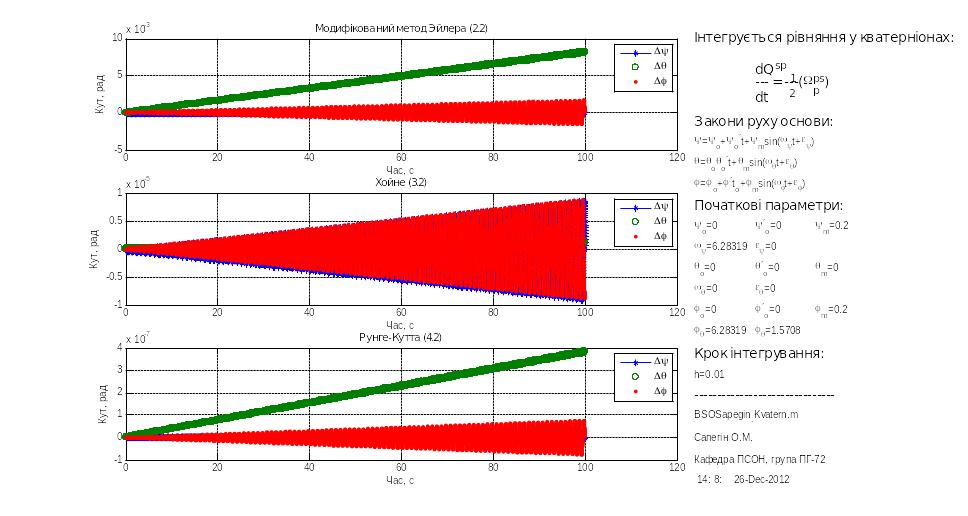
Рис.3.16 _рад., рад.

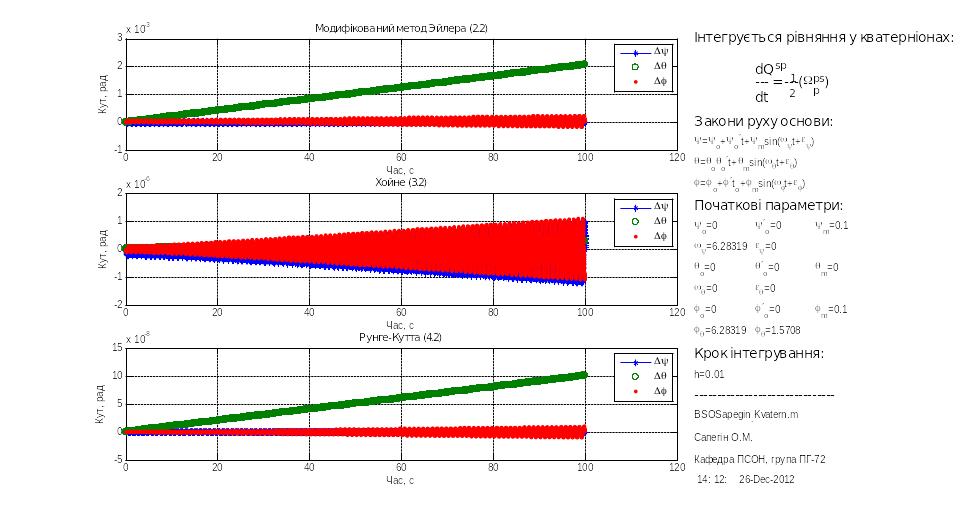
Рис.3.17 _рад., рад.

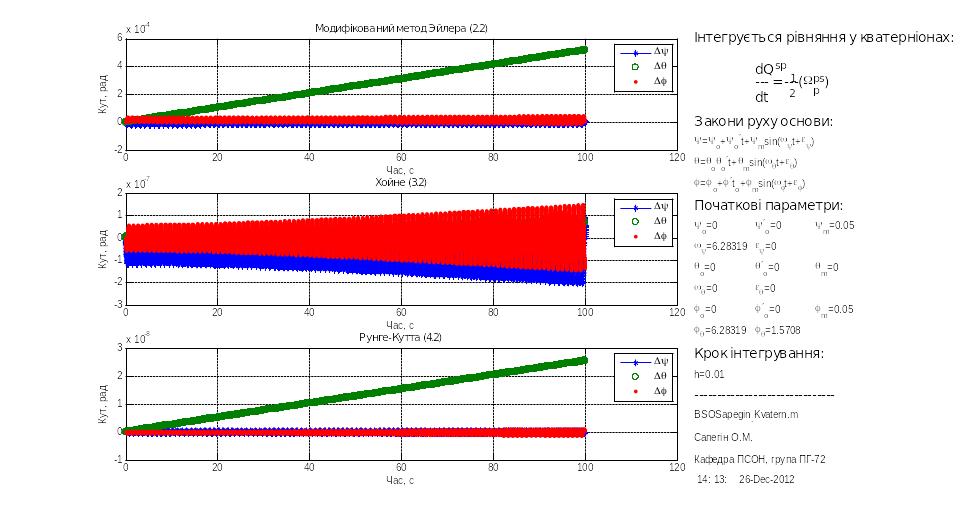
Рис.3.18 _рад., рад.

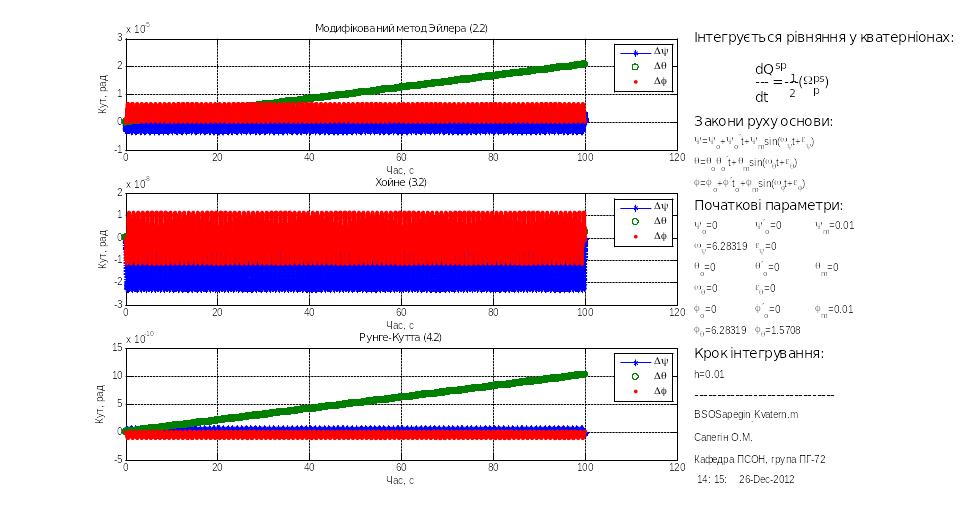
Рис.3.19 _рад., рад.

Залежність похибки БСО від амплітуди коливань основи подано на рис.3.20

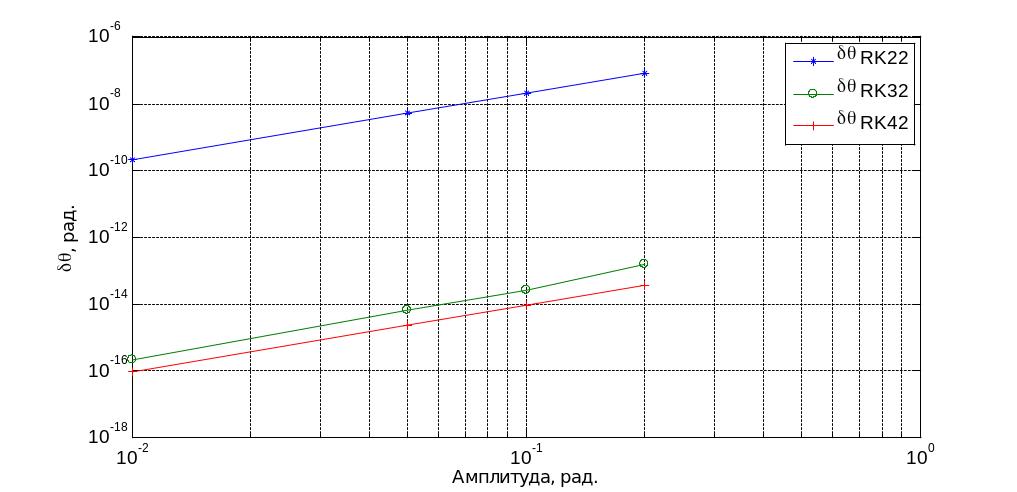
Рис.3.20 Кінематичне рівняння кватерніонах

Результати моделювань для БСО побудованих з використанням рівнянь Ейлера та Пуассона подано нижче на рис.3.21 та рис.3.22 відповідно.

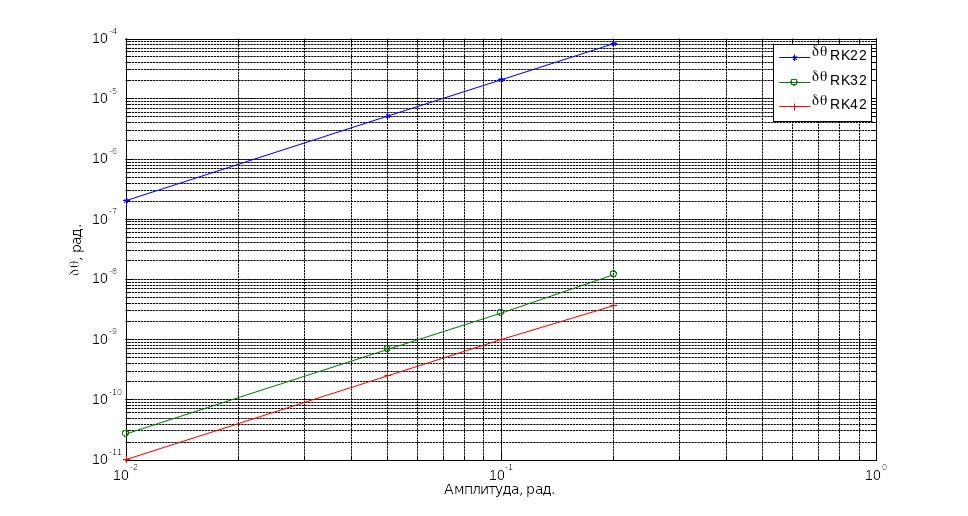
Рис.3.19 Кінематичне рівняння Ейлера

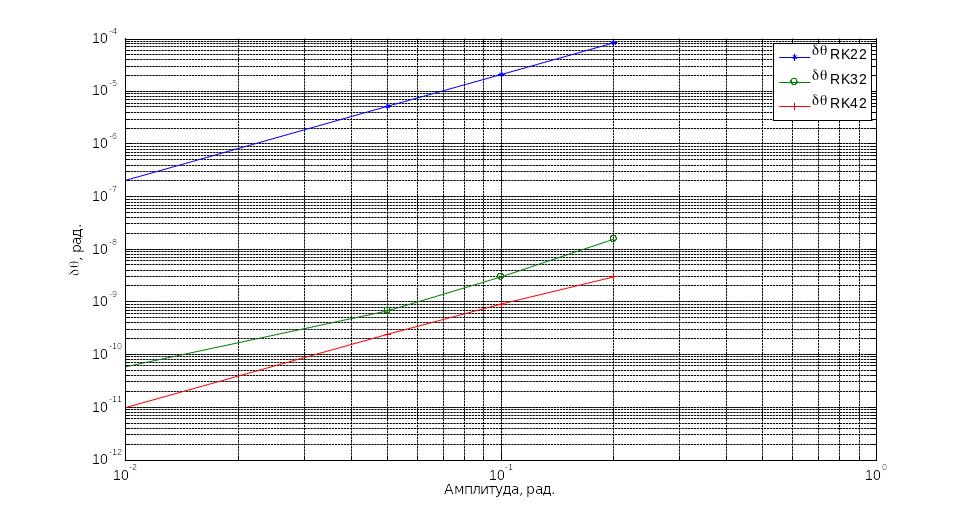
Рис.3.20 Кінематичне рівняння Пуассона

4. Виведення алгоритмічної формули дрейфу бсо

На основі даних отриманих у пунктах 3.1 – 3.3 виведемо загальну формулу дрейфу БСО.

У загальному вигляді вона має вигляд.

(3.1)

де , та а відповідно значення кроку, частоти та амплітуди;

p, nта m – показникистепеня;

K – сталий коефіцієнт.

Формула (3.1) описує дрейф приладу в тому випадку коли на нього впливає одразу три параметри: крок інтегрування, частота і амплітуда вібрації основи. Проте наші досліди проводилися при зміні лише одного з цих параметрів, тобто обидва інших були постійними. Тому для опису дрейфу БСО досліджуваного у пунктах 3.1 – 3.3 формула (3.1) перетвориться на

(3.2)

(3.3)

(3.4)

Показники степеня p, nта mможна визначити встановивши нахил логарифмічних характеристик представлених на рис.3.6 – 3.8, рис.3.13 – 3.15 та рис.3.20 – 3.21, представлених вище. Із них видно що p=2 для модифікованого метода Ейлера та p=4 для методів Хойне та Рунге-Кутта; n=2 для всіх методів інтегрування; m=2 також для всіх трьох методів.

Із (3.2) – (3.4) знайдемо коефіцієнти , та .

(3.5)

(3.6)

(3.7)

Підставимо раніше отримані значення дрейфів, параметрів та показників степеня до формул (3.5) – (3.7) то розрахуємо значення коефіцієнтів.

Знаючи коефіцієнти , та можемо знайти коефіцієнт K із формули (3.1).

_(3.8)

_{аналогічно} (3.9)

(3.10)

Із (3.8) – (3.10) знайдемо коефіцієнт Kпри чому значенняh, та а приймемо базові.

Як видно із розрахунків коефіцієнти Kмайже не відрізняються. Остаточна формула буде мати вигляд

(3.11)

Аналогічно отримано формули дрейфів для програмних моделей БСО побудованих на рівняннях Пуассона та у кватерніонах

Тоді остаточна формула дрейфу БСО побудованої на рівняннях Пуассона буде мати вигляд

(3.12)

Для БСО побудованої на кватерніонах:

Тоді остаточна формула дрейфу БСО побудованої на рівняннях у кватерніонах буде мати вигляд

(3.13)