44

ВСТУП

Серед різних навігаційних систем останнім часом широкий розвиток отримують інерціальні навігаційні систем (ІНС), які задовольняють цілому ряду таких важливих вимог, як автономність, перешкодостійкість, універсальність, необмежена область застосування, будь-який діапазон вимірювань навігаційних параметрів об'єкту. При цьому зберігається висока точність визначення місцеположення рухомого об'єкту. Завдяки цим перевагам ІНС знайшли широке застосування на підводних човнах, кораблях, наземних транспортних засобах, літаках, ракетах і космічних літальних апаратах.

У всіх ІНС опорні тригранники або фізично реалізуються гіростабілізованими платформами (ГСП), або вони жорстко пов'язані з об'єктом. Звідси витікає розділення ІНС на два великі класи: ІНС платформеного типу і безплатформені ІНС (БІНС).

Системи гідростабілізації (СГС), які використовуються в даний час на рухливих об’єктах відносяться до безплатформенних інерціальних навігаційних систем (БІНС) та безплатформенних інерціальних систем орієнтації (БІСО), так як їх перевагами є: малі габарити та їх вага, дешевизна датчиків, необмежені кути поворотів об’єкту відносно опорних базисів, а також мала енерговитрата.

Безплатформенні системи відносяться до інерціальних систем аналітичного типу без гіростабілізованої платформи (ГСП), їх чутливі елементи жорстко пов’язані з об’єктом.

Системи орієнтації, чутливі елементи яких (гіроскопи, кутові акселерометри й ін.) установлені на корпусі об’єкту, а їх положення щодо осей опорної системи координат обчислюється, називаються безплатформовими (БСО). Звичайно БСО входять до складу безплатформових інерційних навігаційних систем (БІНС) і забезпечують рішення задачі орієнтації, заміняючи собою інерційну курсовертикаль (ІКВ) або гіростабілізовану платформу (ГСП).

Однак, БІНС може скласти конкуренцію платформенним інерціальним системам тільки у випадку, якщо він матиме велику точність при збереженні надійності та дешевизни. Похибки БІНС по-перше залежать від похибок її основної підсистеми – безплатформенної інерціальної системи орієнтації (БИСО). Ці похибки в основному визначаться похибками трьох типів: гіроскопів, початкової виставки та обчислювальними, які обумовленні методичними похибками обчислювальних алгоритмів.

Однією з основних проблем недорогих датчиків (таких як ММГ) являється випадковий дрейф нуля. Існують різні методи боротьби з випадковою похибкою.

При проектуванні безплатформених інерційних навігаційних систем (БІНС) необхідно проводити обґрунтований вибір алгоритмів функціонування системи. Основним елементом алгоритмічного забезпечення БІНС є алгоритм чисельного інтегрування кінематичних рівнянь. Вибір цього алгоритму впливає на метрологічні характеристики безплатформеної інерційної навігаційної системи, і для його обґрунтування необхідно визначати похибку, виникаючу при інтегрування кінематичних рівнянь у самому алгоритмі.

1. Кінематичні рівняння орієнтації

На практиці орієнтацію у просторі твердого тіла часто визначають з використанням як вимірювачів трьох датчиків кутової швидкості (ДКШ), жорстко встановлених на цьому твердому тілі (корпусі об’єкту). ДКШ вимірюють поточні проекції абсолютної кутової швидкості тіла на три ортогональні осі системи координат, пов’язані з ним. Задача визначення поточної орієнтації тіла у просторі зводиться, у цьому випадку, до встановлення диференціальних рівнянь, інтегруючи які можна визначати поточні значення параметрів орієнтації. Ці рівняння називають кінематичними рівняннями орієнтації[2].

1.1 Рівняння орієнтації Ейлера

Найбільш поширеною формою кінематичних рівнянь є така, в якій вони подані через кути Ейлера послідовних поворотів.

Оскільки подання повороту через кути послідовних поворотів не є єдиним, форма кінематичних рівнянь у цьому випадку також не є єдиною і визначається цією послідовністю поворотів. З огляду на те, що кутове положення рухомого об’єкта зазвичай визначають послідовністю кутів Крилова, зображеною на рис. 1.1.

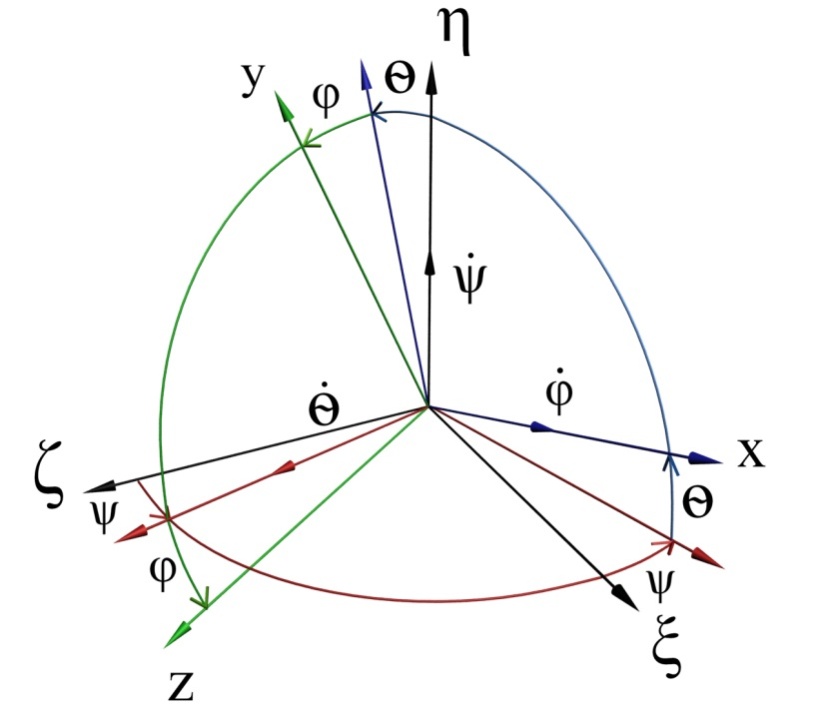
Рис 1.1 — Послідовність поворотів Крилова

При чому будемо вважати, що вектор кутової швидкості опорної системи координат відносно зв’язаної з об’єктом буде визначатися як

(1.1)

Спроектуємо кутову швидкість на вісі зв’язаної системи координат:

(1.2)

Визначимо із (1.3) похідні кутів поворотів :

(1.3)

Запишемо ці рівняння відносно похідних кутів:

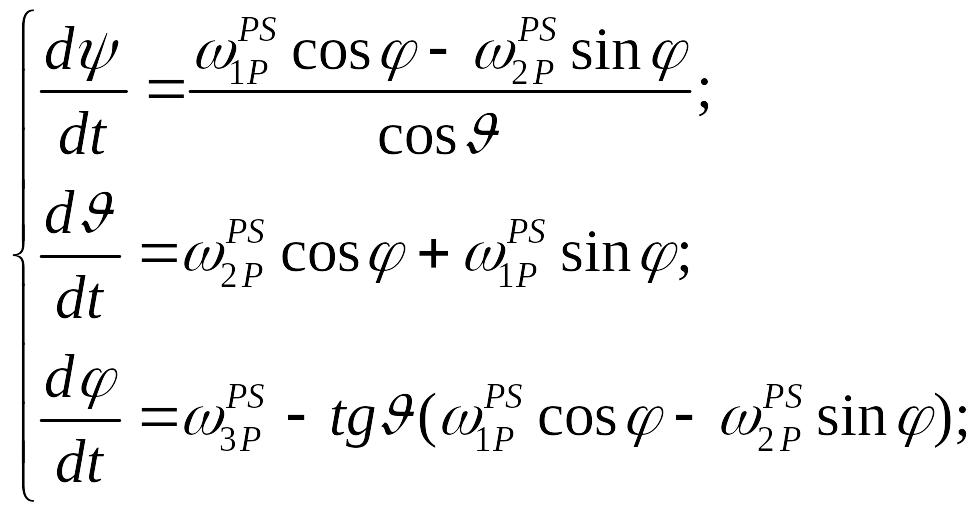(1.4)

Зазвичай ці співвідношення називають кінематичними рівняннями Ейлера.

1.2 Рівняння орієнтації Пуассона

Приймемо за основу кінематику поворотів зображену на рис.1.1

Матричне подання векторного співвідношення:

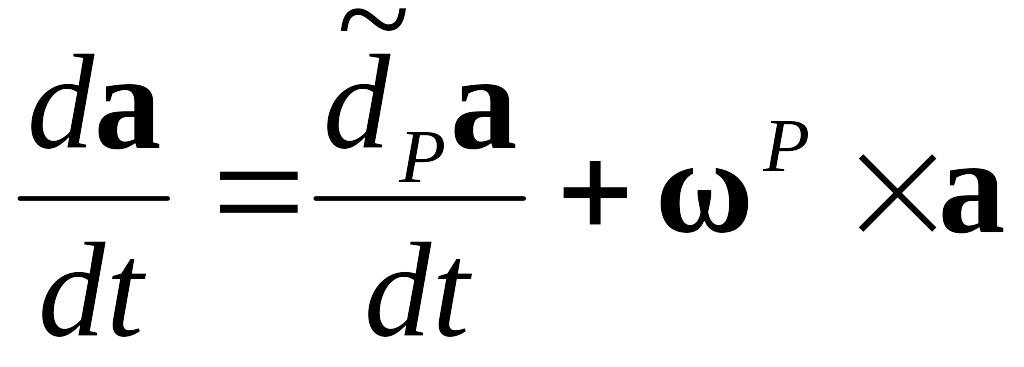_(1.5)

де - локальна похідна вектора (його швидкість відносно рухомої системи відліку), - вектор абсолютної кутової швидкості рухомої системи, матиме такий вид:

_(1.6)

де, і матриці-стовпці із проекцій вектора на осі відповідно нерухомої й рухомої системи відліку, - матриця напрямних косинусів переходу від нерухомої до рухомої системи відліку,

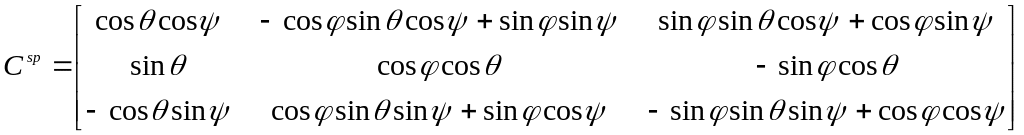_(1.7)

- позначення кососиметричної матриці із проекцій вектора кутової швидкості системи Р відносно системи S на її осі:

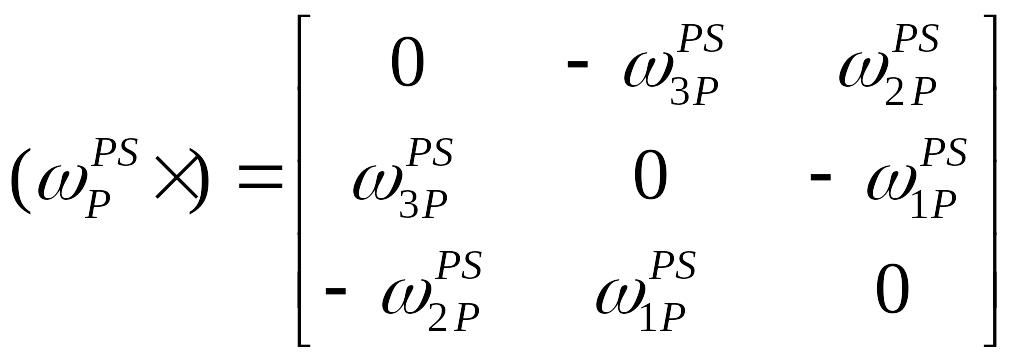_(1.8)

_{Зіставляючи 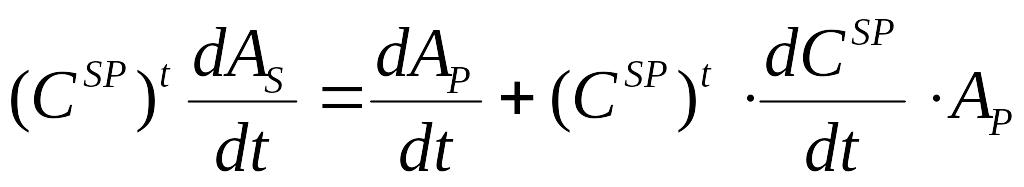із (1.6), можна зробити висновок, що:}

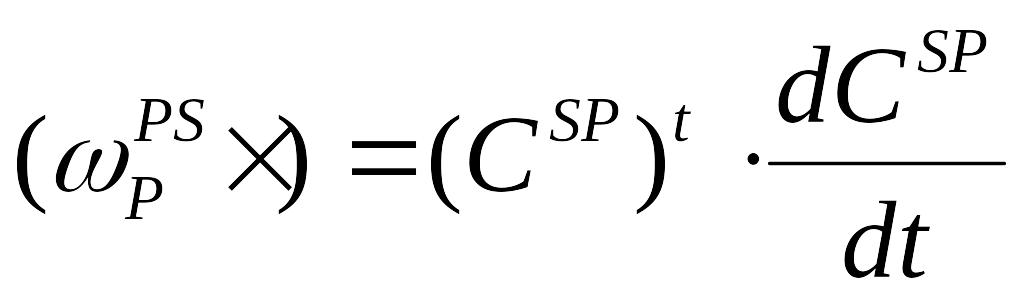_(1.9)

_{Це співвідношення зв'язує проекції кутової швидкості обертання системи Р відносно S на осі системи Р з матрицею напрямних косинусів між цими системами відліку. В дещо зміненій формі}

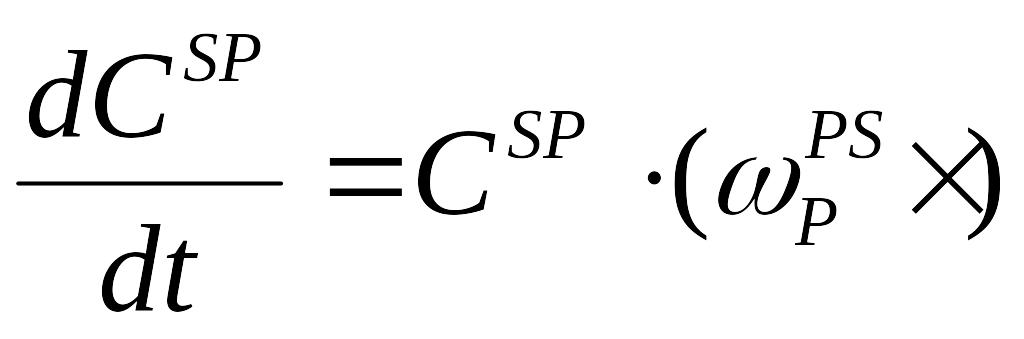_(1.10)

_{це ж співвідношення може прислужиться задля визначення похідної від МНК за заданими проекціями кутової швидкості. Воно називається рівнянням Пуассона.}

_{Якщо матричне подання (1.5) записати через проекції на осі абсолютної системи}

_(1.11)

_де,

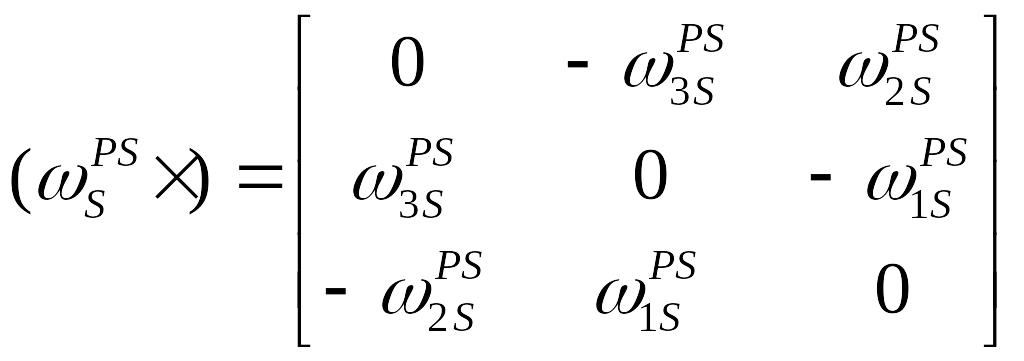_(1.12)

_{то, порівнюючи (1.6) з 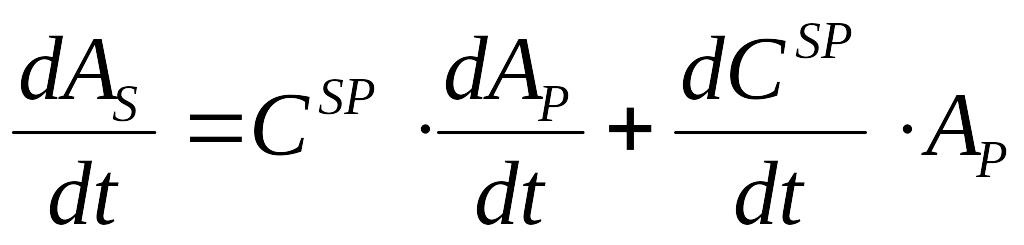, можна одержати аналогічну залежність для проекцій кутової швидкості на нерухомі осі}

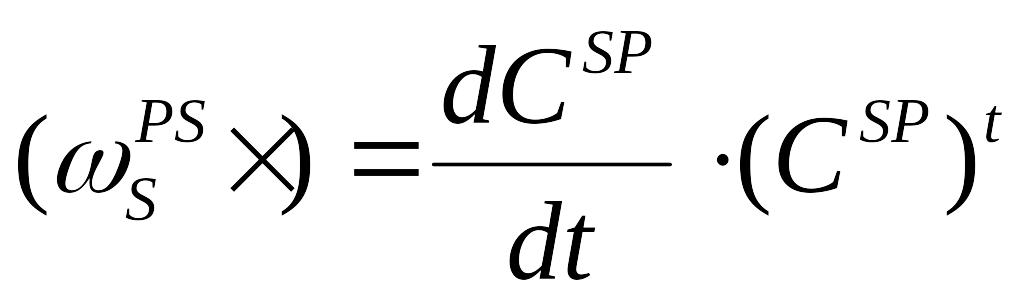_(1.13)

_звідки

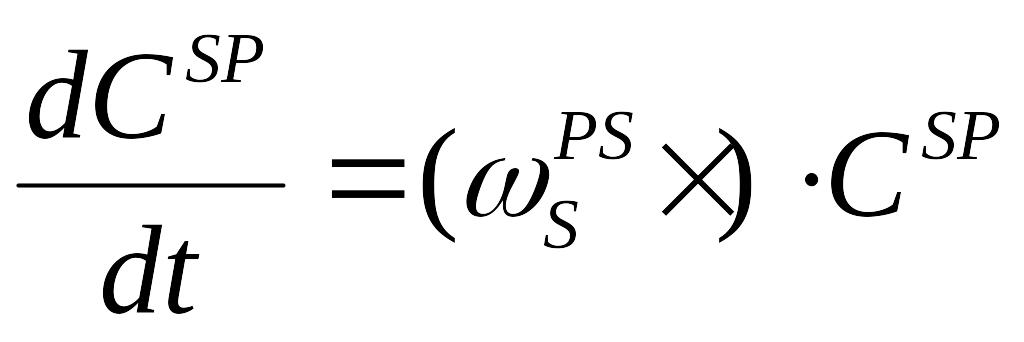_(1.13)

_{яке є однією з форм того ж рівняння Пуассона.}

1.3 Рівняння орієнтації у кватерніонах

Хоча кінематичні рівняння руху Ейлера і Пуассона досить просто отримати для заданої кінематики руху, проте їх використання часто не вигідно через надмірну складність математичних моделей і ймовірність їх виродження при деяких параметрах орієнтації об’єкта.

Ці проблеми можна частково вирішити перейшовши до іншого способу опису кінематики рухомого об’єкта у просторі – використання кватерніонів поворотів.

Кватерніоном називають гіперкомплексне число із трьома уявними одиницями. У загальному випадку воно має вигляд

_,

_де – деякі дійсні числа, а – уявні одиниці.

Алгебра кватерніонів дозволяє подати поворот у просторі у простій і зручній формі. Таке подання базується на наступній фундаментальній теоремі:

Якщо і є не скалярними кватерніонами, то величина

(1.14)

є кватерніоном, норма і скалярна частина якого збігається з нормою і скалярною частиною кватерніону , а векторна частина виходить повертанням векторної частини кватерніону по конусу навколо осі напрямку кватерніону на подвійний кут кватерніону .

Операція (1.14) змінює лише векторну частину кватерніону, тому її можна розглядати як операцію перетворення вектора у вектор згідно формули

(1.15)

Це перетворення є обертанням навколо деякої осі, причому перетворення у вигляді (1.15) одразу визначає вісь цього обертання. Цією віссю є векторна частина кватерніону , оскільки ця вісь не змінюється цим перетворенням:

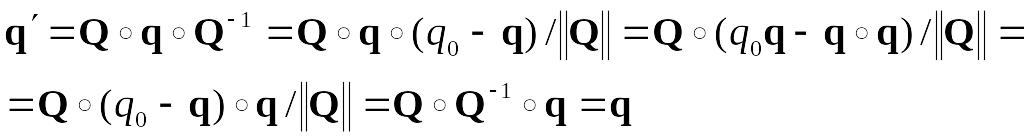(1.16)

Щоб подати поворот системи відліку навколо деякої осі на кут , досить у перетворенні (1.15) узяти як перетворюючій кватерніон нормований кватерніон із кутом кватерніону, що дорівнює половині кута :

(1.17)

де – є одиничним вектором напрямку, навколо якого здійснюється поворот на кут . Наприклад, для опису повороту від початкової системи відліку S можна під розуміти вектор-кватерніон вигляду:

; (1.18)

де, – напрямні косинуси осі повороти у початковій системі відліку.

Чотири компоненти кватерніону повороту (1.17):

(1.19)

одержали назву параметрів Ейлера або параметрів Родріга-Гамільтона.

Перейдемо до подання поворотів систем відліку. Потрібно описати поворот від системи S до системи Р. Тоді, позначаючи кватерніон такого повороту через

(1.20)

де – одиничний вектор осі, поворот навколо якої системи відліку S на кут переводить її у систему P, можна подати у цілому перетворення будь-якого вектора-кватерніона , заданого своїми проекціями на осі системи Р, у вектор-кватерніон , що складається із проекцій цього вектора на осі початкової системи, у такому вигляді

(1.21)

Через те що кватерніон повороту має однакові складові як у початковій, так й у кінцевій системі відліку, перетворення може бути записане у двох еквівалентних формах

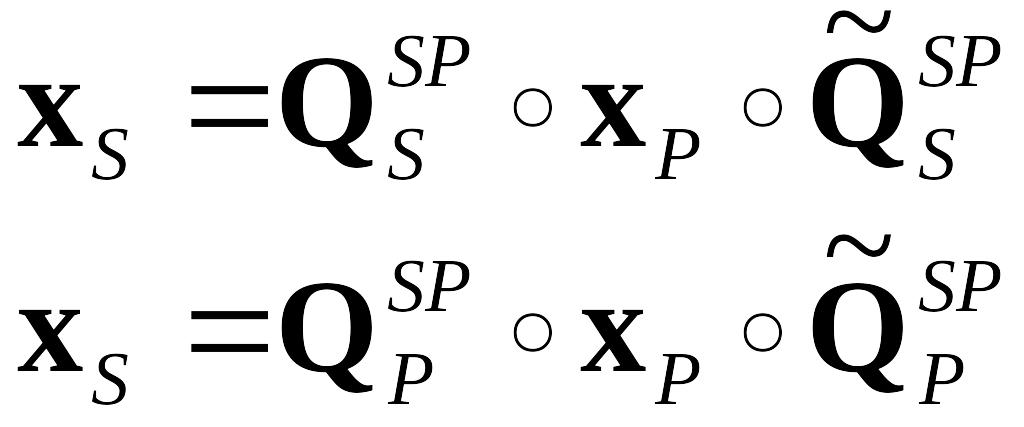(1.22)

Зворотний перехід - від системи Р до системи S - може бути описаний кватерніоном , який, очевидно, матиме той самий напрямок векторної частини, що й кватерніон , той самий аргумент, але протилежного знаку,

тобто буде спряженим до останнього:

(1.23)

Відшукаємо явні вирази компонент кватерніону

(1.24)

У початковому стані система відліку Р збігається із системою S. В ній задано вектор своїми проекціями на осі системи Р (отже, і S):

_(1.25)

Потім здійснюється поворот системи Р у нове положення. Цей поворот описаний кватерніоном , векторна частина якого задана своїми проекціями на осі тієї ж системи S:

_(1.26)

Разом із системою Р повертається і вектор . Потрібно визначити проекції цього вектора на осі системи S.

Враховуючи в (1.23) вирази (1.24)…(1.26) і здійснюючи операції кватерніонного множення, одержимо:

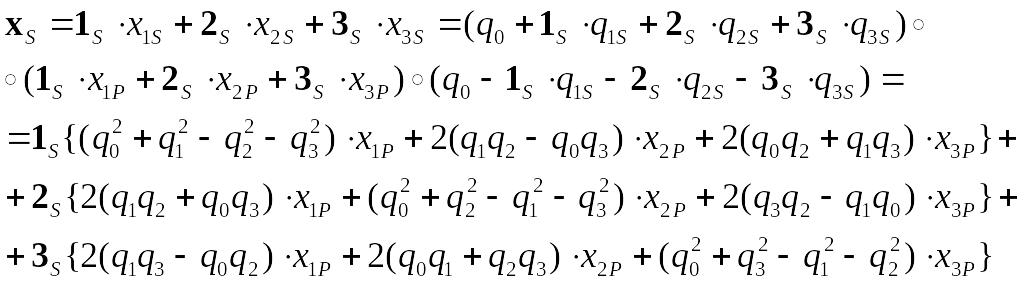
З цього випливає

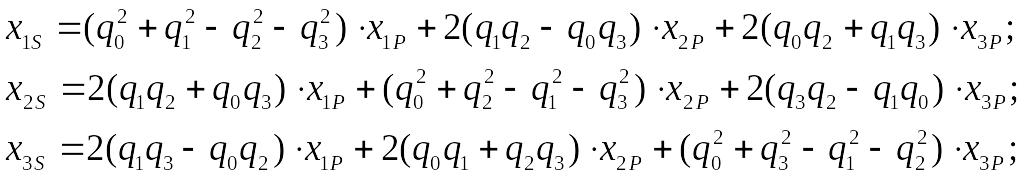
Матриця напрямних косинусів визначається параметрами кватерніону повороту у такий спосіб:

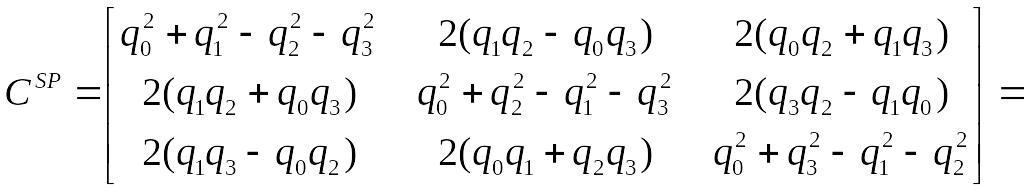
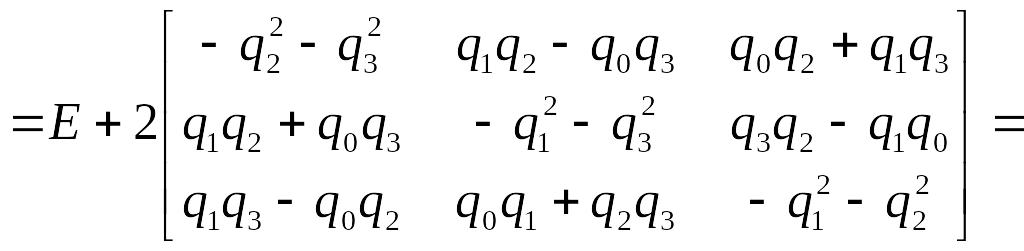
_(1.27)

_{Тут використане позначення}

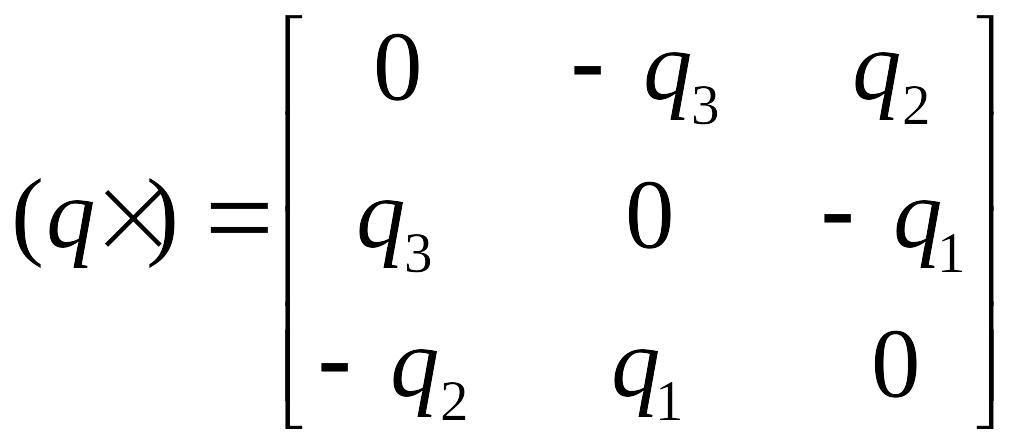_(1.28)

яке є кососиметричною матрицею, яка складається з компонентів векторної частини кватерніону на кшталт того, як кососиметрична матриця складається із проекцій вектора.

_{З (1.27) легко визначити слід МНК:}

(1.29)

що доказує співвідношення (1.17).

Неважко довести, що (1.27) є кватерніонним аналогом співвідношення (1.18). Дійсно, враховуючи, що у цьому випадку скалярна частина кватерніону переходу від початкової системи S до кінцевої P дорівнює , а компоненти векторної частини кватерніону повороту зв‘язані із проекціями одиничного вектора співвідношеннями

; ; ;

можна перетворити (1.24) наступним чином:

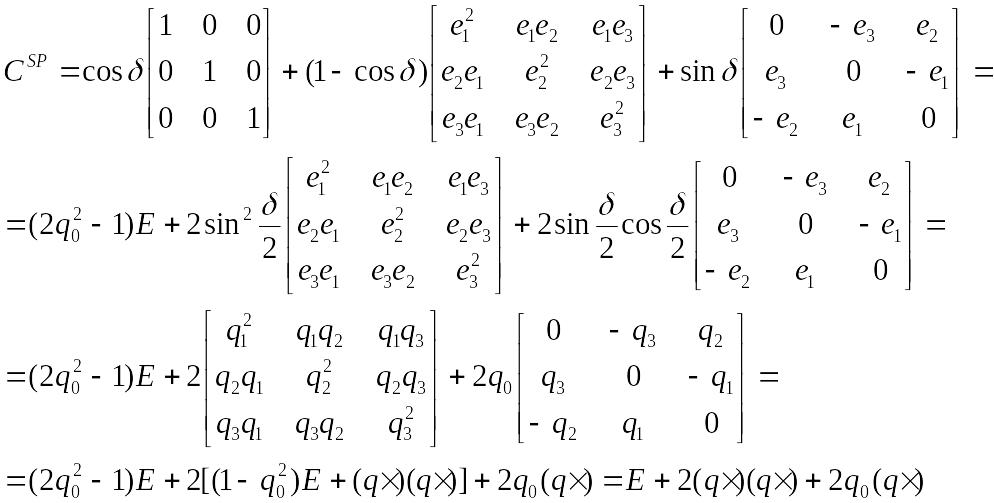
_{Установимо тепер правило перетворення кватерніонів поворотів при складанні поворотів. Нехай перший перехід від початкової системи відліку S до проміжної системи Т описується кватерніоном , а другий перехід - від системи Т до системи Р описується кватерніоном Тоді, користуючись (1.21), можна записати}

Підставивши другий вираз у перший, матимемо

_{порівнюючи який із третім виразом, одержимо}

_(1.30)

Отримаємо кінематичні рівняння руху у кватерніонах

, ,

у другій формі (через кватерніон повороту в рухо­мій системі координат)

_.

Візьмемо похідну за часом з обох частин цього рівняння. Матимемо

(1.31)

Перепроеціюємо одержаний результат на осі системи Р:

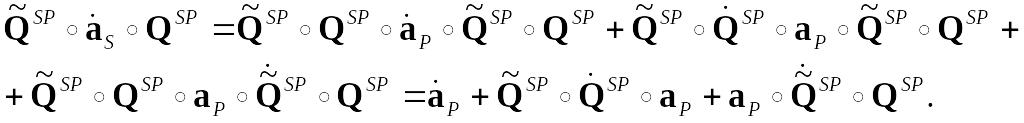
Використаємо співвідношення

яке випливає з того, що кватерніон повороту є нормованим. Продиференціюємо його за часом:

.

З урахуванням цього можна записати (крапка зверху позначає похідну за часом):

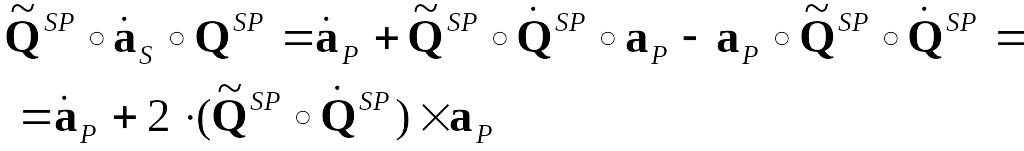_(1.32)

Тут враховано властивість:

, і позначено векторний добу­ток векторної частини кватерніона на наступний вектор.

Тепер порівняємо співвідношення (1.31) і . Вони, очевидно, опису­ють одну й ту саму залежність дещо відмінними засобами. Є повна відповід­ність один одному кожного із членів цих двох рівнянь. Тому, зіставляючи останні члени рівнянь, можна зробити висновок, що векторний кватерніон має дорівнювати вектор-кватерніону із проекцій на осі системи Р вектора кутової швидкості обертання системи Р відносно системи S. Позначаючи цей кватерніон

_(1.33)

можна встановити таке кватерніонне кінематичне рівняння:

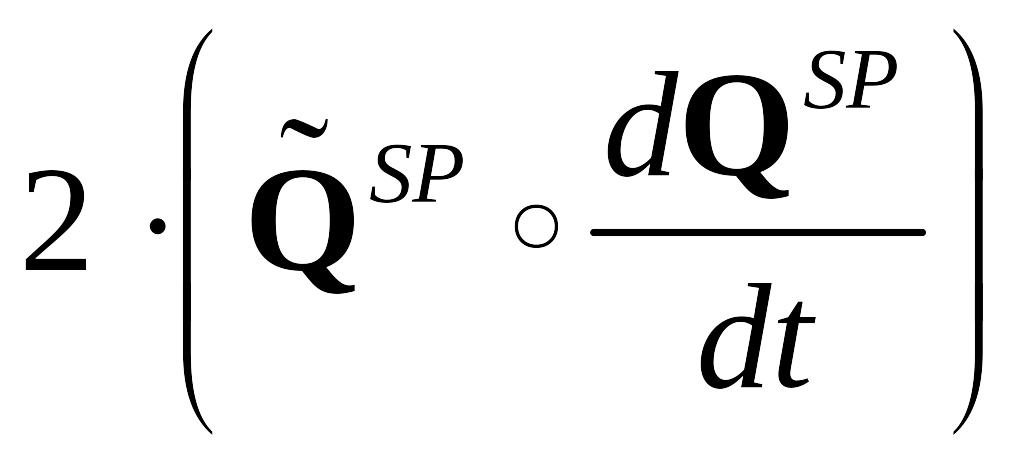. (1.34)

Резюмуючи, можна сформулювати таке правило визначення вектора кутової швидкості:вектор-кватерніон із проекцій кутової швидкості рухо­мої системи відліку відносно нерухомої на осі рухомої системи дорівнює по­двійному добутку спряженого кватерніона повороту нерухомої системи до рухомої на похідну за часом кватерніона того ж повороту.

Розв’язуючи рівняння (1.34) відносно похідної, отримаємо:

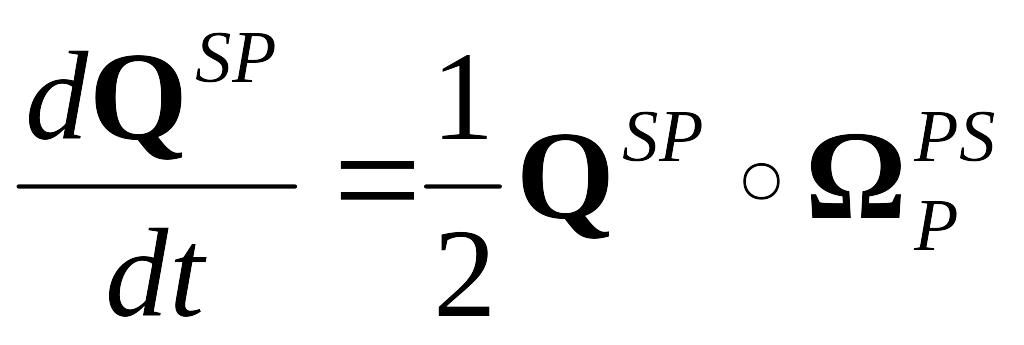
Це й є кінематичне рівняння у кватерніонах, яке визначає швидкість змінювання компонентів кватерніона повороту тіла через його кутову швидкість.

Для використання кватерніонного кінематичного рівняння орієнтації

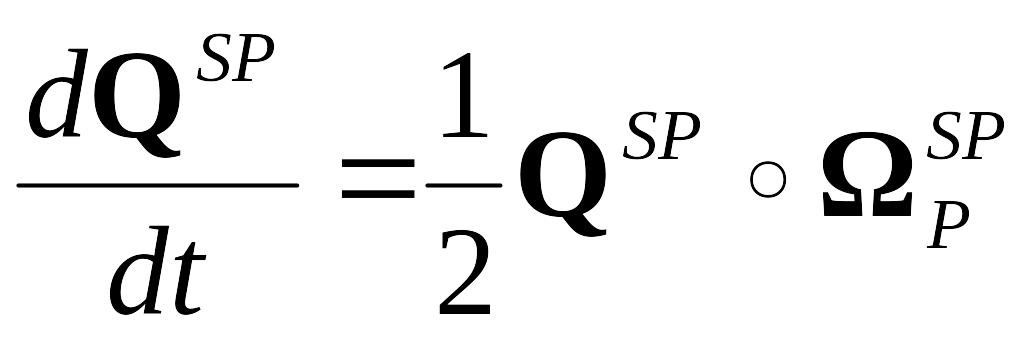(1.35)

У теоретичних дослідженнях і розрахунках на ЕОМ зручніше використовувати його матричну форму, яка ґрунтується на поданні кватерніона через його скалярну частину і матрицю-стовпець зі складових його векторної частини . При цьому слід зважити на те, що кватерніон кутової швидкості є вектором-кватерніоном, тобто його скалярна частина дорівнює нулю. Тоді рівняння (1.35) можна звести до таких двох матричних:

; (1.36)

, (1.37)

Де – матриця стовпець з виміряних проекцій кутової швидкості, ; – кососиметрична матриця, що відповідає матриці-стовпцю