17. Свойства дисперсии
1)D(C)=0, док-во: подставить С в опред. D.
2)D(kX)=k^2D(X), док-во: аналогич.
3)D(X)=M(X^2)-[M(X)]^2, док-во: раскрыть скобки в опред-и D. 4)D(X+Y)=D(X-Y)=D(X)+D(Y).
18. Биномиальное распределение
Дискретная СВX имеет биномиальный з-н с параметрами n и р, если она принимает значения 0, 1, 2,..., m,..., n с вероятностями P(X=m)=Cnmpmqn-m, где 0<p<1, q=1-p. Вероятность вычисляется по формуле Бернулли. M(x)=np, Д(x)=npq. n-независимые испытания, Pn(k)= CnKpkqn-k, то это ряд распределения. M(xk)=0*q+1*p=p, X=x1+x2+…+xn, M(∑xi)=∑ M(xi), M9x)=np., Д(xk)= ∑ (xi-mx)pi, Д(x)=∑ Д(xk)=npq
19. Распределение Пуассона
ДСВ Х, принимающая целочисленные значения от 0 до ∞, распределена по закону Пуассона с параметром а, если справедливо утверждение: Pа(k)=аk/k! * e-а. СВ- значения находятся в биномиальном законе. а=np, a=λt, где λ-интенсивность. М(х)=Д(х)=а. p-маленькое, р≤1, n-большое, m-небольшое. np=npq.
Дискретная СВX имеет:этот з-н с параметром λ > 0, если она принимает значения 0, 1, 2,..., m (бесконечное, но счетное множ-во значений) с вер-стямиP(X=m)=λme-λ \m! . (n→∞, p→0).
20. Геометрическое распределение
p-поражение, q-не поражение. СВ принимает значения 1,2,3… Pn(k)=qk-1*p
M(x)=1/p, Д(x)=q/p2
Дискретная СВХ=m имеет геометрическое р-е с параметром р, если она принимает значения 1,2,..., m... (бесконечное, но счетное множ-во значений) с вер-стямиP(X=m)=pqm-1, где 0<p<1, q=1-p. Теорема.(без док-ва) Если СВ . Х распределена по геометрич. р-ю, то М(Х)=1\р, D(X)=q\p^2.
21. Равномерное распределение
СВХ имеет этот з-н р-я на отрезке [a,b], если ее плотность вер-сти постоянна на этом отрезке и =0 вне его, т.е.
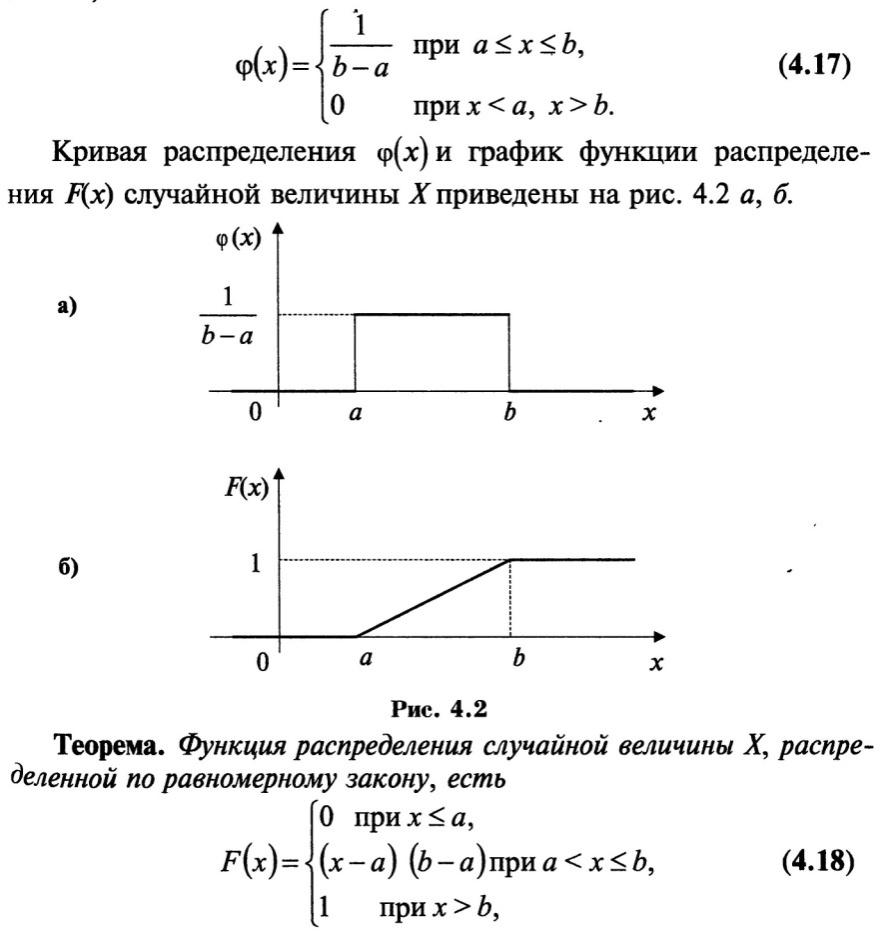
22. Нормальное распределение. Распределение Гаусса
Параметры
а, σ^2
e,
σ – некоторые параметры. М(Х)=а, D(X)=σ^2.
P(aльфа≤x≤b)= Ф((b-a)/σ)-Ф((альфа- а)/σ) –формула Лапласа для нормального закона. P(aльфа≤x≤b)= F(b) -F(альфа).
23.Экспонентациальное распределение(показательное)
Параметр
р-я λ>0.
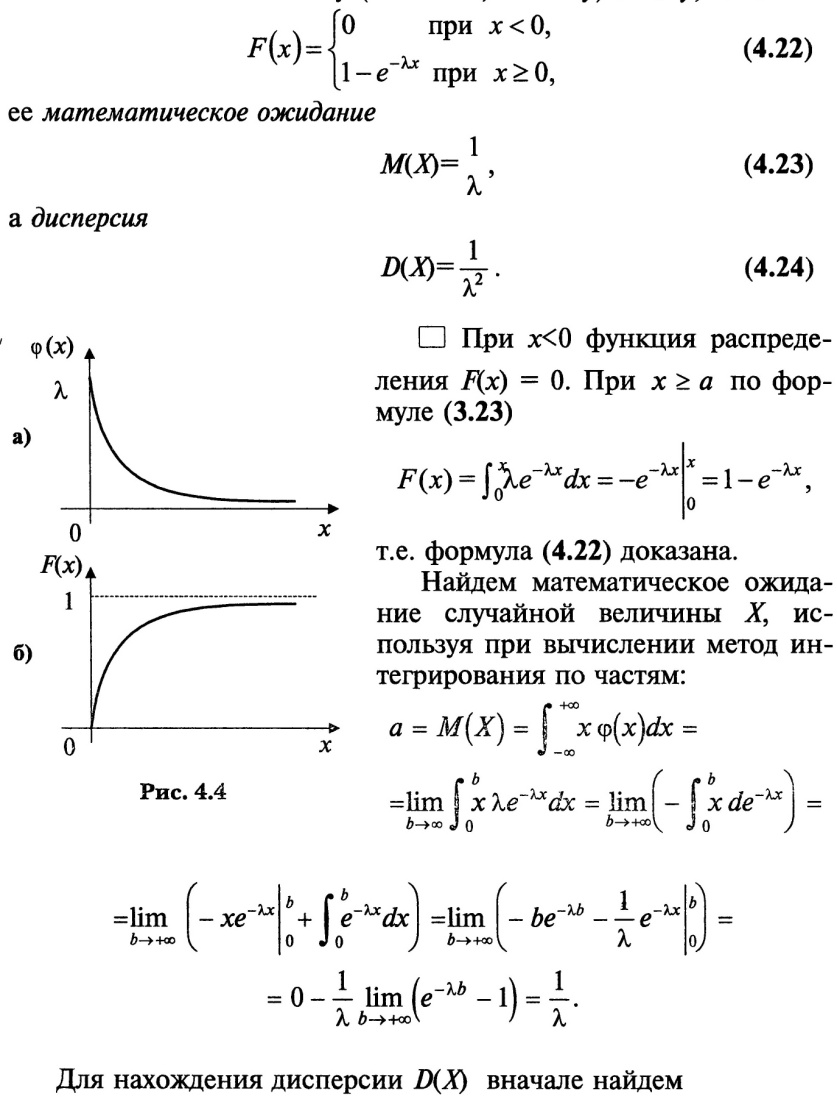
24.Системы СВ. Функция распределения двумерной СВ, св-ва
Система СВ- совокупность n-СВ, рассматриваемых одновременно. (n-СВ)/Ω. Закон ДСВ- любое правило, позволяющее перечислить все возможные значения появления пар и указать вероятности их появления.
Ф-я распред-я п-мерной случ. величины (Х1,Х2,...Хn) - ф-я F(xl,x2,...,xn), выражающая вер-сть совместного выполнения n неравенств X1<x1, X2<x2…Xn<xn, т.е. F(x1,x2…xn)=P(X1<x1, X2<x2…Xn<xn). Для двумерной: F(x,y)=P(X<x, Y<y). Свойства F(x,y): 1) 0≤ F(x,y)≤1. Утверждение следует из того, что F(x,y) есть вер-сть. 2) F(x,y) – неубывающая по каждому аргументу, т.е. при x2>x1 F(x2,y)≥ F(x1,y); при y2>y1 F(x,y2)≥ F(x,y1). 3) Если хотя бы один из аргументов обращается в -∞, F(x,y)= 0, т.е. F(x, -∞)=F(-∞,y)=F(-∞,-∞). 4) Если один из аргументов обращается в +∞: F(x, +∞)=F1(х), F(+∞, у)=F2(у), где F1(x) и F2(y) – ф-и р-я случ. величин Хи Y. 5) F(+∞,+∞)=1.
Геометрически ф-я распр-я есть некоторая поверхность, обладающая указаннымисв-вами.