40. Вариационный ряд. Полигон частот

Вариационный ряд - ранжированный в порядке возрастания (или убывания) ряд вариантов с соответствующими им частотами или частостями. Вариационный ряд наз-тсядискретным, если любые его варианты отлич-ся на постоянную величину, и - непрерывным (интервальным), если варианты могут отличаться один от другого на сколь угодно малую величину. Задается в виде табл со знач Х, частотами и частостями. Графическ изображение: 1)Полигон - для изображения дискретного ряда и представляет собой ломаную, зависимость накопленных частот от Х.

41. Построение интервального вариационного ряда. Гистограмма

Если промежуток между наименьшим и наибольшим значениями признака в выборке разбить на несколько интервалов одинаковой длины, каждому интервалу поставить в соответствие число выборочных значений признака, попавших в этот интервал, то получим интервальный вариационный ряд. Если признак может принимать любые значения из некоторого промежутка, то есть является непрерывной случайной величиной, приходится выборку представлять именно таким рядом. Если в вариационном интервальном ряду каждый интервал [=i; =i+1) заменить лежащим в его середине числом (=i+=i+1)/2, то получим дискретный вариационный ряд.Такая замена вполне естественна, так как, например, при измерении размера детали с точностью до одного миллиметра всем размерам из промежутка [49,5; 50,5), будет соответствовать одно число, равное 50. Гистограмма – для интервального ряда, зависимость частоты от Х.

42.Эмперическая функция распределения, ее свойства

Эмпирическая функция р-яFn(x) - относительная частота (частость) того, что Х примет значение, меньшее заданного х, т.е. Fn(x)=w(X<x)=w (накопленная). Для данного х w=n(нак)\n. Среднее арифметическое , где xi - варианты дискретного ряда или середины интервалов; ni - соответствующие им частоты; wi=ni\n - частость. Св-ва средней: 1)Средняя постоянной = самой постоянной. 2)Если все варианты увеличить (уменьшить) в одно и то же число раз, то средняя увеличится (уменьшится) во столько же раз . 3)Если все варианты увеличить (уменьшить) на одно и то же число, то средняя увеличится (уменьшится) на то же число: 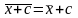. 4)Средняя отклонений вариантов от средней: 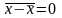. 5) . 6)Общая средняя, если ряд состоит из нескольких групп: , где xi групповая средняя i-ой группы.Суммируется по кол-вам групп. МедианаМе – вариант, расположенный посередине ранжированного ряда. Если n четное, то Ме = полусумме центральных вариантов. Мода Мо – наиболее часто встречающийся вариант. Вариационный размах RR=Xmax-Xmin. Дисперсияs^2 - средняя арифметическая квадратов отклонений вариантов от их средней арифметической: s^2=(∑(xi-x среднее)^2 *ni)\n= ∑( xi-x среднее)wi. Среднее квадратическое отклонение s.Св-ва дисперсии: 1) s^2 постоянной=0. 2)Если все варианты увеличить (уменьшить) в одно и то же число к раз, то дисперсия увеличится (уменьшится) в к^2 раз. 3)Если все варианты увеличить (уменьшить) на одно и то же число, то дисперсия не изменится. 4) . Нач момент порядка k Центр момент порядка k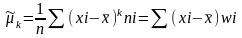 . Коэфассиметрии Эксцесс