39, Теорема (о предельном переходе под знаком интеграла).

Пусть - последовательность интегрируемых функций на множестве 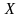и на . Тогда функция интегрируема и

Доказательство.

Так как последовательность равномерно сходится к , то для (5)

Следовательно, функция интегрируема и

Рассмотрим разность

Таким образом, для

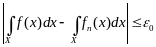
Это значит, что

Теорема Лебега (о предельном переходе).

Пусть - последовательность измеримых функций на множестве , которые почти всюду сходятся к функции , т.е. . И пусть существует такая интегрируемая функция на , что . Тогда функция интегрируема и возможен предельный переход, т.е. .

40, Теорема (о прямом произведении полуколец)

Пусть -мера на полукольце множества ,

-мера на полукольце множества

Определим - прямое произведение полуколец и .

Теорема (о прямом произведении полуколец).

Прямое произведение полуколец является полукольцом.

Доказательство.

Пусть - полукольцо подмножеств множества ,

- полукольцо подмножеств множества

Пусть - прямое произведение.

Докажем, что S является полукольцом подмножеств множества .

I. Пусть . Докажем, что .

Т.к. , то можем записать .

Аналогично , где , .

Имеем .

Т.к. - полукольцо, то

Т.к. - полукольцо, то

Тогда .

II. Пусть , где , и , тогда

Получаем, что

В последних равенствах , т.к. .

42 Теорема Фубини. Теорема Тонелли.

Интеграл от функции называется интегралом Лебега:

, иногда пишут .

Будем рассматривать интегралы

и .

Эти интегралы называют повторными.

Теорема Фубини.

Если функция интегрируема по мере , тогда существует двойной интеграл .

Теорема Тонелли.

Если функция измерима по мере и существует хотя бы один из повторных интегралов или , тогда функция интегрируема по мере и существует двойной интеграл .