35. Пространство

- фактор–пространство пространства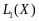 по подпространству .

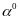является векторным пространством. В этом пространстве введём метрику : .

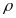Проверим аксиомы метрики:

1) 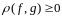, выполняется, так как .

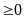Пусть . Тогда

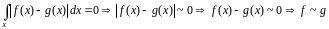Класс, который содержит функцию , обозначим .

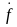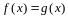, значит функции в пространстве

2) По определению следует , что .

3) .

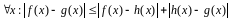По свойству линейности и монотонности интеграла имеем:

.

Таким образом, введённая функция удовлетворяет всем аксиомам метрики, то есть является метрикой на .

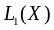36. Пространство

Рассмотрим - пространство функций, квадратично интегрируемых на множестве , то есть

Это пространство факторизуется: .

Обозначим 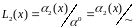- фактор – множество по 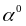и также является фактор-множеством .

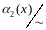Теорема (неравенство Буняковского-Коши-Шварца).

Пусть f и g – квадратично интегрируемые функции на , тогда справедливо неравенство:

В пространстве 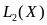введем метрику:

Так как 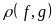, удовлетворяет всем аксиомам метрики:

1. , т.к. подынтегральное выражение

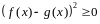
2. , т.к.

3.

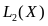То, получили, что является метрикой, которая превращает в метрическое пространство.

37. Пространство

Рассмотрим пространство 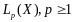- пространство функций, интегрируемых в -ой степени.

- метрика, которая превращает в метрическое пространство.

38. Пространство

Рассмотрим пространство 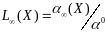- пространство почти всюду ограниченных функций, т.е. определено как

,т.е.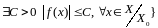

Наименьшее из значений С, удовлетворяющих этим условиям, называется существенной границей и обозначается

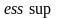
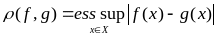
41, Тензорное произведение мер.

Напомним, что если есть две функции и 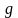, то можно построить тензорное произведение этих функций: .

Операция называется тензорным произведением.

Пусть даны два пространства с мерой ,

Пусть -мера на полукольце множества , -мера на полукольце множества

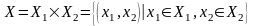
Определим 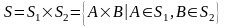- прямое произведение полуколец и .

Определение. Пусть - мера на полукольце , - мера на полукольце и -полукольцо. Определим на полукольце S - меру 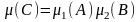, где 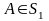, 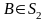. Тогда - называется тензорным произведением и и записывается следующим образом: .

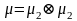Теорема (о тензорном произведении мер).

Тензорным произведение мер является мерой, т.е. если - мера на пространстве , а - мера на пространстве , то является мерой на пространстве .

Доказательство.

I. Возьмем 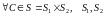-полукольца множеств на пространствах соответственно. Тогда представляется в виде:

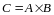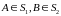, где , тогда .

II. Докажем, что если 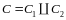, где , тогда

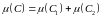- это свойство аддитивности меры .

Для этого рассмотрим характеристическую функцию

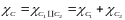(1)

Т.к. , где 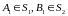, тогда

(2)

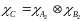Аналогично, , где , тогда (3)

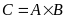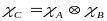Поскольку , то (4)

Подставляем (2), (3), (4) в (1):

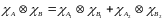(5)

Т.к. характеристическая функция множеств является интегрируемой, то можно проинтегрировать равенство по :

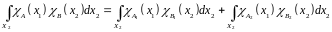Получаем:

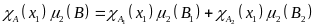(6)

Полученное соотношение (6) проинтегрируем по множеству :

Получаем:

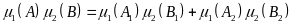
Из этого по определению следует: .

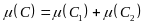Таким образом, доказали аддитивность .

Итак, - неотрицательна и аддитивна, значит является мерой.