28)Определение измер. Функции и её свойства

Определение. Функция , определенная на множестве , называется измеримой, если существует последовательность ступенчатых функций, которая равномерно сходится к на множестве .

Совокупность всех измеримых функций будем обозначать .

Свойства измеримых функций.

1. Произведение любого числа на измеримую функцию есть измеримая функция, т.е.

.

Действительно, т.к. . Умножим обе части соотношения на , получим . По свойству 1 ступенчатых функций .

2. Сумма двух измеримых функций является измеримой функцией, т.е. .

Действительно, т.к. , то

Суммируя эти соотношения, получаем:

.

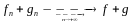По свойству 2 ступенчатых функций .

3. Линейная комбинация измеримых функций является измеримой функцией, т.е.

.

Доказательство следует из свойств 1 и 2.

Это свойство значит, что совокупность всех измеримых функций образует векторное (линейное) пространство над полем .

4. Произведение измеримых функций является измеримой функцией, т.е.

29. Теорема (о лебеговских множествах измеримых функций).

Все лебеговские множества измеримых функций измеримы.

Доказательство.

Пусть , т.е. для (1)

Из (1) следует (2)

Возьмем .

Положим .

Подставим данное равенство в (2):

(3)

Положим и подставим в (3)

(4)

Итак, мы взяли произвольное и доказали (4). Это значит, что .

Докажем обратное включение.

Возьмем

Перейдем к пределу при :

.

Таким образом, доказали (6)

Из (5) и (6) следует равенство (7)

30. Теорема (об измеримости функций).

Если все лебеговские множества функций измеримы, то и функция измерима.

Доказательство.

Пусть .

Докажем, что , т.е. что .

Зафиксируем и построим ступенчатую функцию . Для этого построим множество

С другой стороны множество образует множество

.

Из построения следует, что

.

31. Теорема (о пределе последовательности измеримых функций).

Поточечный предел последовательности измеримых функций является измеримой функцией: .

Доказательство.

Возьмём произвольное и рассмотрим Лебеговское множество . Как следует из замечания к теореме «О лебеговских множествах измеримых функций» необходимо и достаточно доказать, что .

Таким образом, мы получили, что .

32. Теорема (о сходящейся почти всюду последовательности измеримых функций).

Если последовательность измеримых функций , то функция измерима.

Доказательство.

Так как по условию, то

.

Возьмём произвольную и рассмотрим Лебеговское множество , его можно представить в виде: . Так как сходится на 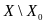к и каждая функция измерима, то , , поэтому .

Таким образом

. Следовательно, , то есть любое Лебеговское множество функции измеримо. Применим теорему «Об измеримости функции». Тогда получим, что функция измерима.

33. Определение. Функция называется интегрируемой (по Лебегу), если существует последовательность 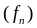интегрируемых ступенчатых функций, которые равномерно сходятся к функции : на .

Совокупность всех интегрируемых функций обозначается .

Свойства интегрируемых функций.

1. , :

.

2.

, на .

3. , то есть .

34. Определение. Интегралом Лебега от интегрируемой функции называется число, обозначаемое

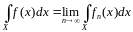(1)

где 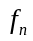- последовательность ступенчатых интегрируемых функций, равномерно сходящихся к функции .

Свойства интеграла Лебега.

1. .

2. .

3. Линейность.

.

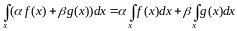4. .

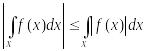5. Монотонность.

.

6. .

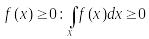7. Если функция ограничена на пространстве конечной меры, т.е. измерима, то . Если функция измерима, то . Если ограничена, то , которая принимает конечное число значений.