22) Теорема (о - аддитивности распространения меры).

Пусть мера - -аддитивная мера на полукольце 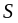, тогда ее распространение на кольцо будет тоже - аддитивной мерой.

Доказательство.

Пусть 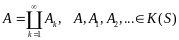Докажем, что

, где

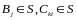т.к. и 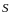– полукольцо, то

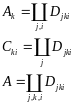
Воспользуемся определением распространения меры:

23)Определение внешней меры. Теорема об 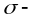полуаддитивности внешней меры

Определение. Пусть – произвольное множество, и пусть 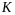– алгебра, т.е. 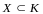, на которой задана аддитивная мера 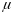. Тогда внешней мерой множества называется число

. Отображение называется внешней мерой.

Теорема (об полуаддитивности внешней меры).

Пусть множество , тогда , где произвольные множества. Доказательство:

Возьмем произвольное 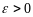и построим 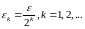Внешняя мера множества . По определению это

.

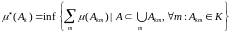По определению inf будем иметь, что (1)

Тогда

.

Т.е. мы доказали, что 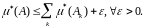(2)

Устремляя 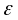к нулю, получим требуемое неравенство

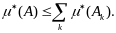
24 Измеримые множества и их свойства

Говорят, что последовательность функций , заданных на множестве равномерно сходится к 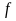, если

.

В этом случае пишут: .

Определение. Функция , определенная на множестве , называется измеримой, если существует последовательность ступенчатых функций, которая равномерно сходится к 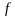на множестве .

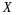Совокупность всех измеримых функций будем обозначать .

Свойства измеримых функций.

1. Произведение любого числа на измеримую функцию есть измеримая функция, т.е.

.

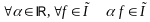2. Сумма двух измеримых функций является измеримой функцией, т.е. .

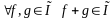3. Линейная комбинация измеримых функций является измеримой функцией, т.е.

.

4. Произведение измеримых функций является измеримой функцией, т.е.

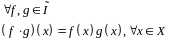
5. Если 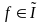, то модуль измеримой функции является измеримой функцией, т.е. .

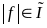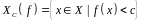Определение. Пусть функция определим множество - Лебеговское множество.

Теорема (о лебеговских множествах ступенчатых функций).

Все лебеговские множества ступенчатых функций измеримы.

25 Ступенчатые функции и их свойства.Пример

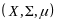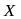Определение. Пусть - пространство с мерой. Функция , заданная на множестве , называется ступенчатой, если можно представить в виде:.

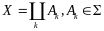
Совокупность всех ступенчатых функций будем обозначать .

Свойства ступенчатых функций.

1. Произведение любого числа на ступенчатую функцию есть ступенчатая функция, т.е.

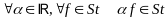
2. Сумма двух ступенчатых функций является ступенчатой функцией, т.е. .

3. Линейная комбинация ступенчатых функций является ступенчатой функцией, т.е.

.

4. Произведение ступенчатых функций является ступенчатой функцией, т.е.

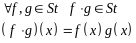
5. Если 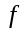-ступенчатая функция, т.е. 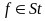, то модуль ступенчатой функции является ступенчатой функцией, т.е. .

Пример функция Дирихле, функция Хевисайда

26 Интегрируемая ступенчатая функция

Определение. Ступенчатая функция называется интегрируемой, если ряд 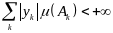, т.е. сходится.

Это означает абсолютную сходимость ряда .

Если ступенчатая функция интегрируема, то модуль ее интегрируем.

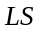- множество интегрируемых ступенчатых функций.

Свойства интегрируемых ступенчатых функций.

1. Произведение любого числа на интегрируемую ступенчатую функцию есть интегрируемая ступенчатая функция, т.е.

.

2. Сумма двух интегрируемых ступенчатых функций является интегрируемой ступенчатой функцией, т.е. .

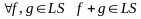3. Линейная комбинация интегрируемых ступенчатых функций является интегрируемой ступенчатой функцией, т.е.

.

4. Если , то .

27 ИНТЕГРАЛ ОТ ИНТЕГРИРУЕМОЙ СТУПЕНЧАТОЙ ФУНКЦИИ

Определение. Интегралом от интегрируемой ступенчатой функции называется число, которое обозначается и определяется .

Свойства интеграла.

1.

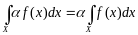
2.

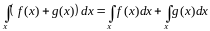
3.

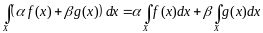
Интеграл является линейным функционалом.

4.

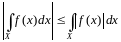
Примеры.

1. пусть , - пространство с конечной мерой, т.е.

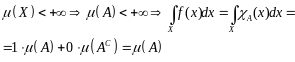
Т.к.

2. рассмотрим функцию Дирихле

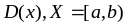
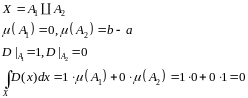
Из примера 1) следует, что .