12, Обобщенно сжимающее пространствро
Определение.
Отображение
с
метрикой
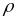называется обобщенно-сжимающим
отображением,
если
-
сжимающее отображение, где
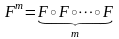
14. Функция Дирихле
Рассмотрим
функцию Дирихле
Составим
для этой функции интегральную сумму.
Для простоты будем рассматривать
:
Отрезок
разбивается на
частей и получаем
отрезков вида
.
По этому разбиению строим сумму
.
Определяется
ранг разбиения
.
Интеграл Римана – это предел интегральных сумм, когда ранг разбиения стремится к нулю.
Если
,
тогда
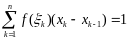и
.
Если
,
тогда
.
Итак получаем противоречие:
15. Кольцо и полукольцо множеств. Примеры.
Определение.
Совокупность
подмножеств множества
называется кольцом
,
если:
1.
2.
Определение.
Система
подмножеств S
множества
,
которая содержится в
,
называется полукольцом, если:
1)
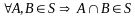
2)
Примеры полуколец.
Пусть
и
.
Пересечение полуинтервалов –
полуинтервал. Множество полуинтервалов
образуют полукольцо.Пусть
и
-
двумерная ячейка.
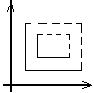
Пусть
и
-
-мерная
ячейка.
16. Теорема (о кольце, порожденном полукольцом).
Если S – полукольцо то K(s) – кольцо.
Доказательство.
Пусть
,
где
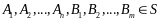
Рассмотрим
и покажем, что
I.
Покажем,
что
Будем доказывать методом математической индукции (индукцию проводим по ):
Если
,
то
,
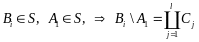где
Пусть наше утверждение
верно
при
,
т.е.
Покажем, что оно справедливо и для :
тогда можно
записать:
Таким образом, доказали, что
из
справедливо:
II. Рассмотрим
Т.о.
показали, что
Тогда
Мы
доказали, что
и
-- кольцо.
17. Определение меры. Примеры мер.
Определение.
Пусть
,
пусть любому
,
сопоставлено число
,
причем выполнены условия, называемые
аксиомами меры:
1)
(неотрицательность)
2)
,
,
то
(аддитивность)
Тогда
называется мерой
множества
,
а сама функция
называется мерой.
Пример.
1)
,
то
(мера
равна длине интервала)
2)
,
то площадь прямоугольника:
-
3)
,
то
18. Продолжение меры с полукольца на кольцо.
Пусть мера m задана на полукольце Н, М – кольцо, минимальное над Н.
Лемма.
Пусть
– конечные разложения
Тогда
Теорема
1. Пусть
– произвольное продолжение меры m
с полукольца H
на некоторый класс
.
Если
то
(единственность продолжения в пределах
кольца M).
Теорема 2.Если мера m счетно-аддитивна, то и её продолжение с полукольца H на кольцо M, минимальное над H, также является счетно-аддитивной мерой.
19. Свойства меры на порожденном кольце.
1)
2) Монотонность меры.
3) Свойство «субаддитивности».
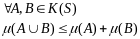
4)
5)
Если
,
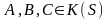то
20. Введение метрики на кольце множеств.
Введем
в пространстве
(элементы этого пространства - множества),
метрику
Проверим выполнение всех аксиом меры.
1.
,
т.к.
2.
,
применим к обеим частям меру
,
получаем
3.
21) σ-аддитивная мера. Пример атамарной
Определение.
Мера
,
заданная на
,
называется
- аддитивной, если
;
причем
,
то
.
Отметим, что все меры в рассматриваемых примерах являются - аддитивными
[ )[ )
Примеры.
1. Атамарные меры.
,
возьмем точку
и определим меру
:
Тогда
называется атамарной мерой, сосредоточенной
в точке
.