1) Определение и свойства метрических пространств

Опр. Пусть Х – произвольное мн-во и пусть любым двум элементам x,y X сопоставлено неотрицательное число p(x,y) 0, которое обладает следующими свойствами: 1) p(x,y)=0 <=> x=y ( аксиома отделимости) 2) p(x,y)= p(y,x), x,y X ( аксиома симметрии) 3) p(x,z) p(x,y)+ p(y,z) x,y 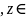X (аксиома треугольника) Аксиомы 1-3 наз. аксиомами метрического пр-ва, p(x,y) наз. метрикой на мн-ве Х , а мн-во Х на котором задана метрика наз. метрическим пр-м

2)Сх-ся и фундаментальные послед-ти метрических пр-в, полные метрические пр-ва.

Опр. Послед-ть наз. сходящейся последовательностью в метрическом пр-ве Х если > 0 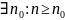p(x_n,x) . Элемент х наз. пределом послед-ти {x_n}

Опр. Послед-ть {x_n} в метрическом пр-ве Х наз. фундаментальной, если > 0 p(x_n,x_m)

Опр. Метрическое пр-во Х, в котором любая фундаментальная послед-ть сх-ся наз. полным метрическим пространством.

3)Примеры метрических пр-в 1-8

1. Пр-во R всех действительных чисел с метрикой. p(x,y)=|x-y| (x,y )

2. Пр-во С всех комплексных чисел с метрикой. p(x,y)=|x-y| (x,y )

3. Произвольное непустое мн-во Х с метрикой. p(x,y) (x,y )

4. . Пр-во (n ) всех конечных последоват-й, состоящих из n чисел с классической евклидовой метрикой p(x,y)= (x = (x₁,x₂…x_n), )

5. Пр-во всех конечных последоват-й, состоящих из n чисел с метрикой p(x,y)= (x = (x₁,x₂…x_n), )

6. . Пр-во (p ) всех конечных последов-й, состоящих из n чисел с метрикой p(x,y)=

7. Пр-во (p ) всех числовых последов-й, суммируемых в p-й степени, т.е. таких числовых послед-й х=(х_m) , что ряд сх-ся, с метрикой

p(x,y)= (x,y )

8.Пр-во всех ограниченных числовых последовательностей, с метрикой

p(x,y)= (x,y )

4)Примеры метрических пр-в 9-16

9. Пр-во всех С сх-ся числовых последовательностей, с метрикой

10.Пр-во С₀ всех бесконечно малых числовых последовательностей с метрикой, опред формулой: p(x,y)= (x,y )

11. Пр-во S всех числовых последовательностей с метрикой p(x,y)= (x=(x_n), y=(y_n) )

12.Пр-во С[a,b] всех непрерывных на [a,b] ф-ций с метрикой p(x,y)= (x,y С[a,b])

13. Пр-во С^k[a,b] всех к раз непрерывных диф. на [a,b] ф-ций с метрикой p(x,y)= (x,y С^k[a,b])

14. Пр-во [a,b] всех непрерывных диф. на [a,b] ф-ций с метрикой

p(x,y)=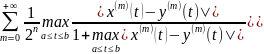 (x,y [a,b])

15. Пр-во C(R) всех непр. ф-ций на числовой оси R с метрикой p(x,y)= (x,y )

16. Пр-во Е всех беск. диф. на всей числовой оси R ф-ций с метрикой

p(x,y)= (x,y )

5. Топология мп

Если точка принадлежит открытому множеству, то существует шар, который содержится в данном множестве.

Совокупность всех открытых множеств метрического пространства называется топологией этого пространства и обозначается , когда фиксировано, то .

Топология метрического пространства обладает следующими характеристическими свойствами:

1) , т.е. пустое множество и пространство - открытое множество.

2) Объединение любого семейства множеств из принадлежит , т.е .

Доказательство.

Возьмем точку . Нам дано, что . Т.к. - произвольная точка, то любая точка является внутренней, следовательно, множество открыто, т.е. .

3) Пересечение любого конечного семейства из принадлежит , т.е.