Линейные ограниченные операторы, нормы.

Пусть X,Y – БП. Оператор н-ся линейным, если D(A) – ЛМ и образ. Линейный оператор н-ся ограниченным, если const , что справ-во н-во: (1) Нормой оператора А н-ся inf всех const-т М таких, что вып-ся

Теорема. (2). Д-во: . Положим Из (1) . Полож. противоп-е нер-во. По опр-ю inf имеем …( что-то набо было самим написать, я хрен знаю чё!!!)

Замеч-е. Пусть вып-но нер-во (1), т.е. 1.Если , уменьшить ||A|| нельзя. Д-во: ЧТД 2.Если , если то ||A||=M. 3. Либо , такая что , то ||A||=M.

Линейные-непрерывные операторы.

Лин-й оп-р А н-ся непрер-м в , если или . Оп-р н-ся непрер-м, если он непр-й в кажд. точке

Теорема. Из непрер-ти лин. оп-ра в 0 след-т его непрер-ть в Д-во: Пусть А – непрер. в 0, т.е. . Пусть -произв. т. из Х, . Тогда найдем . Получим: ЧТД

Теорема. Для того, что бы лин. опер-р был ограничен н.и.д.,ч. он был непрерывн. Д-во: 1) А – огр А – непр. 2) А – непрер. А – огран. ПП А-неогран., т.е. (!) Обюозначим , - противоречие. ЧТД.

Норма оператора Фредгольма.

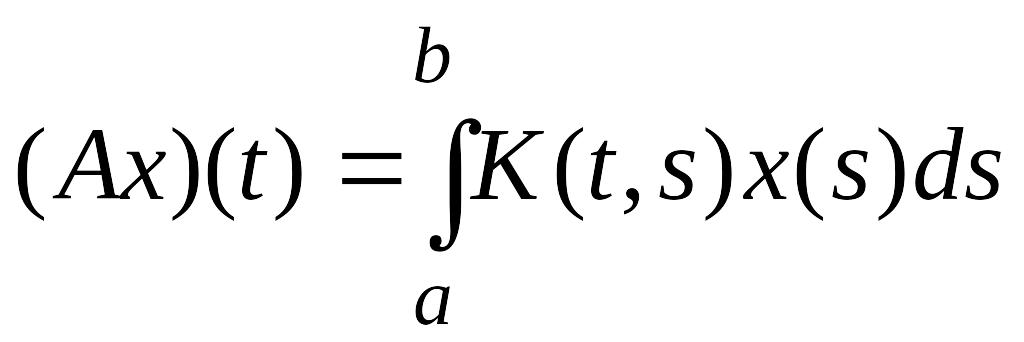
Ядро K(t,s)-непрер-но; . 1) Пусть ф-ция K(t,s) не меняет знак, т.е. не обращается в 0. Выберем 2) Пусть K(t₀,s) меняет знак, тогда x₀(s) – разрывная ф-ция. Найти элемент на кот. достигается р-во неудается. и , т.о.

Пространство линейных ограниченных операторов.

Пусть X,Y – НП. И А,В,С – лин. огр. оп-ры из X в Y. Тогда м. определить сумму. , тогда мн-во образует ЛП. или . (проверим все аксиомы…) Т.о. мн-во лин-х огр-х оп-в явл-ся НП и обозначается «эль»

Теорема. Если Х – НП, У – БП -БП.

Равномерная сх-ть послед-ти опер-в.

Послед-ть равномерно сх-ся к А ( ), если

Теорема. Посл-ть равномерно сх-ся к опер-ру А т.и.т.т.,к. сх-ся к Ах Д-во: 1) 2) обратно: равномерно относительно . Это означ-т: п-ть равн. сх-ся. ЧТД.

Поточечная сх-ть.

Посл-ть (сильно, поточечно), если , т.е.

Теорема. Если посл-ть { } равномерно сх-ся к оп-ру А, то она сх-ся и сильно (поточечно). Обратное неверно. Д-во: Обратное не верно: Пусть Покаж., что , как отрезок сх-ся ряда; - по норме не сх-ся. ЧТД.

Линейные ограниченные функционалы.

Х – БП, н-ся функционалом. Функционалом н-ся лин-м и огранич-м, если и (1), и непрерывным, если

Нормой функционала н-ся

Теорема Рисса (об общем виде лин-го огран-го функ-ла в ГП). Пусть Н – ГП. Для любого лин. огр. ф-ла (2), при этом Д-во: Рассм мн-во 0й функ-ла f; L – ЛМ и замкн., т.е. L – ЛП. , . Пусть - пред. т. L, т.е. В силу непрер-ти f значит L – подпр-во в Н. . Возьмем и рассм. элемент . Покажем, что , т.е. Поэтому скал-е произвед-е или . Покажем единственность: ПП: . По функционалу f соотв-т ед-й эл-т a ||f||=a. ЧТД.

Теорема Хана-Банаха и следствия из неё.

Пусть - НП. Функционал н-ся продолжением ф-ла , если .

Теорема Х – Б. Всякий лин-й огранич. ф-л f заданный на можно продолжить на всем Х с сохранением нормы.

Следствие 1. пусть Х – НП . Сущ-т лин. (непрер.) огр. ф-л такой, что

Следствие 2. Пусть Х – НП. . Тогда сущ-т лин.-непрер-й такой, что - теорема об отделимости.

Сопряженные операторы.

Пусть Н – ГП и опер-р - лин. огр. и пусть произв. эл-т. Рассм-м функц-л - лин. ф-л. Покажем, что он ограничен . По Теор. Рисса или . Т.е. .

Оператор н-ся сопряженным к оператору А. (1)

Свойства сопр-х операторов: 1. 2. 3. 4. 5. Д-во: 1) ЧТД. 2),3) – аналогично 4) 5) -огранич. Устраним обратное нер-во. ЧТД.

Теорема. Оператором сопряженным к оператору Фредгольма с ядром K(t,s) явл-ся опер-р Фредгольма Д-во: А*-? , ЧТД.

Оп-р А н-ся самосопр-м, если А*=А, и норм-м, если A*A=AA*

Замеч-е. Если А самосопр-й оператор, то

Утв-е. Если А*=А, то число (Ах,х) – вещественное. Д-во: ЧТД.

Оператор ортогонального проектирования.

Пусть Н – ГП и , т.е. . Тогда (м. поставить в соответствие ортогональную проекцию), т.е. задан оператор ортогональн. проектир-я. Px=y

Св-ва ортопроектора: 1) Р – лин-й оп-р Д-во: ЧТД. 2) ||P||=1 Д-во: По Th. Пифагора ЧТД. 3) P*=P Д-во: ЧТД. 4) Д-во: ЧТД.

Теорема. Пусть А – лин. огр-й самосопр-й оп-р такой, что . Тогда оператор А – оператор ортогонального проектир-я на некоторое подпр-во Д-во: Рассм. , L – подпр-во = ЛМ+замкнут. - пред-я т. L, тогда А – проектор Н на L. Покажем ЧТД.

Обратные операторы

X,Y-нормированные пр-ва. A:D(A)cX→R(A)cY; R(A)={yєY: сущ хєD(A):Ax=y}; KerA={xєD(A):Ax=0}-ядро.

Теорема: Оп-р А взаимно-однозначен, если KerA={0}. Док-во: 1)Пусть КеrА={0}. ПП: оп-р не взаимно-однозначен. Сущ x₁,x_2: Ax₁=y, Ax₂=y. Вычтем A(x₁-x₂)=0; x₁-x₂єKerA{0}=>x₁=x₂ 2)Обратно:пусть А-взаимно-однознач. Пусть zє KerA=>Az=0 пусть Ax=y; A(x+z)=Ax+Az=y. Это противоречит взаимной однозначности =>z=0. ЧТД.

Пусть А-взаим-однознач yєR(A)→xєD(A)значит определён обратный оператор A^-1:R(A)→D(A); A^-1y=x такой, что Ax=y.

Линейность. Теорема. Оп-р, обратный к линейному линейный. Док-во: A(α x₁ +β x₂)=αA x₁ +βA x₂; Ax₁ = y_1, Ax₂=y₂, x₁=A^-1y₁, x₂=A^-1y₂. Из первого равенства: A(α₁ x₁ +β₁ x₂)=α y₁+βy₂; α x₁ +β x₂=A ^-1(α x₁ +β x₂); αA ^-1 y₁+βA ^-1 y₂=>обратный оп-р линейный. ЧТД

Теорема:Оп-р A ^-1 сущ и ограничен на R(A) т.и.т.т.,к. сущ llAxll>=mllxll (1) Док-во:1)Пусть (1)выполнено, тогда KerA={0}=>сущ A ^-1: R(A) → D(A);(1)эквивалентно llyll>=mll A ^-1yll; ll A ^-1yll<=1/mllyll 2)Обратно: пусть сущ A ^-1 ограниченный ll A ^-1yll<=Mllyll; yєR(A); y=Ax, тогда A ^-1y=x; llxll<=MllAxll =>m=1/M ЧТД.

Оп-р А наз непрерывно-обратимым, если обратный оп-р сущ, определён на всём Y и ограничен. A:X→Y, A^-1:X→Y

Теорема Банаха: Лин. огранич оп-р A:X→Y непрерывно-обратим т и тт, когда он отображает XнаY взаимно-однозначно. То есть:1) R(A)=Y; 2)KerA={0} (Без док-ва)

или ур-е Ax=y им. реш-е; однор-е ур-е им. только 0е реш-е.

Замечание: В конечномерном пр-ве для непрерыв обратимости оп-ра А достаточно выполнение лишь одного из условий теоремы Банаха.Т.е. если dimX=dimY=n, то R(A)=Y KerA={0}

Решение интегральных уравнений с вырожденным ядром

(1) Ядро назыв вырожденным, если оно представимо в виде суммы: K(t,s)=_k=1∑ⁿ p_k(t)q_k(s) подставим в (1); x(t)= _k=1∑ⁿp_k(t) q_k(s)x(s)ds+f(t) тогда x(t)= _k=1∑ⁿc_kp_k(t)+f(t) (2) q_j(t)x(t)dt= _k=1∑ⁿc_k p_kq_jdt+ f(t)q_j(t)dt; c_j- _k=1∑ⁿc_k(p_k,q_j)=(f,q_j) j=1…n (3).

Теорема: 1)Если алгебраическая система (3) имеет единств решение с₁, ..с_n, тогда ур-е (1) имеет единств решение, которое выписывается по ф-ле (2); 2)Если система (3) не имеет решений, то ур-е (1)не имеет решений 3)Если система (3) имеет бесчисленное множество решений, то и ур-е (1) имеет бесчисл мн-во решений.

Левые и правые обратные операторы

АєL(X,Y); A ^-1_r єL(Y,X) наз правым обратным к оп-ру А, если А A ^-1_r=I_y→_y (для любого yєY AA ^-1_ry=y); A ^-1_lєL(Y,X) наз левым обратным к оп-ру А, если A ^-1_lA=I_x→_x (для любого yєY A ^-1_lAx=x).

Утвержд1 Если сущ правый обратный, то ур-е Ax=y имеет решение. Док-во: x=A ^-1_ry; Ax=AA ^-1_ry=y ЧТД.

Утвержд2 Если сущ лев обратный, то ур-е Ax=y может иметь не более одного решения Док-во: Предп противное Ax₁=y Ax₂=y вычтем A(x₁-x₂)=0 применим лев обратный A ^-1_lA(x₁-x₂)= A ^-1_l0; x₁-x₂=0=> x₁=x₂ ЧТД.

Теорема Пусть A:X →Y и сущ A ^-1_r єL(Y,X) и A ^-1_l єL(Y,X), тогда A ^-1_r =A ^-1_l= A ^-1(А непрер обратим). Док-во: Тк сущ A ^-1_r то ур-е Ax=y имеет решение для любого y єY=>R(A)=Y. Тк сущ A ^-1_l, то Ker={0}=> выполним оба условия теор Банаха=> cущ обратный A ^-1 єL(Y,X)=>A A ^-1= A ^-1A=I => A ^-1= A ^-1_r; A ^-1= A ^-1_l ЧТД.

Существование (I-a)-1

Теорема Пусть A єL(X) и llAll<=q<1, X-БП. Тогда оп-р (I-A) непрер обратим и (I-A)^-1=_k=0∑^∞A^k (1) и справедлива оценка ll(I-A)^-1ll<=1/(1-llAll) (2) Док-во: Покажем, что ряд _k=0∑^∞A^k<∞ ll A^kll=llAA…All<=ll A^kll<=q^k .Т.к. q<1, то по признаку Вейершт ряд сх-ся. Послед-сть частичных сумм S_n= _k=0∑ⁿ A^k →s/ n →∞ (I-A)S_n=(I-A)(I+A+…+Aⁿ) =I+A+..+Aⁿ-A-..-Aⁿ-Aⁿ⁺¹=I-Aⁿ⁺¹ то есть (I-A)S_n=I-Aⁿ⁺¹(3) Тк llAll<=q<1, то llAⁿ⁺¹ll→0, n→∞ переходя в (3) к пределу: (I-A)S=I Аналогично S_n(I-A)=I-Aⁿ⁺¹ S(I-A)=I, n→∞ то есть s явл и лев и прав обратным=>S- настоящий обратный S=(I-A)^-1_r; S=(I-A)^-1_l Имеем ll(I-A)^-1ll<=_k=1∑^∞llA^kll<=_k=0∑^∞llAll^k=1/(1-llAll) ЧТД.

Элементы спектральной теории линейных операторов

A:X→X, где Х-компл банахово пр-во. λєС наз регулярной точкой (значением) оп-ра А, если оп-р (A-λI) непрерыв обратим. Множ всех регулярных точек образует резольвентное множество ρ(А) ; ρ(А)={ λ єC: (A-λI)^-1єL(X)} дополнение к резольвентному множеству наз спектром оп-ра А δ(A)=C\ρ(А); (A-λI)^-1=R(A; λ)-резольвента оп-ра А;

λєρ(А), если выполн оба условия теоремы Банаха для оп-ра (A-λI). То есть если 1) Ker(A-λI)={0}; 2)R(A-λI)=X ;

λє δ(A), если не выполнено одно из условий теор Банаха 1)Если не выполнено 1-ое условие: сущ x≠0: (A-λI)x=0 или Ax= λx. В этом случае λ-собств значение, а x-соотв собств вектор δ_α(A)={ λ єC: сущ x≠0:Ax= λx}-дискретный спектр А. Тк в конечномерном пр-ве для непрер обратимости оп-ра А достаточно выполнение лишь одного из условий теор Банаха, то в конечномерном пр-ве спектр оп-ра Асостоит только из собств значений 2)Если не выполн условие 2: R (A-λI) ≠X, но плотно в нём. То есть R(A-λI)=X. Такие λ явл точками непрерыв спектра. δ_с(A)={ λєC: R(A-λI) ≠X,но дополнение R(A-λI)=X} λ наз точками остаточного спектра, если: дополнение R(A-λI) ≠X не плотно в Х δ_r(A)={ λєC: дополнениеR(A-λI) ≠X} Таким образом δ(A)= δ_α(A) Uδ_с(A) Uδ_r(A)

Св-ва резольвентного мн-ва

Теорема. и , (1) - ряд Неймана Д-во. , - непр. обрат. т.к. ЧТД.

Теорема. Резольвентное мн-во открыто. Д-во.

То непр. обратим как произведение двух обр. операторов.

Св-ва спектра

Следствие 1. Спектр оператора А есть замкн. мн-во содерж-еся в круге с центром в нач. коорд. и радиусом т.е. Можно показать, что не пусто.

Теорема. Пусть Собств. вектора, отвечающие различным соб. знач. опер. А линейно независимы. Д-во. Пусть - соб. знач. оператора А, а -соб.вект. им отвечающие, причём . Покажем, что векторы лин. нез. k=1 : - лин. нез. Предположим, что - лин. нез.

Т.к. - лин. нез., то тогда из (5) - лин. нез. ЧТД.

Замеч-е. Без ограничения общности, м. считать, что с.в. отвеч-е различ. с.з. ортогональны (прим процесс ортогонализации).

Теорема. Собственные числа самосопр. опер. вещественны , Х=H. Д-во. Пусть -с.ч. опер. A т.е. , ЧТД.

Теорема. С.в. самосопр. опер, отв. рзличным с.з. ортогональны,Х=H. Д-во. ЧТД.

Спектральный радиус линейного оператора (Вольтера)

Спектр. радиусом наз. Радиус максимального круга сод. спектр т.е.

Справедлива формула Коши-Адамара:

Теорема. Если Д-во. Покажем, что если ; По индукции получаем По формуле Коши-Адамара: ЧТД.

Tеорема. Если Следствие. оператора Вольтера.Замечание. Т.к. оп. Вольтера, то оп. Вольтера не имеет огранич-го обратного.

Компактные множества

Х-БП. Мн-во наз предкомпактным если из любой посл. можно выделить фундамент. Т.к. Х-БП т.ч. если то мн-во наз. компактным.

!!! В бесконечномерном пр-ве теор. Больцана – Вейштрасса не верна.

Ограниченность предкомпактного мн-ва.

Теорема. Всякое предкомпактное мн-во ограничено. Д-во. Предположим противное ПП т.к. К не огр. Т.о. мы построили послед. Покажем, что из нельзя выделить сходящуюся подпоследовательность : Пусть n>m Из (*) Из этой послед. Нельзя выделить сходящуюся подпоследовательность. Против-е. ЧТД.

Функционалы на компактных множествах

Теорема Вейштрасса 1. Пусть К-комп. - непр. функционал, тогда он ограничен на К. Д-во. Покажем сначала ,что сущ-т ,ПП: такой константы не существует т.е. . Т.к. К-комп. т.е. из м. выделить сходящуюся подп-ть ,то Т.к. f. функционал , то , что против. (1) . Т.е. функция ограничена сверху, аналогично, ограничена снизу Ф-л ограничен. ЧТД.

Теорема Вейштрасса 2. Пусть К-компактное мн-во в Х -непрер. ф-ия, тогда она достигает своей точной верхней и нижней граней т.е. Д-во. По опр Sup . Из последовательности можно выделить сход. подпосл. т.ч. . В силу непрерывности функции , с другой стороны т.к. , то переходя к пределу . Аналогично и для inf. ЧТД.

Критерии предкомпактности

Теорема. В конечном-м пр-ве для того, чтобы было предкомп-ым н. и д., ч. оно было огранич-м.

Критерий Хаусдорфа.

Пусть - БП. Множество н-ся - сетью для множества , если .

Мн-во покрывается объедин-ем шаров с центрами в т-х - сети и радиусами . - сеть н-ся конечной, если она состоит из конеч. числа точек.

Теор. Хаусдорфа. Пусть - БП. Для того, чтобы было предкомп-ым необх-мо и достаточно, чтобы в конечная - сеть для . Док-во: 1) Необх-ть: Пусть - предкомпактно. Выберем произв-е >0. Возьмём точку . Если окажется что , то - сеть. Если это не так, то . Если окажется, что выполнимо , то . Если это не так, то … Продолжая этот процесс, получ. посл-ть . Если посл-ть содержит бескон. число членов, то из этой посл-ти нельзя выд-ть фунд. подпосл-ть, что противоречит предкомп-ти этот процесс на каком-то шаге оборвётся и будет построена конечная - сеть: . 2) Дост-ть: в конечная - сеть для К. Покажем, что К-предкомпактно: Возьмём . конечная - сеть. . Мн-во К покрывается объедин-ем шаров. Возьмём . Возьмём произвольную посл-ть и покажем, что из неё можно выбрать фундам. подп-ть. Т.к. шаров конечное число, а посл-ть бесконечна, то , кот. содержит бесконечное число членов этой послед-ти . . Возьмём , т.к. покрывается шарами шар радиуса , содержащий бесконечное число членов этой последовательности, т.е. . Продолжая этот процесс, мы получим послед-ть влож-х шаров и выделе-х подпосл-тей:

Р ассмотрим диагональную посл-ть и проверим, является ли она фундаментальной: Т.к. следующая посл-ть выделилась из предыдущей, то

, то

ЧТД.

Следствие: предкомпактная - сеть для К, то множество К-предкомпактно. Док-во: Пусть -предк-но. - сеть для К, т.е. . Т.к. - предкомпактное мн-во, то по теор. Хаусдорфа конечная - сеть , т.е. . Тогда - конечная - сеть для К. Действительно . По критерию Хаусдорфа мн-во К предкомпактно. ЧТД.