Пропорции Фибоначчи в природе.

Просто удивительно, сколько постоянных можно вычислить при помощи последовательности Фибоначчи, и как ее члены проявляются в огромном количестве сочетаний. Однако не будет преувеличением сказать, что это не просто игра с числами, а самое важное математическое выражение природных явлений из всех когда-либо открытых. Приводимые ниже примеры показывают некоторые интересные приложения этой математической последовательности.

Раковина.

Раковина закручена по спирали. Если ее развернуть, то получается длина, немного уступающая длине змеи. Небольшая десятисантиметровая раковина имеет спираль длиной 35 см. Cпирали очень распространены в природе. Раковина в форме спирали - форма раковины заинтересовала Архимеда и он выяснил, что увеличение длины завитков раковины – это постоянная величина и равна она 1,618.

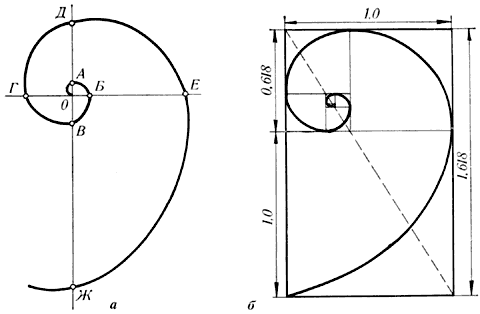
Золотые" спирали широко распространены в биологическом мире. Рога баранов, коз, антилоп и других рогатых животных растут лишь с одного конца. Этот рост осуществляется по спирали.

И не только в раковине моллюска и рогах животных можно найти спирали Фибоначчи, а во многих цветах и растениях, просто они не такие явные.

Алое многолистный Брокколи Романеско

В Университете Листера увековечили числа Фибоначчи Отмечая 25-летнюю годовщину закладки ботанического сада при Университете Листера (Великобритания), финансовые доноры заведения заказали и оплатили постройку двух новых площадок из керамической плитки, форма которых основана на знаменитых числах Фибоначчи. Найденная итальянским математиком последовательность оказывается крайне эффективной при решении проблемы размещения максимального количества элементов живого организма на минимальной площади или в минимальном объеме.

Числа Фибоначчи широко «применяются» в живой природе — начиная от расположения семечек. .Семечки у подсолнуха упорядочены в две спирали. Числа, обозначающие количество семечек в каждой из спиралей, являются членами удивительной математической последовательности в цветке подсолнуха и заканчивая расстановкой листьев на ветвях растений.

Так взяв молодую сосновую веточку, легко заметить, что хвоинки образуют две спирали, идущие слева снизу направо вверх. На многих шишках семена расположены в трех спиралях, полого навивающихся на стержень шишки. Они же расположены в пяти спиралях, круто навивающихся в противоположном направлении. В крупных шишках удается наблюдать 5 и 8 и даже 8 и 13 спиралей. Хорошо заметны такие спирали и на ананасе: обычно их бывает 8 и 13.

Растения и животные.

Еще Гете подчеркивал тенденцию природы к спиральности. Винтообразное и спиралевидное расположение листьев на ветках деревьев подметили давно. Cовместная работа ботаников и математиков пролила свет на эти удивительные явления природы. Выяснилось, что в расположении листьев на ветке семян подсолнечника, шишек сосны проявляет себя ряд Фибоначчи, а стало быть, проявляет себя закон золотого сечения. Паук плетет паутину спиралеобразно. Cпиралью закручивается ураган. Испуганное стадо северных оленей разбегается по спирали. Молекула ДНK закручена двойной спиралью. Гете называл спираль "кривой жизни". Cреди придорожных трав растет ничем не примечательное растение - цикорий. Приглядимся к нему внимательно. От основного стебля образовался отросток. Тут же расположился первый листок. Отросток делает сильный выброс в пространство, останавливается, выпускает листок, но уже короче первого, снова делает выброс в пространство, но уже меньшей силы, выпускает листок еще меньшего размера и снова выброс. Если первый выброс принять за 100 единиц, то второй равен 62 единицам, третий - 38, четвертый - 24 и т.д. Длина лепестков тоже подчинена золотой пропорции.

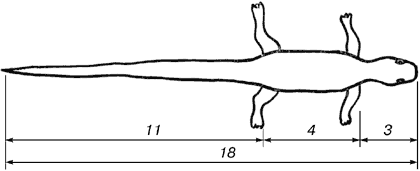
В ящерице с первого взгляда улавливаются приятные для нашего глаза пропорции - длина её хвоста так относится к длине остального тела, как 62 к 38. 0,62 к 0,38.

И в растительном, и в животном мире настойчиво пробивается формообразующая тенденция природы - симметрия относительно направления роста и движения. Здесь золотое сечение проявляется в пропорциях частей перпендикулярно к направлению роста. Природа осуществила деление на симметричные части и золотые пропорции. В частях проявляется повторение строения целого.

А если взглянуть чуть подальше, то можно разглядеть последовательность Фибоначчи в недосягаемых галактиках.

В Тихом океане имеются звезды астеридеи с 8 лучами, звезда мохнатая имеет 13 лучей. Морская звезда гелиастер (подсолнух) имеет 33 луча, а пламенистая звезда - 55. Таким образом, у многих морских звезд количество лучей задается числами Фибоначчи или близкими к ним числами.

Числа Фибоначчи и цветы.

Белая калла – 1лепесток

Молочай – 2 лепестка

Триллиум – 3 лепестка.

Лилии и ирисы имеют тоже по три лепестка.

Водосбор – 5 лепестков

По 5 лепестков есть у лютиков и живокости.

Рисунок 1. Золотое сечение

Волчья стопа – 8 лепестков

Черноглазая Сьюзан.

У Ноготков тоже 13 лепестков.

Хризантема – 21 лепесток

Некоторые астры тоже имеют по 21 лепестку.

А вот маргаритки почти всегда имеют 34, 55 либо 89 лепестков.

И тут самое время вспомнить о Золотом Сечении! Ни одни ли из самых прекрасных и гармоничных творений природы изображены на этих фотографиях? И это далеко не все. Присмотревшись, можно найти похожие закономерности во многих формах.

Конечно заявление, что все эти явление построены на последовательности Фибоначчи звучит слишком громко, но тенденция на лицо. Да и к тому же сама последовательность далека от совершенства, как и всё в этом мире.

Исследование присутствия золотого сечения в окружающей жизни

Исследование №1 «Золотое сечение в пропорциях тела человека»

Для того чтобы проверить , выполняется ли золотое сечение в пропорциях тела человека я провела исследование среди учащихся 7– 11 классов. У каждого участника были сняты мерки двух видов: мерка от верхней точки головы до талии, мерка от талии до пола. Их отношение сравнивалось с числом отношения золотого сечения.

Фамилия ,имя	От головы до талии (в)	От талии до пола (а)	а:в
1.Величенкова Света	65	103	1,584
2. Бычков Дима	68	104	1,529
3.Кондрашова Тамара	69	109	1,579
4.Андреева Лена	66	105	1,590
5. Буякова Катя	58	99	1,706
6. Букреев Саша	61	101	1,655
7.Орловская Лера	59	93	1,576
8. Бакланова Паула	65	104	1,6
9.Дударева. М	64	99	1,546
10. Клиндухов Павел	68	100	1,470
11. Артеменко Павел	68	109	1,602
12.Локтионов Костя	66	108	1,661
13. Демехин Егор	65	107	1,646
14.Новикова Ирина	60	94	1,566
15. Петин Сергей	71	107	1,507
16. Гришина Нина	69	111	1,608

Из 16-ти человек, участвовавших в исследовании наименьшее отклонение от золотого сечения среди юношей имеют: Антоненко Катя (0,023) и Грищенко Лера (0,017). Среди студентов группы 9ООП-10 Бакланова Паула и Демехин Егор имеет пропорции тела точно соответствующие золотому сечению. Те ребята, у которых пропорции тела близки к золотому сечению, Посмотрите, как они выглядят на фотографии, на мой взгляд, они действительно имеют хорошую фигуру.

Исследование№2. «Золотое сечение в природе»

Возьмём утверждение: «Рассматривая расположение листьев на общем стебле растений, можно заметить, что между каждыми двумя парами листьев (А и С) третья расположена в месте золотого сечения (точка В)».

Чтобы проверить, так ли это, я выбрала 6 различных комнатных растений:

1)Декабрист – Зигокактус

2) Алое

3)Денежное дерево - Толстянка

3)Традесканция

4)Традесканция цветущая

5) Папоротник

6)Герань - Пеларгония

Все эти растения есть в нашем техникуме, и я посчитала именно их наиболее красивыми. Сделала необходимые измерения между тройками листьев и посчитала соответствующие отношения (с точностью до тысячных).

Данные измерений и вычислений занесены в следующую таблицу:

Фамилия Имя	Рост	Расстояние до пупка	Приближённость к золотому сечению.
8 «Б» класс
Данилова Алина	170	120	1,141
Иваненко Алина	166	90	1,843
Артёменко Кирилл	170	140	1,211
Ковалевич Егор	154	90	1,714
Евкович Владимир	168	104	1,615
Андрейчик Владислав	162	130	1,246
Будило Антон	157	95	1,652
Андреенко Алина	170	106	1,603
Калыхан Карина	165	101	1,633
Шишелякина Александра	173	108	1,601
Блинова Кристина	163	98	1,663
Денисенка Анастасия	163	100	1,630
Боробьёва Марина	167	104	1,605
Пархомова Лика	154	80	1,925
Стрибук Евгений	182	111	1,639
Ефименко Дарья	170	108	1,574
8 «В» класс
Терентьева Полина	165	99	1,666
Лисицин Денис	166	104	1,596
Ковзик Максим	172	106	1,622
Патега Александр	168	104	1,615
Гапон Павел	160	80	2
Цупиков Владислав	164	102	1,623
Дубоделова Юлия	166	98	1,693
Железнякова Екатерина	161	98	1,642
Сатырева Алла	164	101	1,623
Гавриленко Татьяна	158	96	1,645
Бондаренко Александра	154	93	1,655
Зайцева Диана	163	99	1,646
Мурашкова Виктория	166	101	1,643
Чепелуева Екатерина	166	99	1,676
Гавриленко Ксения	164	99	1,656
Скорб Мария	170	104	1,634
Лендина Екатерина	160	98	1,632
Гонжурова Мария	164	100	1,640
Федоренко Валерия	157	95	1,652
Ляшук Александра	171	106	1,613

Из таблицы видно, что не все отношения получаются близкими к числу

0,618. Наиболее совершенным с точки зрения математики, оказался цветок под номером 6 герань . Следовательно, действительно расположение листьев на стебле подчиняется «божественной пропорции».

Заключение

Значение золотого сечения в современной науке очень велико. Эта пропорция используется практически во всех областях знаний. Её пытались изучить многие известные ученные и гении: Аристотель, Геродот, Леонардо Да Винчи, но никому полностью этого сделать не удалось.

В данной работе рассмотрены способы нахождения «Золотого сечения», изложены примеры, взятые из областей науки и искусства, в которых отражается эта пропорция: математика, архитектура, живопись, скульптура, ботаника.

В своей работе я хотела продемонстрировать красоту и широту «Золотого сечения» в реальной жизни. Проведенные исследования доказали, что многое в окружающем мире подчиняется правилу золотого сечения.

Мне понравилось освещать эту тему. Было интересно! Хочу дальше продолжить изучение золотого сечения.