2.5. Задачи электростатики
В зависимости от конкретных условий задачи электростатики можно условно разделить на три типа.
Задачи первого типа. Задан закон распределения потенциала в пространстве и нужно найти закон распределения свободных зарядов. Это наиболее простой тип задач и решаются они с помощью уравнений Пуассона (Лапласа).
Пример. В некоторой области пространства потенциал поля зависит только от одной координаты x декартовой системы:
.
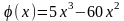Найти закон изменения плотности свободных зарядов в этом поле.
Решение. Запишем уравнение Пуассона
или
.
Поскольку 
,
то
.
Дважды дифференцируя
по
,
получим
.
Значит,
.
Задачи второго
типа. Задан закон распределения
свободных зарядов
.
Найти закон изменения потенциала в
пространстве
.
Эти задачи обратны по отношению к предыдущим. Здесь нужно интегрировать функцию потенциала.
Пример. В пространстве между обкладками плоского
конденсатора
(рис. 2.12) распределен объемный заряд
с плотностью
,
где
.
Требуется определить закон изменения потенциала в пространстве между электродами .
Полагаем, что размеры электродов намного больше расстояния между ними (для того, чтобы не учитывать краевые эффекты).
Поскольку по осям
y и z изменения Рис. 2.12
заряда нет, то нет изменения потенциала по этим осям.
Следовательно,
.
Дважды проинтегрировав, получим
;
.
Постоянные интегрирования определяем из граничных условий.
При х=0:
,
отсюда
.
При х=2 см: 
;
;
отсюда
.
Таким образом,
.
Задачи третьего типа. Известны потенциалы (или полные заряды) и геометрия тел, создающих поле. Требуется определить закон изменения напряженности или потенциала в пространстве.
П
32
ример. Две металлические пластинки бесконечной протяженности находятся в воздухе, образуя, не соприкасаясь, двугранный угол
(рис. 2.13).
В
.
Определить поверхностный заряд.
Считаем, что
,
тогда
.
Рис. 2.13
Задачу проще решать в цилиндрической системе координат. Поскольку в пространстве, ограниченном гранями угла , нет зарядов, то нужно воспользоваться уравнением Лапласа (в цилиндрической системе координат)
.
Благодаря симметрии потенциал не зависит от высоты (координаты z) и радиуса,
поэтому
,
тогда
.
По условию, при
:
;
при
:
,
;
.
Таким образом,
,
то есть не зависит от r
и z.
Известно,
что
.
П
16
оскольку потенциал зависит только от
,
т. е.
,
то в предыдущем выражении
имеем
,
поэтому напряженность имеет слагаемую только по координате :
.
Из граничных условий («проводник – диэлектрик») имеем
,
.
2.6 Метод зеркальных изображений при решении задач электростатики
Если электрические заряды расположены вблизи границы двух разнородных сред, то расчет поля можно вести, применив искусственный метод, который носит название метода зеркальных изображений.
Идея метода заключается в том, что вместо полупространств неоднородной среды (рис. 2.14) рассматривается полностью однородная среда, влияние же неоднородности на границе раздела сред учитывается введением фиктивных зарядов (рис. 2.15) с учетом граничных условий.
Пример. Заряд q расположен в диэлектрике с проницаемостью на расстоянии h от проводящей плоскости.
Рис. 2.14 Рис. 2.15
Заряд
определяется из граничных условий. Как
видно из рис. 2.15, в области 1 заряд и
среда такие же, как в основной задаче.
Если сейчас во второй задаче граничные
условия будут выдержаны, то векторы
поля в области 1 для обеих задач будут
одинаковы.
На плоскости xoy (рис. 2.16) напряженность поля двух точечных зарядов определяется по формуле
.
На границе раздела
«проводник – диэлектрик» касательная
составляющая
,
поэтому
.
А так как
,
то отсюда
.
Для того чтобы рассчитать поле точечного заряда, расположенного над проводящей средой, фиктивный заряд надо выбирать равным по величине и противоположным по знаку.
Рис. 2.16
Найдем плотность
индуцированных на поверхности зарядов,
исходя из
;
На границе раздела «проводник – диэлектрик»:
А
14
налогично рассчитывается поле заряженной оси, расположенной вблизи проводящей поверхности, например, земли.