2.3. Уравнения пуассона и лапласа
Эти уравнения являются основными дифференциальными уравнениями электростатики. Они вытекают из теоремы Гаусса в дифференциальной форме (2.11).
Чтобы вывести эти уравнения, решим совместно следующую систему:
(2.11)
(2.12)
Подставив (2.12) в (2.11), получим
. (2.13)
Учитывая,
что
,
приходим к следующему выражению:
.
Д
25
ивергенция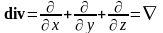
(оператор Гамильтона), тогда окончательно
24
получим
,
или 
.
Эта
формула и есть уравнение
Пуассона. В
тех точках, где нет заряда
—
уравнение Лапласа.
Выражение для
оператора
,
называемого лапласианом, в декартовой
системе координат можно привести к
следующей форме:
Уравнение Пуассона дает связь между частными производными второго порядка от потенциала в любой точке поля и объемной плотностью свободных зарядов в данной точке.
Проводники в электростатическом поле
Если
проводнику сообщить заряд, то под
действием сил отталкивания элементы
этого заряда будут перемещаться по
проводнику и сосредотачиваться на его
поверхности в слое, который можно считать
бесконечно тонким. Внутри проводника
поле существовать не может, поскольку
при возникновении разности потенциалов
(значит
)
возникло бы упорядоченное движение
зарядов, что для электростатики
недопустимо. Все точки проводника, таким
образом, должны иметь один и тот же
потенциал, а это значит, что поверхность
проводника представляет собой
эквипотенциальную
поверхность:
.
Е
22
сли
металлический проводник внести в
электростатическое поле, то под его
действием свободные электроны начнут
перемещаться по проводнику. На одной
части поверхности, обращенной в сторону
более высокого потенциала, сосредотачиваются
отрицательные заряды, а на
противоположной – положительные; к тому же так, что Рис. 2.7
напряженность
внутри проводника станет равной нулю
(рис. 2.7). Поверхность проводника будет
границей электростатического поля,
которое локализовано в диэлектрике,
окружающем проводник.
2.4. Граничные условия в электростатическом поле
Под граничными понимают условия, которым подчиняется поле на границе раздела сред с разными электрическими свойствами.
Р
ассмотрим
границу двух непроводящих сред,
диэлектрическая проницаемость которых
и
.
Пусть на
границе
этих сред имеется поверхностный заряд
св.
(рис. 2.8). Проведем замкнутую
цилиндрическую поверхность так, чтобы
одна ее половина была в первом диэлектрике,
а другая — во втором.
По теореме Гаусса
,
(считаем, что в диэлектрике нет свободных зарядов).
Рис. 2.8
Поток вектора можно представить в виде суммы четырех потоков
.
Если площадка
невелика
,
то можно считать, что во всех точках
этой площадки вектор
имеет одну и ту же величину (рис. 2.9,а).
Тогда скалярное произведение векторов
для площади
1
запишется
.
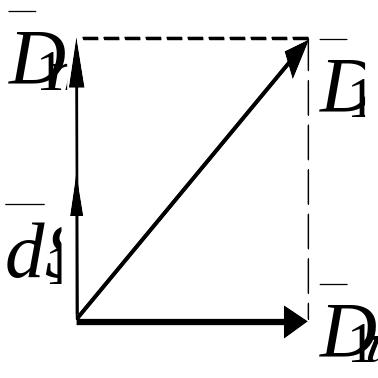Рис. 2.9,а Аналогично имеем
,
знак
«-» из-за того, что угол между векторами
отличается от первого случая на 1800
(рис. 2.9,б).
Если
высоту цилиндра уменьшить, то в пределе,
когда
и
сольются с
,
два последних интеграла в сумме
.
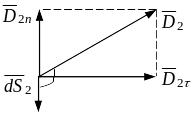Тогда
или
.
Рис. 2.9,б Нормальная составляющая вектора электрического смещения на границе раздела двух непроводящих сред претерпевает скачок, равный поверхностной плотности заряда.
Частные случаи.
1. На
границе нет свободных
зарядов:
св.=0.
Тогда
.
2
; 
; (знак определяется направле-
ниями
и
). Рис. 2.10
На границе раздела «диэлектрик – проводник» поверхностная плотность свободных зарядов численно равна нормальной составляющей вектора в диэлектрике у границы раздела.
Д
алее
получим граничное условие для
тангенциальных составляющих вектора
.
Проведем замкнутую линию l
так, чтобы одна ее часть была в первом
диэлектрике, другая – во втором
(рис. 2.11).
Зададимся направлением обхода по контуру 1-2-3-4 по часовой стрелке. В электростатическом поле циркуляция равна нулю:
,
если
,
то вектор
на
,
Поэтому
Если отрезки
и
уменьшить так, Рис. 2.11
чтобы
и
совпали с
на граничной поверхности, то
,
поэтому 
.
Отсюда получим
новое граничное условие:
.
На границе двух непроводящих сред тангенциальные составляющие вектора напряженности электрического поля равны.
О
29
тметим, что на поверхности раздела сред потенциал непрерывен, т.е.
.