Напряжение, потенциал и разность потенциалов в электростатическом поле
Напряжением между двумя точками электростатического поля называется работа сил поля по перемещению единичного заряда из одной точки поля в другую:
,
причем эта работа не зависит от того, по какому пути перемещается заряд.
Потенциалом
в электростатике называется некоторая
скалярная функция
,
отрицательный градиент которой равен
вектору напряженности (рис. 2.2).
. (2.4)
Рис. 2.2
Градиент потенциала в декартовой системе записывается:
;
;
; 
; 
.
Если взять произвольное направление на координате l (рис. 2.3), то
;
знак
«-» говорит о том, что вектор
направлен в сторону уменьшения потенциала
.
Из последнего выражения получим
. (2.5)
Рис. 2.3 Выражение (2.5) является интегральной формой уравнения (2.4) и определяется с точностью до постоянной интегрирования.
И
20
з выражения (2.5) следует, что подынтегральная величина численно равна работе сил поля по перемещению единичного положительного заряда на расстояние
.
Т
28
аким образом, понятию потенциала можно придать физический смысл.Потенциал точки электростатического поля численно равен работе, которую могут совершить силы поля при перемещении единичного положительного заряда из данной точки поля в точку с нулевым потенциалом.
Из определения потенциала следует, что потенциал одной и той же точки может быть различным, в зависимости от того, где выбрана точка с нулевым потенциалом.
Чаще
всего нулевой потенциал принимается
в бесконечно удаленной точке. Тогда
,
если
.
Разность потенциалов между двумя точками электростатического поля при условии запишется
.
Для электростатического поля понятие разности потенциалов и напряжения совпадают.
Пример. Поле точечного заряда (рис. 2.4). Определить потенциал точки А при известном заряде q и расстоянии rА до этой точки.
Из теоремы Гаусса с учетом сферической симметрии поля имеем:
;
,
.
21
Рис. 2.4
;
.
Вывод. Величина напряженности электрического поля снижается по квадратичной зависимости, а потенциал — обратно пропорционально расстоянию от центра заряда до рассматриваемой точки.
2.2 Теорема гаусса в интегральной форме при расчете электростатических полей
Теорема Гаусса является одной из фундаментальных теорем электростатики. Она гласит:
Поток
вектора электрического смещения
сквозь замкнутую поверхность S
равен алгебраической сумме свободных
зарядов
,
находящихся внутри объема, ограниченного
данной поверхностью.
— интегральная форма.
Теорему Гаусса в интегральной форме удобно использовать для определения или заряженных симметричных тел. В этом случае удается провести замкнутую поверхность так, чтобы все точки этой поверхности оказались в одинаковых условиях по отношению к заряду, находящемуся в замкнутой поверхности. Часто такими поверхностями являются цилиндр, сфера, плоскость.
Пример 1. Поле заряженной оси (рис. 2.5).
;
электрическое поле имеет симметричную
форму — цилиндрическую.
.
В случае однородной и изотропной среды
(2.6)
Рис. 2.5
; (2.7)
. (2.8)
Подставив (2.7) и (2.8) в (2.6), получим
;
; (2.9)
. (2.10)
П
S
ример 2. Известна поверхностная плотность заряда
Кл/м2
на поверхности зем-ного шара. Нижние
слои атмосферы заря-жены положительными
зарядами с объемной плотностью заряда
Кл/м3
(усредненное значение).
Рассчитать значение и направление
вектора напряженности электрического
поля на высоте h=1000 м
над поверхностью земли. Принять радиус
земли R
равным 6000 км.
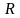Рис. 2.6
Решение выполним на основе теоремы Гаусса.
1. Окружим земной шар и часть атмосферы сферической поверхностью, радиус которой равен R+h (на рис. 2.6 S показана штрихами) и используем интегральное выражение теоремы Гаусса:
.
В силу сферической
симметрии электрического поля, в любой
точке сферы Е=const
и направление совпадает с направлением
элемента
.
2. Тогда левая часть будет равна:
.
3. Заряд, находящийся внутри сферической поверхности:
Ввиду большой величины радиуса земного шара R по сравнению с h можно определить объем нижних слоев атмосферы более просто:
.
Тогда положительный заряд
,
а весь заряд внутри поверхности S
.
4. В результате получим:
,
В/м
Знак «минус» означает, что напряженность электрического поля направлена вниз к земному шару в любой точке поверхности S (противоположно внешней нормали).
Легко рассчитать, что на поверхности земли:
В/м,
а
на высоте
м
напряженность электрического поля Е0 равна 0.