
- •Теоретические основы электротехники Электромагнитное поле
- •Рецензенты:
- •Учебное издание
- •Теоретические основы электротехники Электромагнитное поле
- •428015 Чебоксары, Московский просп., 15 Введение
- •Глава 1. Общие сведения
- •Основные векторы электромагнитного поля и макроскопические параметры
- •Вектор напряженности электрического поля .
- •2. Вектор электрического смещения .
- •4. Вектор электрической поляризации .
- •5. Вектор намагниченности .
- •6. Вектор магнитной индукции .
- •1.2. Система уравнений максвелла для электромагнитного поля
- •Первое уравнение максвелла
- •Физический смысл первого уравнения Максвелла.
- •Непрерывность токов проводимости и токов смещения
- •Второе уравнение максвелла
- •Третье уравнение максвелла
- •Четвертое уравнение максвелла
- •Полная система уравнений максвелла
- •Теорема о единственности решений системы уравнений максвелла
- •Глава 2. Электростатическое поле
- •2.1 Основные понятия и определения
- •Напряжение, потенциал и разность потенциалов в электростатическом поле
- •2.2 Теорема гаусса в интегральной форме при расчете электростатических полей
- •2.3. Уравнения пуассона и лапласа
- •Проводники в электростатическом поле
- •2.4. Граничные условия в электростатическом поле
- •2.5. Задачи электростатики
- •2.6 Метод зеркальных изображений при решении задач электростатики
- •Глава 3.Емкость. Примеры расчета емкостей
- •3.1. Емкость плоского конденсатора
- •3.2. Емкость двухслойного плоского конденсатора
- •3.6. Поле и емкость двухпроводной линии
- •3.7. Емкость системы несоосных проводов
- •3.8. Емкость системы «провод-земля»
- •3.9. Поле двух заряженных проводов, находящихся над поверхностью земли
- •Глава 4. Энергия и силы электростатического поля
- •4.1. Энергия взаимодействия точечных зарядов
- •4.2. Энергия электростатического поля
- •4.3. Силы, действующие в электрическом поле
- •Глава 5.Электрическое поле постоянного тока в проводящей среде
- •5.1. Основные законы
- •Закон ома в дифференциальной форме
- •Первый закон кирхгофа в диффеннциальной форме
- •Рассмотрим иной вариант доказательства.
- •Закон джоуля-ленца в дифференциальной форме
- •5.2. Поле полусферического электрода
- •5.3.Граничные условия в электростационарном поле
- •5.4. Аналогия между электрическим полем постоянного тока и электростатическим полем
- •Глава 6.Магнитное поле, постоянное во времени.
- •6.1. Основные понятия и законы
- •Вектор напряженности магнитного поля
- •З аконы ампера и био — савара
- •Магнитный поток и его непрерывность
- •Закон полного тока для стационарного магнитного поля
- •6.2. Граничные условия в магнитном поле
- •Закон преломления вектора
- •6.3 Векторный потенциал магнитного поля
- •6.4. Скалярный магнитный потенциал
- •6.5. Аналогия между магнитным полем постоянного тока и полем электростатики
- •Связь между магнитным потоком и векторным потенциалом
- •6.6.Энергия и силы магнитного поля.
- •6.7. Индуктивность
- •6.8. Взаимоиндуктивность
- •6.9. Методы расчета магнитных полей
- •Метод зеркальных изображений для расчета магнитного поля
- •7.1. Полный электрический ток и его непрерывность
- •Непрерывность полного тока
- •7.2. Уравнения максвелла в комплексной форме
- •7.3.Теорема умова — пойнтинга
- •- Теорема Умова — Пойнтинга.
- •7.4. Теорема умова — пойнтинга в комплексной форме
- •Глава 8. Плоские электромагнитные волны
- •8.1. Уравнения плоской волны
- •8.2. Свойства плоских волн
- •Выводы:
- •8.3. Распространение плоской электромагнитной волныв проводящей среде
- •8.4. Поверхностный эффект
- •8.5. Экранирование в переменном электромагнитном поле
- •8.6. Распространение плоской электромагнитной волны в идеальном диэлектрике
- •Глава 9. Векторы и потенциалы переменного электромагнитного поля
- •9.1. Уравнения для векторов переменного эмп
- •9.2. Потенциалы переменного эмп
- •9.3. Уравнения для электродинамического потенциала
- •9.4. Запаздывающие и опережающие потенциалы переменного электромагнитного поля.
- •Комплексная форма записи запаздывающего потенциала
- •Понятие о квазистационарном и квазистатическом полях
- •Список рекомендуемой литературы Основная
- •Дополнительная
- •Оглавление
- •Глава 1. Общие сведения 6
- •Глава 2. Электростатическое поле 18
- •Глава 3. Емкость. Примеры расчета емкостей 35
Четвертое уравнение максвелла
Это уравнение отражает принцип непрерывности магнитных силовых линий. В интегральной форме условие непрерывности линий вектора магнитной индукции записывается в виде
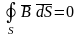 . (1.7)
. (1.7)
Применив его к элементарному объему V и перейдя к пределу, получим в дифференциальной форме:
 . (1.8)
. (1.8)
Физический смысл уравнения (1.8) в том, что отсутствуют истоки вектора магнитной индукции, то есть в природе не существует магнитных зарядов. Силовые линии вектора непрерывны, они либо замкнуты, либо уходят в бесконечность.
Отметим, что интегральная и дифференциальная формы записи уравнений ЭМП (табл. 1.1) дополняют друг друга и позволяют выполнять расчеты полей любой сложности. Различие в том, что интегральная форма описывает соотношения между основными векторами ЭМП в конечной области, а дифференциальная форма выражает характер их изменения непосредственно в каждой точке, для которой она записана.
Таблица 1.1
Интегральная форма |
Дифференциальная форма |
|
|
|
|
|
|
|
|
Полная система уравнений максвелла
Эта
система уравнений, кроме рассмотренных
четырех уравнений, включает также
попарные соотношения между
и
,
и
 ,
и
.
Дополнительно следует учитывать
граничные у
,
и
.
Дополнительно следует учитывать
граничные у
32
словия на плоскости раздела разных сред. Это обусловлено тем, что электротехнические устройства состоят из различных материальных сред (проводники, диэлектрики и т.п.), в связи с чем ЭМП приходится рассчитывать в кусочно-неоднородной среде.Пока без доказательств приведем следующие граничные условия для двух сред 1 и 2:
 ;
;
 ;
;
 ;
;
 ,
,
где
 —-
тангенциальные, n –
нормальные составляющие.
—-
тангенциальные, n –
нормальные составляющие.
Итак, полная система уравнений Максвелла представлена в табл. 1.2:
Таблица 1.2
Основные уравнения |
Дополнительные уравнения |
;
. |
|
где  —
вектор плотности токов проводимости
[А/м2];
—
вектор плотности токов проводимости
[А/м2];
— удельная электрическая проводимость среды [См/м];
— вектор напряженности, вызванной электрическими силами;
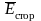 —
вектор
напряженности, вызванной сторонними
(неэлектрическими) силами.
—
вектор
напряженности, вызванной сторонними
(неэлектрическими) силами.
Как указывалось, приведенная система дополняется граничными условиями.
Теорема о единственности решений системы уравнений максвелла
Электромагнитное
поле в любой момент времени
 в любой точке объема, ограниченного
замкнутой поверхностью, однозначно
определяется уравнениями Максвелла,
если для начального момента времени
в любой точке объема, ограниченного
замкнутой поверхностью, однозначно
определяется уравнениями Максвелла,
если для начального момента времени
 известны напряженности электрического
и магнитного полей в любой точке этого
объема, а также заданы тангенциальные
составляющие напряженности электрического
и магнитного полей в каждой точке
поверхности, ограничивающей данный
объем, начиная с момента времени
до любого момента
.
известны напряженности электрического
и магнитного полей в любой точке этого
объема, а также заданы тангенциальные
составляющие напряженности электрического
и магнитного полей в каждой точке
поверхности, ограничивающей данный
объем, начиная с момента времени
до любого момента
.
Глава 2. Электростатическое поле
2.1 Основные понятия и определения
Электрические и магнитные поля неразрывно связаны друг с другом, но часто при расчете полей удобно рассматривать эти стороны единого явления отдельно. Будем различать электростатику и магнитостатику. Вначале рассмотрим электростатические поля.
Источником электростатического поля являются «неподвижные» во времени и пространстве заряды.
Процессы, происходящие
в этом поле, не зависят от времени, а
следовательно все
 .
.
Тогда система уравнений Максвелла для электростатики примет вид
 ; (2.1)
; (2.1)
; (2.2)
.
В интегральной форме выражению (2.1) соответствует уравнение
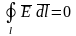 . (2.3)
. (2.3)
Выражения (2.1) и (2.3) имеют тот смысл, что поле электростатики является безвихревым (силовые линии имеют начало и конец).
 —
работа, совершаемая
силами поля по перемещению единичного
заряда из одной точки в другую.
—
работа, совершаемая
силами поля по перемещению единичного
заряда из одной точки в другую.
Смысл уравнения (2.3) еще и в том, что работа сил поля по замкнутому контуру равна нулю (рис. 2.1). Это есть признак потенциальности поля.
Из выражения (2.3) также следует, что работа, совершаемая силами поля, не зависит от формы пути.
 ;
;
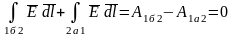


Доказанное
равенство является достаточным Рис. 2.1
и необходимым условием того, что
электростатическое
поле потенциальное и безвихревое:
циркуляция
 и
и
 .
.






 ;
; ;
; ;
; ;
; -
закон Ома в дифференциальной форме,
-
закон Ома в дифференциальной форме,