5. Вектор намагниченности .

Характеризует реакцию ферромагнитного вещества на действие магнитного поля.

В магнитном поле реакция вещества проявляется в появлении дополнительного магнитного момента , создаваемого элементарными токами i (рис. 1.8).

, [Ам²]; , если и , если .

Явление упорядоченной ориентации элементарных токов (или магнитных моментов) при называется намагничиваемостью и характеризуется вектором намагниченности ,

Вектор является мерой среднего магнитного момента единицы объема вещества.

6. Вектор магнитной индукции .

Х арактеризует силовое воздействие на движущийся заряд q (рис. 1.9).

Эта сила называется силой Лоренца и

Рис. 1.9 определяется по формуле: ,

где  — вектор скорости движения заряженной частицы;

 — сила, воздействующая на заряд;

 — индукция, [Тл].

Численно магнитная индукция , Тл.

Вектор магнитной индукции имеет направление, перпендикулярное к векторам силы и скорости. При этом сила получается наибольшей.

7. Вектор напряженности магнитного поля .

Из этого соотношения следует, что .

Для ряда полей справедливо , где k – безразмерный коэффициент, называемый магнитной восприимчивостью вещества.

Для линейной среды

,

где  — относительная магнитная проницаемость (безразмерная величина);

10

 — магнитная постоянная.

1.2. Система уравнений максвелла для электромагнитного поля

Расчет пространственного распределения ЭМП в простейших симметричных системах может производиться с помощью интегральных законов. К решению задач для сложных систем уравнения в интегральной форме неприменимы, так как под знаком интеграла содержатся неизвестные значения величин для различных точек пространства. Поэтому эти уравнения приводятся к дифференциальной форме.

Первое уравнение максвелла

В интегральной форме закон полного тока записывается в виде

.

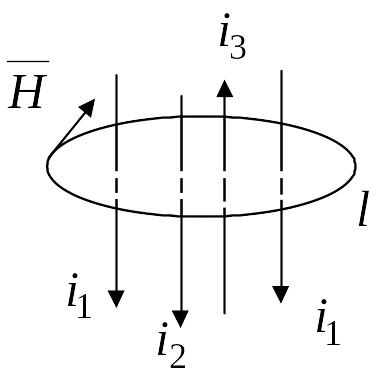Циркуляция вектора по замкнутому контуру l равна сумме токов, пронизывающих поверхность, ограниченную данным контуром (рис. 1.10).

Рис. 1.10

Направления вектора напряженности и тока проводимости связаны правилом правоходового винта

.

Английский ученый Максвелл, развивая теорию ЭМП, кроме токов проводимости ввел для пустоты понятие токов смещения с плотностью

.

С учетом токов смещения, закон полного тока преобразуется и будет иметь следующий вид

11

. (1.1)

Можно перейти к дифференциальной форме записи этого интегрального уравнения, используя теорему Стокса

.

Учитывая, что это равенство справедливо при любых поверхностях, можно записать

(1.2)

Выражение (1.2) — это дифференциальная форма записи первого уравнения Максвелла.

Н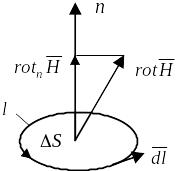 апомним, что ротор (вихрь) – вектор, характеризующий интенсивность вихревых полей в каждой точке (рис. 1.11). Проекция этого вектора определяется выражением

,

где n — нормаль, определяемая правилом

Рис. 1.11 правоходового винта;

 — площадь, ограниченная контуром интегрирования l.

Физический смысл первого уравнения Максвелла.

П

12

олученное выше векторное выражение (1.2) означает, что источником магнитного поля являются токи проводимости, а также переменное во времени электрическое поле. Причем характер магнитного поля, вызываемого этими двумя факторами, носит идентичный вихревой характер (рис. 1.12).

для проводящей среды среды

для диэлектрической среды среды

Рис. 1.12

36