8.2. Свойства плоских волн

Пусть .

Эквифазные плоскости этой волны представляют собой

плоскости, перпендикулярные оси z. Скорость движения волны

называется фазовой скоростью.

В момент в точке фаза волны равна

,

а в момент волна имеет фазу

.

Приравнивая эти выражения, получим

;

.

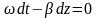Фазовая скорость падающей волны такая же. Отраженные волны перемещается с такой же фазовой скоростью, но в обратном направлении: .

Коэффициент распространения определяет затухание (  — коэффициент ослабления или затухания) и скорость распространения волны (  — коэффициент фазы).

Отметим, что отношение амплитуд и называется волновым сопротивлением

,

т. е. отношение

,

а векторы и сдвинуты по фазе на .

Если фаза распространения не ограничена, то отраженных

волн нет, а постоянная обратится в нуль.

Определим длину волны.

Длиной волны называют расстояние, на котором фаза волны изменяется на .

Пусть .

Тогда

.

Отсюда ; .

Так как ,

то .

Покажем картину поля (рис. 8.4) при отсутствии потерь, то есть при . Тогда , , 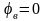т. е. фазы и равны нулю.

Рис. 8.4

Расстояние вдоль направления распределения волны (вдоль оси z), на котором амплитуда падающей волны уменьшится в е раз, называется глубиной проникновения волны .

,

где .

Выводы:

1. В каждой точке поля мгновенное значение напряженности электрического поля равно сумме падающей и отраженной волн, а мгновенное значение напряженности магнитного поля равно разности падающей и отраженной волн.

2. Направление вектора , одинаковое во всех точках поля, перпендикулярно направлению вектора , причем оба вектора перпендикулярны направлению распространения.

3. Отношение амплитуд и , так же как и отношение и , равно модулю волнового сопротивления, т. е.

.

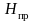4. Фазы падающих волн и , так же как и фазы отраженных волн, сдвинуты одна относительно другой на угол, равный аргументу волнового сопротивления .

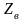5. Падающая и отраженная волна распространяются с одинаковой скоростью в прямо противоположных направлениях.

6. Амплитуды волн затухают в направлении своего распространения. Быстрота затухания зависит от коэффициента затухания .

7. Если среда не ограничена в направлении распространения, то отраженных волн нет:

; .

8.3. Распространение плоской электромагнитной волныв проводящей среде

Рассмотрим однородную проводящую среду, простирающуюся в бесконечность. Следовательно, падающая волна не встречает границы, которая изменила бы распространение, и отраженной волны не возникает.

; .

Так как в этом случае 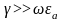, то током смещения можно пренебречь.

Коэффициент распространения:

,

где 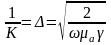 — глубина проникновения.

Таким образом , а волновое сопротивление:

.

Фазовая скорость .

Длина волны .

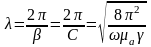Поскольку имеется только падающая волна, то при условии

;

.

Амплитуды векторов поля убывают в направлении распространения, что обусловлено поглощением энергии средой (рис. 8.5).

Рис. 8.5

Так как 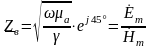, то волны E и Н сдвинуты по фазе на . На расстоянии, равном длине волны , векторы поля практически обращаются в нуль:

.