7.4. Теорема умова — пойнтинга в комплексной форме

Поскольку вектор Пойнтинга через замкнутую поверхность S характеризует мощность, доставляемую внутрь объема V, ограниченного этой поверхностью, то по аналогии с мощностью цепи переменного тока рассмотрим комплексный вектор Пойнтинга:

,

так как .

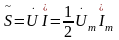Рассмотрим поток комплексного вектора Пойнтинга:

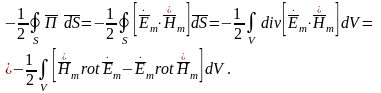(7.5)

Воспользуемся уравнениями Максвелла в комплексной форме:

которые могут быть преобразованы к виду:

Подставив последние выражения в (14.3) , получим

,

где

 — активная мощность Р;

 — разность магнитной и электрической мощностей (реактивная мощность).

Перейдя к действующим значениям, можно записать:

Поток комплексного вектора Пойнтинга, входящий внутрь некоторого объема сквозь его граничную поверхность, равен всей комплексной мощности, поступающей извне в этот объем.

В таком виде теорема Умова — Пойнтинга часто используется для определения активного и внутреннего реактивного сопротивлений проводников на переменном токе.

Глава 8. Плоские электромагнитные волны

Источником электромагнитных волн являются изменяющиеся во времени токи и заряды. Всякая электрическая цепь переменного тока может излучать электромагнитные волны, несущие с собой определенную энергию, зависящую от амплитуды и частоты тока, от конфигурации цепи и от свойств диэлектрика, окружающего излучающую цепь.

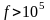Для промышленной частоты  Гц эта излучаемая мощность пренебрежимо мала. Мощность излучения учитывают при  Гц.

Установлено, что обычно поле имеет волновой характер.

Плоской электромагнитной волной называется волна, у которой поверхность равных фаз представляет собой плоскость (рис. 8.1).

П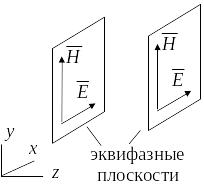 лоская волна называется однородной, если векторы поля и при соответствующем выборе направления осей координат зависят от одной пространственной координаты и времени. Отсюда следует, что во всех точках эквифазной плоскости модули и одинаковы.

Нас будут интересовать прежде всего синусоидальные волны. Они называются гармоническими или монохроматическими.

Р

Рис. 8.1

ассмотрим распространение однородной линейно-поляризованной монохроматической волны:

;

;

.

8.1. Уравнения плоской волны

Пусть среда однородна, а вектор напряженности электрического поля имеет одну проекцию , которая зависит только от одной пространственной координаты z и от времени t.

Параметры среды , и постоянные. Найдем уравнение волны.

По второму уравнению Максвелла

.

Поскольку , и все частные производные, кроме , равны 0, то

;

Следовательно, напряженность магнитного поля имеет лишь составляющую

.

Поскольку зависит только от z, то частные производные можно заменить на обычные:

(8.1)

Первое уравнение Максвелла:

примет вид

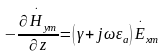
или

(8.2)

Подставим в (14.2) уравнение (14.1):

Получим дифференциальное уравнение:

. (8.3)

Коэффициент

называется коэффициентом распространения,

 – коэффициент ослабления (затухания),

 — коэффициент фазы.

Тогда уравнение (8.3) упростится

.

Поскольку волна распространяется только вдоль одной координаты, то отбросив индексы у проекций векторов, получим решение

.

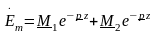Перейдем к мгновенным значениям. Учтем, что

;

.

Первая составляющая называется падающей, а вторая – отраженной волной; и  — начальные фазы волн. Мгновенное значение волны равно сумме ординат падающей и отраженной волн.

Падающая волна движется в сторону увеличения координаты z, причем с увеличением z ее величина падает со скоростью уменьшения экспоненты , отраженная — наоборот (рис. 8.2).

Рис. 8.2

Напряженность магнитного поля:

.

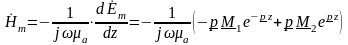Комплексную величину

называют волновым сопротивлением [Ом].

Тогда

.

Мгновенные значения (с учетом )

Мгновенное значение вектора Пойнтинга (рис. 8.3)

.

Рис. 8.3

Знак «-» при характеризует то, что направление вектора Пойнтинга совпадает с направлением распространения отраженной волны.