Непрерывность полного тока

Докажем, что полный ток непрерывен, поэтому дивергенция плотности полного тока всегда равна нулю.

Плотность полного тока состоит из суммы плотностей токов проводимости и смещения:

.

Тогда .

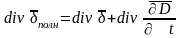Поскольку ,

а x, y и z не зависят от t, то дивергенция тока смещения:

,

так как по теореме Гаусса . Из уравнения непрерывности тока проводимости для (7.4):

 — закон сохранения заряда.

Отсюда ,

что и требовалось доказать.

Плотность полного тока представляет собой соленоидальный вектор, не имеющий ни источников, ни стоков.

П ример. Конденсатор, заряженный, разряжается на резистор (рис. 7.5).

Линии тока проводимости непрерывно переходят в линии тока поляризации.

Р

104

ис. 7.5

7.2. Уравнения максвелла в комплексной форме

Электромагнитное поле определяется четырьмя векторами: , , , . Для сред с , 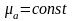имеем 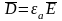, , поэтому при расчете достаточно определить только два вектора: и . Их обычно определяют из уравнений Максвелла. Однако для однозначности определения и этих уравнений недостаточно, поскольку и не определяют однозначно векторы и . Поэтому задают еще два уравнения, определяющие дивергенции этих векторов.

Предположим, что проекции векторов поля и изменяются во времени по синусоидальному закону, причем фазы всех трех прямоугольных проекций равны. Такая электромагнитная волна называется линейно — поляризованной.

;

;

.

Введем в рассмотрение комплексную амплитуду:

.

Тогда мгновенное значение:

.

Аналогично можно определить и комплексную амплитуду .

Уравнения Максвелла справедливы и для комплексных векторов, поскольку они справедливы отдельно и для действительной, и для мнимой части комплексных векторов и .

Подставим комплексные амплитуды в уравнения.

Например, первое уравнение Максвелла запишется в виде:

.

После сокращения имеем:

.

Аналогично получаем:

;

;

.

Удобство комплексной формы заключается в том, что время исключается из уравнений Максвелла.

7.3.Теорема умова — пойнтинга

Эта теорема выражает закон сохранения энергии в электромагнитном поле.

Энергия электромагнитного поля в объеме V:

. (7.3)

Энергия электромагнитного поля непрерывно меняется во времени:

. (7.4)

Из первого уравнения Максвелла:

.

Из второго уравнения Максвелла:

.

Подставим эти выражения в уравнение (7.4):

.

Известно, что , следовательно,

.

Вектор называется вектором Пойнтинга, его величина выражается в ВА/м².

Поскольку (по теореме Остроградского)

,

то мощность в единицу времени, доставляемая внутрь некоторого объема, ограниченного S, запишется:

- Теорема Умова — Пойнтинга.

Поток вектора Пойнтинга, входящий в замкнутую поверхность S, равен сумме двух мощностей, одна из которых является мощностью тепловых потерь внутри объема V, ограниченного поверхностью S, другая

соответствует изменению энергии электромагнитного поля в том же объеме.

М ощность всегда положительна. Мощность , соответствующая изменению электромагнитной энергии, может быть и положительной и отрицательной. Если она

п

Рис. 7.6

оложительна, то электромагнитная энергия внутри объема V увеличивается. В этом случае поток вектора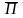 , входящий в поверхность S, будет положительным. Поскольку положительная нормаль к поверхности 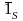направлена в наружную сторону, то так же направлен вектор 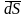(рис. 7.6). Поэтому для того, чтобы поток вектора был положительным, вектор преимущественно должен быть направлен внутрь объема V (угол между и преимущественно должен быть тупым).

При выводе теоремы мы предполагали, что внутри объема V, замкнутого поверхностью S, нет источников энергии. Если в V есть источник мощностью , то теорема должна учитывать это:

,

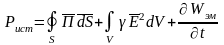где  — мощность энергии, выходящей через граничную поверхность S объема V;

 — мощность тепловых потерь;

 — мощность изменения энергии электромагнитного поля в объеме V.

Таким образом, теорема Умова — Пойнтинга связывает изменение энергии электромагнитного поля в каком-либо объеме V с потоком через поверхность, ограничивающей этот объем

Если , то получается активный баланс (рис. 7.7) (преобладает отдача энергии во внешнее пространство).

Рис. 7.7

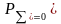 — нейтральный баланс (рис. 7.8).

поток энергии проходит насквозь (входящие и выходящие векторы равны)

вектор не входит в область V

Рис. 7.8

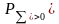 — пассивный баланс (рис. 7.9).

Рис. 7.9

 — преобладает поглощение энергии над излучением.

Пример 1. Определить поток энергии, проходящей через поверхность бесконечного цилиндрического провода с постоянным током I (рис. 7.10).

Р

Рис. 7.10

анее доказано, что .

.

На поверхности провода векторы и взаимно перпендикулярны. Поэтому ;

.

Вектор направлен внутрь провода, исходя из направлений и .

;

,

где  — электрическое сопротивление данного участка.

Провода потребляют энергию из диэлектрика на покрытие тепловых потерь. Входящий поток энергии равен мощности, поглощаемой согласно закону Джоуля — Ленца.

Пример 2. Передача энергии двухпроводной линией (рис. 7.11).

110

Рис. 7.11

В любой точке поля направлен одинаково. Передача энергии от источника к нагрузке осуществляется ЭМП, распространяющимся в диэлектрике между проводами. Роль проводов в том, что заряды, распределенные на их поверхности, создают электрическое поле 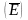, а протекающие по ним токи – магнитное поле . Эти поля обладают наибольшей интенсивностью в пространстве между проводами, в котором передается основная часть энергии.

Пример 3. Передача энергии по коаксиальному кабелю (рис. 7.12).

Рис. 7.12

Примем проводимость диэлектрика .

По закону полного тока напряженность магнитного поля в диэлектрике: .

Напряженность электрического поля в диэлектрике:

,

так как ,

где  — линейный заряд жилы;

U – напряжение между жилой и оболочкой.

В точке диэлектрика, расположенной в области , получим

.

Поток вектора через кольцо с и :

.

Вся энергия передается по диэлектрику. Если , то часть энергии затрачивается на нагрев.