6.9. Методы расчета магнитных полей

Расчет магнитного поля чаще всего сводится к определению вектора напряженности . В тех случаях, когда трудно определить из-за больших математических выкладок, удобно ввести векторный потенциал , а затем определить как .

При расчете магнитных полей в основном используются:

а) метод наложения (пример расчета магнитного поля двухпроводной линии);

б) применение закона полного тока в интегральной форме (пример расчета магнитного поля уединенного проводника);

в) применение первого уравнения Максвелла;

г) интегрирование уравнения Пуассона или Лапласа для векторного потенциала;

д) метод зеркальных изображений

и ряд других методов.

Пример 1. (Применение первого уравнения Максвелла). Исследовать магнитное поле трубчатого проводника с постоянным током I (рис. 6.35).

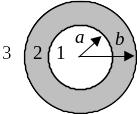
Область, занятая полем, делится на три части:

1)  ;

2)  ;

3

Рис. 6.35

)  ;

Ось z цилиндрической системы направим вдоль проводника (рис 6.36). Тогда в силу симметрии вектор будет иметь лишь одну проекцию , которая будет изменяться в зависимости от r.

1) Определим .

;

;

;

Рис. 6.36

;

.

Определим . Надо иметь в виду, что  — величина конечная (поскольку энергия магнитного поля конечная). Тогда , поскольку иначе при имели бы . Это значит, что и , а, следовательно, в области 1 поля нет.

2) Определим .

;

,

тогда .

Заменим переменные: .

Тогда ; .

В итоге:

; .

Интегрируем:

;

отсюда ; ;

; ;

.

Определим . Для этого учтем, что на границе должно иметь место равенство , поскольку на границе нет поверхностных токов, а .

Тогда ,

и ,

откуда .

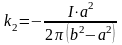Напряженность поля:

.

3 )  (аналогично случаю 1).

При имеем ;

; .

Тогда .

Зависимость Н(r) приведена на рис. 6.37.

Если по сплошному цилиндрическому проводу радиусом b протекал бы ток I, то поле в области было бы таким же, что и в случае трубчатого проводника.

Метод зеркальных изображений для расчета магнитного поля

Случай 1. Магнитные проницаемости и соизмеримы.

Согласно метода зеркальных изображений исходная схема приводится к расчетной, как показано на рис. 6.38.

Исходная схема Расчетные схемы

Рис. 6.38

Используя граничные условия, получим:

а)  ;

;

; (6.11)

б)  ;

;

. (6.12)

Из (6.11) и (6.12):

Напомним, что для электростатики:

;

.

Случай 2. Проводник находится над поверхностью с (рис. 6.39).

Рис. 6.39

Здесь имеет место зеркальное отображение, но без перемены знака тока (в отличие от аналогичного случая в электростатическом поле). Значение Н в любой точке среды с может быть найдено с применением метода наложения и закона полного тока.

Г

99

ЛАВА 7. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ

Как указывалось ранее, под электромагнитным полем понимают совокупность взаимосвязанных и обусловливающих друг друга электрического и магнитного полей. Магнитное поле всегда является следствием электрического тока.

7.1. Полный электрический ток и его непрерывность

1. Электрический ток в проводящей среде представляет собой упорядоченное движение электрических зарядов под действием сил поля. Такой ток называют током проводимости. Он подчиняется закону Ома:

.

2. Если заряженные тела или частицы движутся в непроводящей среде или вакууме со скоростью , то они образуют токи переноса. Плотность тока переноса:

,

где  — объемная плотность заряда.

3. В молекулах диэлектрика, который вносится в электрическое поле, под действием сил поля связанные заряды будут перемещаться и образуют ток поляризации. Плотность тока поляризации пропорциональна быстроте изменения вектора поляризации:

.

Для сред, в которых поляризованность пропорциональна напряженности поля , имеем:

.

4. При изменении электрического поля в вакууме образуется магнитное поле. Максвелл предложил назвать такое изменение электрического поля током смещения в вакууме:

.

Ток смещения отличается от других токов тем, что он не вызывает тепловых потерь.

Ток проводимости и ток переноса могут иметь место и в постоянных, и в переменных во времени электрических полях. Ток поляризации и ток смещения в вакууме имеют место только в переменных во времени электрических полях.

Таким образом, электрическим током называют два физически разнородных явления – движение электрических зарядов и изменение электрического поля во времени. Поэтому полным током называют совокупность всех явлений, при которых образуется магнитное поле.

В общем случае плотность полного тока равна сумме:

.

Сумму называют током смещения в диэлектрике или просто током смещения. Плотность тока смещения в диэлектрике равна:

.

Отсюда следует, что току смещения присуще свойство распространяться в диэлектрике, так же как и току проводимости в проводнике.

Сходство между токами проводимости и токами смещения только в том, что они одинаковым образом вызывают магнитное поле (рис. 7.1), а физическая сущность их отлична.

Токи проводимости соответствуют движению зарядов, а токи смещения – лишь изменению во времени вектора напряженности электрического поля.

Рис. 7.1

Непрерывность токов проводимости и токов смещения:

;

;

.

Последнее выражение говорит о том, что там, где кончаются линии токов проводимости, начинаются линии токов смещения и наоборот.

В дальнейшем не будем рассматривать ток переноса. Поэтому под полным током следует понимать:

.

Как видим, полный ток может возникать и в проводящей, и в непроводящей среде. В хорошо проводящей среде преобладает ток проводимости, причем значительно, поэтому в таких средах током смещения пренебрегают.

В диэлектрике с малыми потерями дело обстоит наоборот, там ток смещения велик по сравнению с токами проводимости.

В полупроводниках токи проводимости и токи смещения соизмеримы и должны учитываться оба.

Предположение Максвелла о том, что в диэлектриках возбуждаются токи смещения подобно тому, как в проводниках – ток проводимости, объясняет тот факт, что электрические устройства могут излучать в окружающее пространство энергию, которая распространяется в диэлектрике вместе с электромагнитными волнами.

УРАВНЕНИЕ НЕПРЕРЫВНОСТИ ТОКА ПРОВОДИМОСТИ

Л

Рис. 7.2

инии вектора плотности тока непрерывны, поэтому постоянные токи могут быть только в замкнутых цепях: в проводниках . Постоянный ток через произвольную замкнутую поверхность (рис. 7.2) должен быть всегда равен нулю. Величина заряда в объеме V, ограниченном такой поверхностью S, всегда постоянен и неизменен во времени.

П

Рис. 7.3

Рис. 7.4

еременные токи проводимости могут иметь место и в незамкнутых проводниками цепях, например, цепь с конденсатором (рис. 7.3). Следовательно, в переменных полях цепи с токами проводимости могут быть незамкнутыми. Там, где заканчиваются линии токов проводимости, могут накапливаться заряды. Поэтому поток вектора плотности тока через замкнутую поверхность может не равняться нулю.

Пусть в объеме V, ограниченном поверхностью S, имеется заряд q с объемной плотностью (рис. 7.4).

Если через поверхность S вытекает ток i, то заряд q начнет уменьшаться со скоростью:

.

Ток .

Получаем уравнение непрерывности в интегральной форме:

 — закон сохранения заряда.

Выведем уравнение непрерывности в дифференциальной форме. Выразим заряд q через объемную плотность . Тогда получим:

. (7.1)

По теореме Остроградского:

. (7.2)

Из (7.1) с учетом (7.2) можно записать:

.

Отсюда . (7.3)

Дивергенция плотности тока проводимости равна скорости убывания плотности объемных зарядов.

О чем это уравнение говорит? Прежде всего о том, что плотность тока проводимости может иметь источники и стоки в виде изменяющихся во времени объемных зарядов.