
- •Теоретические основы электротехники Электромагнитное поле
- •Рецензенты:
- •Учебное издание
- •Теоретические основы электротехники Электромагнитное поле
- •428015 Чебоксары, Московский просп., 15 Введение
- •Глава 1. Общие сведения
- •Основные векторы электромагнитного поля и макроскопические параметры
- •Вектор напряженности электрического поля .
- •2. Вектор электрического смещения .
- •4. Вектор электрической поляризации .
- •5. Вектор намагниченности .
- •6. Вектор магнитной индукции .
- •1.2. Система уравнений максвелла для электромагнитного поля
- •Первое уравнение максвелла
- •Физический смысл первого уравнения Максвелла.
- •Непрерывность токов проводимости и токов смещения
- •Второе уравнение максвелла
- •Третье уравнение максвелла
- •Четвертое уравнение максвелла
- •Полная система уравнений максвелла
- •Теорема о единственности решений системы уравнений максвелла
- •Глава 2. Электростатическое поле
- •2.1 Основные понятия и определения
- •Напряжение, потенциал и разность потенциалов в электростатическом поле
- •2.2 Теорема гаусса в интегральной форме при расчете электростатических полей
- •2.3. Уравнения пуассона и лапласа
- •Проводники в электростатическом поле
- •2.4. Граничные условия в электростатическом поле
- •2.5. Задачи электростатики
- •2.6 Метод зеркальных изображений при решении задач электростатики
- •Глава 3.Емкость. Примеры расчета емкостей
- •3.1. Емкость плоского конденсатора
- •3.2. Емкость двухслойного плоского конденсатора
- •3.6. Поле и емкость двухпроводной линии
- •3.7. Емкость системы несоосных проводов
- •3.8. Емкость системы «провод-земля»
- •3.9. Поле двух заряженных проводов, находящихся над поверхностью земли
- •Глава 4. Энергия и силы электростатического поля
- •4.1. Энергия взаимодействия точечных зарядов
- •4.2. Энергия электростатического поля
- •4.3. Силы, действующие в электрическом поле
- •Глава 5.Электрическое поле постоянного тока в проводящей среде
- •5.1. Основные законы
- •Закон ома в дифференциальной форме
- •Первый закон кирхгофа в диффеннциальной форме
- •Рассмотрим иной вариант доказательства.
- •Закон джоуля-ленца в дифференциальной форме
- •5.2. Поле полусферического электрода
- •5.3.Граничные условия в электростационарном поле
- •5.4. Аналогия между электрическим полем постоянного тока и электростатическим полем
- •Глава 6.Магнитное поле, постоянное во времени.
- •6.1. Основные понятия и законы
- •Вектор напряженности магнитного поля
- •З аконы ампера и био — савара
- •Магнитный поток и его непрерывность
- •Закон полного тока для стационарного магнитного поля
- •6.2. Граничные условия в магнитном поле
- •Закон преломления вектора
- •6.3 Векторный потенциал магнитного поля
- •6.4. Скалярный магнитный потенциал
- •6.5. Аналогия между магнитным полем постоянного тока и полем электростатики
- •Связь между магнитным потоком и векторным потенциалом
- •6.6.Энергия и силы магнитного поля.
- •6.7. Индуктивность
- •6.8. Взаимоиндуктивность
- •6.9. Методы расчета магнитных полей
- •Метод зеркальных изображений для расчета магнитного поля
- •7.1. Полный электрический ток и его непрерывность
- •Непрерывность полного тока
- •7.2. Уравнения максвелла в комплексной форме
- •7.3.Теорема умова — пойнтинга
- •- Теорема Умова — Пойнтинга.
- •7.4. Теорема умова — пойнтинга в комплексной форме
- •Глава 8. Плоские электромагнитные волны
- •8.1. Уравнения плоской волны
- •8.2. Свойства плоских волн
- •Выводы:
- •8.3. Распространение плоской электромагнитной волныв проводящей среде
- •8.4. Поверхностный эффект
- •8.5. Экранирование в переменном электромагнитном поле
- •8.6. Распространение плоской электромагнитной волны в идеальном диэлектрике
- •Глава 9. Векторы и потенциалы переменного электромагнитного поля
- •9.1. Уравнения для векторов переменного эмп
- •9.2. Потенциалы переменного эмп
- •9.3. Уравнения для электродинамического потенциала
- •9.4. Запаздывающие и опережающие потенциалы переменного электромагнитного поля.
- •Комплексная форма записи запаздывающего потенциала
- •Понятие о квазистационарном и квазистатическом полях
- •Список рекомендуемой литературы Основная
- •Дополнительная
- •Оглавление
- •Глава 1. Общие сведения 6
- •Глава 2. Электростатическое поле 18
- •Глава 3. Емкость. Примеры расчета емкостей 35
6.7. Индуктивность
Индуктивностью проводника с током называется величина
 ,
где
,
где
 - ток;
- ток;
 - потокосцепление.
- потокосцепление.
П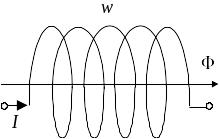 отокосцепление —
это произведение потока
на число
,
указывающее, сколько раз поток
сцеплен с током, его вызвавшим.
отокосцепление —
это произведение потока
на число
,
указывающее, сколько раз поток
сцеплен с током, его вызвавшим.
Например, для катушки, приведенной на рис. 6.26,

87
,г
Рис. 6.26
де и совпадает с числом витков катушки.
и совпадает с числом витков катушки.
Индуктивность
зависит от магнитной проницаемости
 и геометрических размеров проводника
и измеряется в генри (Гн).
и геометрических размеров проводника
и измеряется в генри (Гн).
Пример 1. Определить внутреннюю и внешнюю индуктивности цилиндрического проводника с радиусом а и длиной l (рис. 6.27).
Выберем площадку dS на радиусе r. Поток через эту площадку
 .
.
В еличину
определим из закона полного тока:
еличину
определим из закона полного тока:
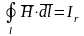 ,
,
где
 —
полный ток, заключенный в цилиндре
радиуса r.
—
полный ток, заключенный в цилиндре
радиуса r.
При
поток
 сцепляется со всем током I
один раз, т. е.
сцепляется со всем током I
один раз, т. е.
Рис. 6.27  ,
а при
,
а при
 поток
сцепляется лишь с частью тока
,
равной
поток
сцепляется лишь с частью тока
,
равной
 ,
,
что значит
 .
.
Приращение
 ,
а потокосцепление
,
а потокосцепление
 .
.
При
 .
.
При
 .
.
Внутренняя индуктивность
 .
.
Как видно, внутренняя индуктивность не зависит от радиуса провода.
Внешняя индуктивность:
 .
.
Внешний поток
сцепляется с током I
один раз (рис. 6.28), поэтому
 .
.

Рис. 6.28
;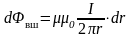 ;
;
 .
.
При
 .
.
Значит,
внешняя индуктивность уединенного
провода равна
 .
.
Пример 2. Определить индуктивность двухпроводной линии (рис. 6.29). Расстояние между осями d, радиусы проводов a.
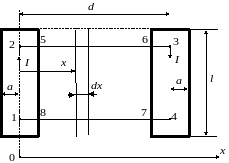
Рис. 6.29
Магнитный поток, сцепленный с линией, состоит из трех потоков:
 .
.
Магнитную индукцию найдем как сумму индукций отдельных проводов по методу наложения. Первый и третий потоки — внутренние, а второй — внешний.
Внутреннее
потокосцепление:
 .
Суммарное внутреннее потокосцепление:
.
Суммарное внутреннее потокосцепление:
 .
.
Найдем внешнее
потокосцепление. По закону полного
тока —
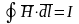 —
найдем напряженность поля одного тока
(провода):
—
найдем напряженность поля одного тока
(провода):
 ,
где
,
где
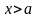 .
.
Поток одного провода:
 .
.
Поскольку
 ,
то
,
то
 .
.
Индуктивность
 .
.
6.8. Взаимоиндуктивность
Для
характеристики степени магнитной связи
контуров вводится понятие взаимоиндуктивности.
Взаимоиндуктивностью называется
величина, равная
 или
или
 ,
,
где
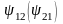 —
потокосцепление потока
—
потокосцепление потока
 ,
вызванного током
,
вызванного током
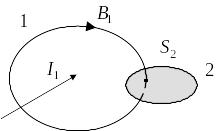
 с контуром 2(1) (рис. 6.30).
с контуром 2(1) (рис. 6.30).
 .
.
Рис. 6.30
В случае двух индуктивно связанных цепей с токами и энергия магнитного поля:
 ,
,
где
 —
потокосцепления взаимной индукции,
обусловленные соответственно токами
и
:
—
потокосцепления взаимной индукции,
обусловленные соответственно токами
и
:
 ,
,
 .
.
Для
определения
 можно воспользоваться
(векторным потенциалом магнитного поля)
(рис. 6.31).
можно воспользоваться
(векторным потенциалом магнитного поля)
(рис. 6.31).
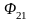 через
контур
через
контур
 :
:
 .
.
О
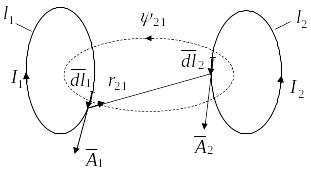
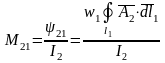 ,
,
г
Рис. 6.31
де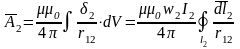 .
.
Итак:
 .
.
П ример 1.
Рассчитать
взаимную индуктивность между проводом
и рамкой (рис. 6.32).
ример 1.
Рассчитать
взаимную индуктивность между проводом
и рамкой (рис. 6.32).
Провод и рамка находятся в одной плоскости.
 ;
;
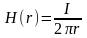 ;
;
 ;
;
91
Рис. 6.32
 ;
;
 ;
;
 .
.
П ример 2.
Определить взаимную индуктивность
между двумя слоями обмотки катушки
длиной l и радиусом
R (lR),
если число витков первого слоя равно
w1, а второго
слоя — w2
(рис. 6.33).
ример 2.
Определить взаимную индуктивность
между двумя слоями обмотки катушки
длиной l и радиусом
R (lR),
если число витков первого слоя равно
w1, а второго
слоя — w2
(рис. 6.33).
Будем считать катушку с двухслойной обмоткой соленоидом.
Т
Рис. 6.33
огда магнитное поле внутри катушки будет практически однородным.
Воспользуемся алгоритмом определения взаимной индуктивности.
1. Используя
закон полного тока, найдем значение
магнитной индукции В1, создаваемой
током I в слое с числом
витков w1. В центре
на оси катушки имеем  .
.
2. Найдем площадку
S2, через которую
замыкается поток магнитной индукции.
Эта площадка ограничена витками второго
слоя. Считая толщину слоев обмотки
намного меньше радиуса катушки, получим
 .
.
3. Рассчитаем
поток вектора магнитной индукции
 сквозь выбранную площадку S2
сквозь выбранную площадку S2
 .
.
4. Найдем потокосцепление второго слоя с числом витков w2
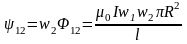 .
.
5. Определим
взаимную индуктивность
 .
.
Результат получится аналогичным, если предположить, что ток I протекает по слою с числом витков w2 и определить М21.
Пример 3. Взаимная индуктивность двух линий длиной l (рис. 6.34).
П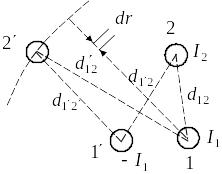 ровода
ровода
 параллельны
параллельны
 :
:
.
Если диаметры проводов второй линии очень малы, то
 ,
,
г
Рис. 6.34
де — магнитный поток от тока провода 1,  —
магнитный поток от тока провода
—
магнитный поток от тока провода
 .
.
Если провести радиальную полуплоскость, то она будет перпендикулярна линиям магнитной индукции.
На расстоянии r от оси провода 1:
 ;
;
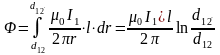 .
.
Аналогично для
провода
с током
 :
:
 ;
;

93
;
 .
.
Тот же результат
можно получить, если задаться током
тонких проводов второй линии и искать
 .
.
Полученный результат не изменится, если тонкие провода заменить реальными, так как М не зависит от диаметра проводов, а также от их сечения (сплошные или трубчатые).
