6.2. Граничные условия в магнитном поле

Р ассмотрим границу двух сред с различными (рис. 6.17). Площадки считаем малыми, поэтому на них вектор одинаков. Исходя из непрерывности магнитного потока, имеем

.

Нормальные составляющие потоков определяются выражениями:

,

.

При уменьшении высоты цилиндра до нуля так, чтобы совпали с границей раздела, получим . Тогда

.

Нормальная составляющая вектора индукции магнитного поля на границе двух сред непрерывна.

Так как ,

,

то .

Д ля вывода второго граничного условия составим циркуляцию вектора вдоль контура , расположенного вблизи границы (рис. 6.18), где .

По закону полного тока:

.

Представив левую часть уравнения в виде суммы, получим: Рис. 6.18

.

Уменьшая длину боковых сторон так, чтобы участки совпали с граничной поверхностью, получим

.

Если по граничной поверхности течет ток с поверхностной плотностью , то

.

Тогда

На границе двух сред касательная составляющая вектора напряженности магнитного поля претерпевает скачок, равный плотности поверхностного тока, протекающего по границе.

Если =0, т. е. по граничной поверхности ток не протекает, то,

.

Учитывая, что

, ,

имеем .

Закон преломления вектора

Из прямоугольных треугольников (рис. 6.19):

; ;

;

или . Рис. 6.19

6.3 Векторный потенциал магнитного поля

Векторным потенциалом называется величина , которая определяется как

. (6.4)

Поскольку это выражение векторный потенциал определяет не однозначно, то необходимо задать дивергенцию .

Будем считать, что . Подставим в первое уравнение Максвелла ( ) выражение для , полученное из (6.4):

, откуда .

Известно, что , где (по условию). Тогда .

Т аким образом, векторный потенциал магнитного поля определяется по уравнению Пуассона, т. е. введение позволяет свести исходное уравнение к известным стандартным уравнениям Пуассона и Лапласа.

Решение уравнения Пуассона имеет вид:

Рис. 6.20

,

где r — расстояние от точки N, в которой определяется , до элементов объема (рис. 6.20), на которые разбит весь объем с током;

 — плотность постоянного тока.

Направление векторного потенциала всегда совпадает с направлением вектора плотности тока .

Если ток течет по линейному проводнику (рис. 6.21), то

Рис. 6.21

,

т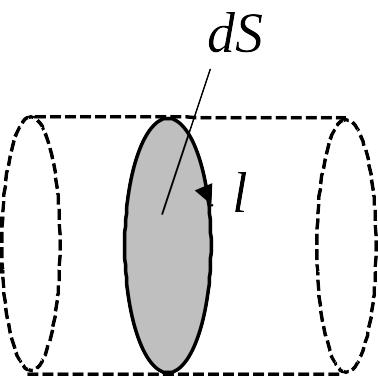 огда .

Пример 1. Определить векторный потенциал одиночного электрического провода с радиусом a и током I (рис. 6.22).

Непосредственно из определения следует, что . (6.5)

Совместим ось z цилиндрической системы координат с осью проводника.

Т

Рис. 6.22

огда , а ; .

Из (6.5) имеем .

Рассмотрим поле внутри и вне провода.

а) Внутри провода:

.

Если принять, что при имеем , то

;

.

б) Вне провода:

;

.

Пример 2. Получить уравнение Био — Савара с помощью векторного потенциала.

;

,

т

81

ак как производная от .

6.4. Скалярный магнитный потенциал

Для области, где отсутствуют постоянные токи, справедливо соотношение

(так как ). (6.6)

Кроме того, в магнитном поле всегда

.

Если справедливо (6.6), то вектор можно представить в виде:

,

где  — скалярный векторный потенциал

Учитывая, что ,

получим - уравнение Лапласа для скалярного магнитного потенциала.

Разность магнитных потенциалов

 — магнитное напряжение.

В качестве пути интегрирования целесообразно выбирать путь по силовой линии или эквипотенциальной линии.

Пример. Имеется провод с током I (рис. 6.23). Определить магнитное напряжение между точками А и В.

У

I

Рис. 6.23

читывая, что зависит от пути интегрирования, получим