Глава 6.Магнитное поле, постоянное во времени.

6.1. Основные понятия и законы

Из физики известно, что постоянное во времени магнитное поле вызывается постоянным током или постоянными магнитами. Для изучения свойств магнитного поля и количественного его описания вводится вектор магнитной индукции .

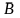При исследовании магнитного поля пользуются небольшим плоским пробным контуром с постоянным током (рис. 6.1) так же, как при исследовании электростатического поля используется пробный заряд.

П робный контур, внесенный в магнитное поле, под действием сил поля примет определенное устойчивое положение, которое называют равновесным. Направление положительной

Рис. 6.1 нормали к площади контура в устойчиво равновесном положении считают направлением вектора поля в данном месте. Положительное направление нормали и направление тока в контуре связаны правилом правоходового винта (буравчика).

Е сли в магнитное поле ввести линейный проводник dl с током I (рис. 6.2), то сила, действующая на него будет равна

.

Рис. 6.2

Исходя из этого выражения, можно дать определение индукции как силы, действующей на проводник единичной длины, если по нему протекает ток, равный одному амперу.

(Напомним, что направление можно определить по правилу левой руки: ладонь левой руки надо расположить так, чтобы в нее

68

входили силовые линии вектора , четыре пальца направить по току, тогда повернутый на 90 большой палец покажет направление действия силы .)

Л инией вектора называют линию, в каждой точке которой вектор направлен по касательной (рис. 6.3).

В случае поля прямого провода с током линии вектора будут окружностями, лежащими в плоскости, перпендикулярной проводу и с центром на оси провода. Индукция В будет одинаковой на этой линии. Рис. 6.3

Вектор напряженности магнитного поля

Связь между индукцией и напряженностью в вакууме вычисляют следующим образом:

,

где Гн/м — магнитная постоянная.

Если проводник находится в некоторой среде, то его магнитное поле будет отличаться от поля в вакууме. Под действием магнитного поля тока I среда намагничивается. Намагниченное вещество создает свое собственное поле с индукцией . Магнитная индукция результирующего поля . Напряженность же поля остается такой же. Магнитная индукция тогда может быть записана как

,

где  — абсолютная магнитная проницаемость вещества. Ее удобно определить относительно проницаемости вакуума , где  — относительная магнитная проницаемость.

69

С учетом этого можно записать:

.

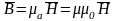Индукция измеряется в теслах (Тл), напряженность  — А/м.

З аконы ампера и био — савара

Рассматривая взаимодействие двух проводников с током (рис. 6.4), Ампер в 1820 г. установил:

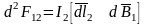, (6.1)

где  — сила взаимодействия между двумя элементарными участками двух

Рис. 6.4 проводников с токами.

 — индукция в месте нахождения участка от действия участка 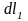с током .

Таким образом, сила взаимодействия между двумя проводниками с токами равна

.

Д ля Био-Савар вывел выражение:

(6.2)

Это выражение справедливо для случая, если ток протекает по бесконечно тонкому проводнику.

Для случая объемного проводника (рис. 6.5)

.

Р

70

ис. 6.5

Т

71

71

огда (6.2) преобразуется к виду

. (6.3)

Подставляя (6.2) в (6.1), получим

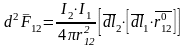 — закон Ампера.

Этот закон аналогичен закону Кулона в электростатике. Сила взаимодействия двух элементарных участков провода с токами аналогична силе взаимодействия двух элементарных зарядов.

Индукция, обусловленная объемным проводником с током, находится из (6.3):

.

Индукция, обусловленная замкнутым проводником с током (из 6.2), равна

.

Определим ток как ;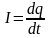

, где  — скорость зарядов.

Рис. 6.6

Если в качестве заряда взять заряд электрона, то  — сила Лоренца (рис. 6.6).

Это есть сила, с которой магнитное поле действует на единичный заряд, движущийся со скоростью .

Задача. По витку радиусом (рис. 6.7) протекает ток I, , Гн/м. Определить индукцию в центре.

;

, так как .

.

Рис. 6.7