
- •Теоретические основы электротехники Электромагнитное поле
- •Рецензенты:
- •Учебное издание
- •Теоретические основы электротехники Электромагнитное поле
- •428015 Чебоксары, Московский просп., 15 Введение
- •Глава 1. Общие сведения
- •Основные векторы электромагнитного поля и макроскопические параметры
- •Вектор напряженности электрического поля .
- •2. Вектор электрического смещения .
- •4. Вектор электрической поляризации .
- •5. Вектор намагниченности .
- •6. Вектор магнитной индукции .
- •1.2. Система уравнений максвелла для электромагнитного поля
- •Первое уравнение максвелла
- •Физический смысл первого уравнения Максвелла.
- •Непрерывность токов проводимости и токов смещения
- •Второе уравнение максвелла
- •Третье уравнение максвелла
- •Четвертое уравнение максвелла
- •Полная система уравнений максвелла
- •Теорема о единственности решений системы уравнений максвелла
- •Глава 2. Электростатическое поле
- •2.1 Основные понятия и определения
- •Напряжение, потенциал и разность потенциалов в электростатическом поле
- •2.2 Теорема гаусса в интегральной форме при расчете электростатических полей
- •2.3. Уравнения пуассона и лапласа
- •Проводники в электростатическом поле
- •2.4. Граничные условия в электростатическом поле
- •2.5. Задачи электростатики
- •2.6 Метод зеркальных изображений при решении задач электростатики
- •Глава 3.Емкость. Примеры расчета емкостей
- •3.1. Емкость плоского конденсатора
- •3.2. Емкость двухслойного плоского конденсатора
- •3.6. Поле и емкость двухпроводной линии
- •3.7. Емкость системы несоосных проводов
- •3.8. Емкость системы «провод-земля»
- •3.9. Поле двух заряженных проводов, находящихся над поверхностью земли
- •Глава 4. Энергия и силы электростатического поля
- •4.1. Энергия взаимодействия точечных зарядов
- •4.2. Энергия электростатического поля
- •4.3. Силы, действующие в электрическом поле
- •Глава 5.Электрическое поле постоянного тока в проводящей среде
- •5.1. Основные законы
- •Закон ома в дифференциальной форме
- •Первый закон кирхгофа в диффеннциальной форме
- •Рассмотрим иной вариант доказательства.
- •Закон джоуля-ленца в дифференциальной форме
- •5.2. Поле полусферического электрода
- •5.3.Граничные условия в электростационарном поле
- •5.4. Аналогия между электрическим полем постоянного тока и электростатическим полем
- •Глава 6.Магнитное поле, постоянное во времени.
- •6.1. Основные понятия и законы
- •Вектор напряженности магнитного поля
- •З аконы ампера и био — савара
- •Магнитный поток и его непрерывность
- •Закон полного тока для стационарного магнитного поля
- •6.2. Граничные условия в магнитном поле
- •Закон преломления вектора
- •6.3 Векторный потенциал магнитного поля
- •6.4. Скалярный магнитный потенциал
- •6.5. Аналогия между магнитным полем постоянного тока и полем электростатики
- •Связь между магнитным потоком и векторным потенциалом
- •6.6.Энергия и силы магнитного поля.
- •6.7. Индуктивность
- •6.8. Взаимоиндуктивность
- •6.9. Методы расчета магнитных полей
- •Метод зеркальных изображений для расчета магнитного поля
- •7.1. Полный электрический ток и его непрерывность
- •Непрерывность полного тока
- •7.2. Уравнения максвелла в комплексной форме
- •7.3.Теорема умова — пойнтинга
- •- Теорема Умова — Пойнтинга.
- •7.4. Теорема умова — пойнтинга в комплексной форме
- •Глава 8. Плоские электромагнитные волны
- •8.1. Уравнения плоской волны
- •8.2. Свойства плоских волн
- •Выводы:
- •8.3. Распространение плоской электромагнитной волныв проводящей среде
- •8.4. Поверхностный эффект
- •8.5. Экранирование в переменном электромагнитном поле
- •8.6. Распространение плоской электромагнитной волны в идеальном диэлектрике
- •Глава 9. Векторы и потенциалы переменного электромагнитного поля
- •9.1. Уравнения для векторов переменного эмп
- •9.2. Потенциалы переменного эмп
- •9.3. Уравнения для электродинамического потенциала
- •9.4. Запаздывающие и опережающие потенциалы переменного электромагнитного поля.
- •Комплексная форма записи запаздывающего потенциала
- •Понятие о квазистационарном и квазистатическом полях
- •Список рекомендуемой литературы Основная
- •Дополнительная
- •Оглавление
- •Глава 1. Общие сведения 6
- •Глава 2. Электростатическое поле 18
- •Глава 3. Емкость. Примеры расчета емкостей 35
5.4. Аналогия между электрическим полем постоянного тока и электростатическим полем
П редположим,
что между двумя параллельными проводниками
приложено напряжение U
(рис. 5.10). Проводимость провода
редположим,
что между двумя параллельными проводниками
приложено напряжение U
(рис. 5.10). Проводимость провода
 ,
проводимость среды между пластинами —
,
проводимость среды между пластинами —
 .
Нормальная составляющая вектора
напряженности
.
Нормальная составляющая вектора
напряженности
 равна
равна
 ,
плотность тока в диэлектрике
,
плотность тока в диэлектрике
 .
.
Рис. 5.10
Положим,
что проводники замкнуты помимо
диэлектрика, тогда по ним течет ток с
плотностью
 ,
т. е. на поверхности проводника при
этом появляется тангенциальная
составляющая поля
,
т. е. на поверхности проводника при
этом появляется тангенциальная
составляющая поля
 .
Как правило, проводимость проводника
намного больше проводимости диэлектрика
.
Как правило, проводимость проводника
намного больше проводимости диэлектрика
 .
В связи с этим при рассмотрении поля
постоянного тока между проводниками
принимается равной нулю.
.
В связи с этим при рассмотрении поля
постоянного тока между проводниками
принимается равной нулю.
При таком предположении поле постоянного тока тождественно полю в условиях электростатики.
Действительно, из принципа непрерывности тока следует
 .
.
В то же время по
закону Ома
.
Тогда
 или
или
 .
Поскольку
.
Поскольку
 ,
то
,
то
 ,
.
,
.
Как видим, потенциал поля в области между проводниками определяется уравнением Лапласа:
.
Электростатическое поле в диэлектрике без свободных зарядов описывается также уравнением Лапласа. Поэтому, если две ограниченные области — проводящая (без сторонних сил) и электрическая (без свободных электрических зарядов) — имеют на граничной поверхности одинаковое распределение потенциалов, то внутри каждой из них распределение потенциала будет одинаковым.
По своей физической природе поля электростатическое и постоянного тока в проводящей среде различны: электростатическое поле — поле неподвижных в пространстве и неизменных во времени зарядов; поле в проводящей среде — поле движущихся зарядов. Тем не менее, между математическими моделями этих полей можно провести формальную аналогию.
Электростатическое
поле при
|
|
Электромагнитное поле постоянного тока при
|
|
|
|
|
|
|
|
|
(всегда) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(всегда) |
|
|
|
|
|
|
Благодаря такой аналогии, можно формулы, полученные при расчете электростатических полей, использовать для расчета поля постоянного тока. В частности, проводимость в поле постоянного тока можно вычислять по формулам для емкости в электростатическом поле. Достаточно заменить емкость на проводимость, абсолютную диэлектрическую проницаемость — на удельную проводимость.
П ример 1. Рассчитать
проводимость коаксиального кабеля
(рис. 5.11). Пространство между жилой и
оболочкой заполнено неидеальным
диэлектриком с
,
радиус жилы
,радиус
оболочки
.
ример 1. Рассчитать
проводимость коаксиального кабеля
(рис. 5.11). Пространство между жилой и
оболочкой заполнено неидеальным
диэлектриком с
,
радиус жилы
,радиус
оболочки
.
Рис. 5.11
Алгоритм расчета условно можно представить в следующем виде
 .
.
Плотность тока в
произвольной точке с радиусом r
будет
 .
Следовательно,
.
Следовательно,
 .
.
 .
.
Тогда
проводимость
 ,
а, используя аналогию, можно записать
формулу для расчета емкости коаксиального
кабеля
,
а, используя аналогию, можно записать
формулу для расчета емкости коаксиального
кабеля
 .
.
Пример 2. Определить проводимость растекания тока в сферическом заземлителе (рис. 5.12).
Воспользуемся аналогией — шар в электростатике (рис. 5.13)
Рис. 5.12 Рис. 5.13
Поскольку
 ,
то нет тангенциальной составляющей
поля, а есть только радиальная. Поверхность
шара — эквипотенциаль.
,
то нет тангенциальной составляющей
поля, а есть только радиальная. Поверхность
шара — эквипотенциаль.
Е
мкость сферы —
 ,
а по аналогии проводимость сферического
заземлителя —
,
а по аналогии проводимость сферического
заземлителя —
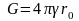 .
.




 (всегда)
(всегда)




 (всегда)
(всегда)





