Глава 4. Энергия и силы электростатического поля

4.1. Энергия взаимодействия точечных зарядов

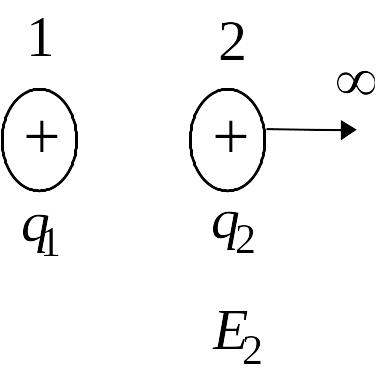
Для того чтобы приблизить два одноименных заряда и (рис. 4.1), необходимо совершить работу против кулоновских сил отталкивания. Энергия взаимодействия двух зарядов равна этой работе. Если один из зарядов остается неподвижным, а другой будет перемещаться, то силы

поля совершат работу по перемещению заряда за счет Рис. 4.1

убыли энергии взаимодействия. И если один из них переместится в бесконечность, то совершенная при этом работа будет равна всей энергии взаимодействия.

При перемещении заряда из точки 2, в которой напряженность поля равна , в бесконечность, работа сил поля равна

,

где  — вектор напряженности поля, создаваемого зарядом .

Так как потенциал в точке 2 от заряда равен

,

то, сравнивая эти два выражения, приходим к выводу, что выполненная работа равна

,

а энергия взаимодействия равна ей и противоположна по знаку:

49

.

При перемещении заряда из точки 1 в бесконечность совершается такая же работа.

; ,

поэтому .

Удобно записывать как .

Можно показать, что в случае n зарядов

(4.1)

Энергия системы заряженных тел равна полусумме произведений потенциалов тел на их заряды. Единицей энергии является джоуль (Дж).

4.2. Энергия электростатического поля

Предположим, что энергия электростатического поля обусловлена объемными и поверхностными зарядами. Тогда

. (4.2)

Выражение (4.2) отражает полную энергию электрического поля. Его можно видоизменить. Для этого воспользуемся следующим соотношением, известным из теории поля

.

Проинтегрируем обе части этого уравнения, перемножив на 1/2:

.

Поскольку (теорема Гаусса) и ,

то с учетом (теорема Остроградского)

получим . (4.3)

Н а поверхности проводника при (рис. 4.2) из граничных условий:

, проводник: , поэтому Рис. 4.2

и выражение (4.3) запишется в виде:

.

Отсюда

. (4.4)

Сравнивая выражения (4.4) и (4.2), получим

.

Физический смысл этого уравнения заключается в том, что носителем энергии является электрическое поле, причем энергия распределена с объемной плотностью

.

Если напряженность отлична от нуля, то силы поля могут совершать работу за счет энергии поля.

Выражение эквивалентно выражению , которое было получено на основании закона сохранения энергии. Если поле создается неподвижными зарядами, то можно пользоваться любым из этих выражений. Энергия электрического поля движущегося электрического заряда определяется из выражения (4.4).

4.3. Силы, действующие в электрическом поле

Если заряженные тела меняют свое положение в пространстве, то энергия электрического поля изменяется (изменяются потенциалы или заряды).

Рассмотрим поле заряженных проводников. Будем считать, что они перемещаются очень медленно, и магнитные явления можно не принимать в расчет (напомним, что при движении заряженных тел возникает магнитное поле). Перемещение зарядов может совершаться как силами поля, так и внешними силами. При этом могут встречаться два случая:

1. Заряды при перемещении остаются неизменными (например, при перемещении предварительно заряженных обкладок конденсатора заряды не изменяются).

2. Перемещение происходит при неизменных потенциалах (перемещение обкладок, подключенных к источнику постоянного напряжения).

Рассмотрим эти случаи подробнее.

Случай 1. Пусть q=const. Если перемещение зарядов происходит за счет сил поля на бесконечно малое расстояние, то работа сил поля равна и на уменьшается энергия поля. По закону

сохранения энергии:

.

Следовательно,

.

Если работу совершают внешние силы, то энергия поля возрастает на величину

,

что означает: потенциалы всех точек возрастут, но заряды останутся неизменными.

Случай 2. Пусть =const. Проводники соединены с источниками энергии. При этом энергия, отдаваемая источниками , должна быть равна работе сил поля по перемещению заряженных тел и приращению энергии поля:

.

Если заряд k-го тела изменится на , то энергия, отданная источником, равна .

Для системы n зарядов

.

Изменение энергии электрического поля:

.

Работа сил поля

.

Вывод. Энергия, отдаваемая источником, затрачивается поровну на работу сил поля и на изменение энергии электрического поля.

Если перемещение происходит за счет работы внешних сил, то

53

источник получит энергию:

.

Силу, действующую на заряженное тело (в направлении l), можно определить как

.

Если , то , поэтому

и

Вывод. Сила действует всегда в том направлении, в каком уменьшается энергия поля.

В электрическом поле сила действует не только на проводники, но и на диэлектрики. Причем заметим, что она направлена от диэлектрика с высокой проницаемостью к диэлектрику с меньшей проницаемостью, поскольку плотность энергии в диэлектрике с больше, чем в диэлектрике с .