3.6. Поле и емкость двухпроводной линии
П
41
ровода реальной линии имеют конечные сечения. При этом заряды по поверхности проводников распределяются с неодинаковой плотностью. Причем закон распределения заряда в общем случае неизвестен, что осложняет решение задачи. Однако в важном частном случае для проводов круглого сечения задача может быть решена точно, если заметить (как только что доказали), что в поле двух заряженных осей все поверхности равного потенциала
являются поверхностями цилиндров (рис. 3.8). Всегда можно так расположить оси линейных проводов, чтобы две поверхности равного потенциала совпали с поверхностями реальных проводов.
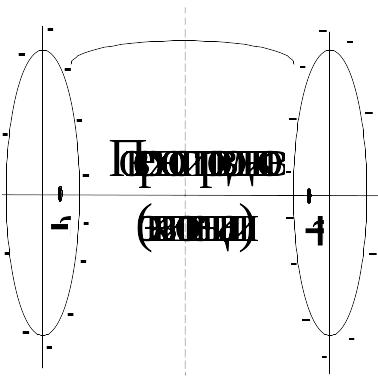
Рис. 3.8
Поле внутри металлических проводов будет отсутствовать. Поле же в диэлектрике при такой замене реальных проводов эквивалентными нитями останется без изменения, так как при этом удовлетворяется основное граничное условие — постоянство потенциалов на поверхности проводов.
Таким образом, задача расчета поля двух проводов круглого сечения, а также несоосных цилиндров сводится к отысканию положения эквивалентных им заряженных осей, или, другими словами, электрических осей.
Перейдем к рассмотрению емкости двухпроводной линии (рис. 3.9).
Рис. 3.9
Д
42
анная система проводов приводится к эквивалентной системе разноименно заряженных осей. Причем место расположения этих осей не совпадает с геометрическими осями проводов. Заряженные оси располагаются так, что поверхности проводников
представляют собой эквипотенциальные поверхности для заряженных осей.
(3.3)
Из данной системы
определяем
,
и b.
Далее рассматривается задача расчета поля двух заряженных осей. Потенциалы точек 1 и 2 с учетом ранее выведенных выражений запишутся
.
;
Емкость на единицу длины равна
.
Частный случай: 
.
.
Если
,
то
,
,
тогда
.
3.7. Емкость системы несоосных проводов
Зададимся линейной плотностью заряда + на внутреннем проводе.
Рис. 3.10
Эта система сводится к полю заряженных осей (рис. 3.10), координаты которых определяются из системы уравнений:
С учетом того, что поверхности проводников являются эквипотенциальными поверхностями, потенциалы точек 1 и 2 запишутся
;
;
.
Емкость на единицу длины
.
3.8. Емкость системы «провод-земля»
Дано: r, , h (рис. 3.11).
Найти: .
Решение. Пусть провод заряжен с линейной плотностью .
Считая
,
емкость
можно найти из выражения
Рис. 3.11
Для определения
используем метод зеркальных изображений,
позволяющий свести задачу к рассмотрению
поля двух заряженных осей (рис. 3.12).
Тогда
;
.
Если
,
то
.
Тогда
.
Рис. 3.12
3.9. Поле двух заряженных проводов, находящихся над поверхностью земли
В этом случае часто пользуются системой уравнений с потенциальными и емкостными коэффициентами, которую можно получить на основе метода зеркальных изображений.
Дано:
,
,
,
,
,
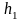d, r
(рис. 3.13).
Найти:
частичные и рабочие емкости линии.
Решение. Предположим, что
.
Э
Рис. 3.13
ти допущения позволяют сделать вывод о совпадении электрических и геометрических осей.
По методу наложения.
;
,
где
;
;
;
.
Введя потенциальные коэффициенты , потенциалы проводов можно определить из следующих выражений:
(3.4)
где 
;
;
;
и
- взаимные потенциальные коэффициенты,
46
и
- собственные потенциальные коэффициенты.
Такая система называется системой с потенциальными коэффициентами. Она позволяет связать линейные плотности зарядов на проводниках с потенциалами, возникающими на этих проводах.
Если задача обратная, то есть даны потенциалы проводников, а нужно найти линейные плотности зарядов, которые возникают на проводах, то используется система с емкостными коэффициентами.
(3.5)
Из решения уравнений (3.4) можно получить
.
Сравнивая полученное выражение с аналогичным в уравнениях (3.5), найдем
.
Аналогично из уравнений (3.5) имеем
.
Сравнивая полученное выражение с аналогичным в уравнениях (3.5), найдем
.
Коэффициенты
и
называются собственными
емкостными коэффициентами. Они всегда положительные.
Коэффициенты
и
называются взаимными емкостными
коэффициентами. Они всегда меньше нуля,
так как наведенный заряд имеет
противоположный знак тому заряду,
который его вызвал.
П
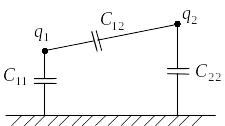
Линейные плотности зарядов Рис. 3.14 выражаются не через потенциалы, а
через разности потенциалов:
Отсюда
(4.6)
Сравнивая выражения (4.5) и (4.6), получим
; 
;
; 
.