5 6 Прямая геодезическая задача. По известным координатамх1 и у1 точки 1, дирекционному углу a1-2 и расстоянию d1-2 до точки 2 требуется вычислить ее координаты х2, у2.

Координаты точки 2 вычисляют по формулам (рис. 3.5):

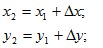 (3.4)

где Dх, Dу - приращения координат, равные

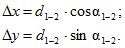 (3.5)

Обратная геодезическая задача. По известным координатам х₁, у₁ точки 1 и х₂, у₂ точки 2 требуется вычислить расстояние между ними d_1-2 и дирекционный угол a_1-2.

Из формул (3.5) и рис. 3.5 видно, что

. (3.6)

Для определения дирекционного угла a_1-2 воспользуемся функцией арктангенса. При этом учтем, что компьютерные программы и микрокалькуляторы выдают главное значение арктангенса

w = ,

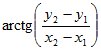лежащее в диапазоне -90°£w£+90°, тогда как искомый дирекционный угол a может иметь любое значение в диапазоне 0°£ a £ 360°.

Формула перехода от w к a зависит от координатной четверти, в которой расположено заданное направление или, другими словами, от знаков разностей Dy = y₂ - y₁ и Dx = х₂ - х₁ (см. таблицу 3.1 и рис. 3.6).

7 8 8. Рельеф и его изображение на картах.

Под рельефом местности понимают совокупность неровностей земной поверхности.

На топографических планах рельеф изображется горизонталями (0,1-0,15мм) Горизонталь- замкнутая кривая линия, изображающая геометрическое место точек земной поверхности с одинаковыми высотами. Расстояние между соседними горизонталями по отвесной линии называется высотой сечения рельефа. Расстояние между горизонталями в плане называется заложением.

Направление ската склона обозначается берх-штрихами – черточками длиной 0,5мм.

Для указания высот горизонталей их отметки подписывают в разрывах утолщенных 0,25мм горизонталей распологая основание цифр вниз по рельефу.

Различают следующие формы рельефа:

1) гора-возвышенность земной поверхности, имеющая коническую или куполообразную форму(выше 200м)

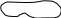
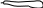
Небольшая гора называется холмом или бугром,а искусственный холм - курганом

2).Котловина - чашеобразное углубление земной поверхности. Небольшая котловина - яма

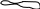
3). Хребет – возвышенность вытянутой формы с постепенным понижением имеет водораздельную линию

4). Лощина – вытянутое углубление местности постепенно понижающиеся. Имеет водозборнную линию

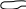
5). Седловина – место соединения двух лощин, расходящихся от одного хребта в противоположные стороны, и двух хребтов, идущих к двум различным вершинам

Равнина – поверхность земли, близкая к горизонтальной

9.Крутизна скатов.

О крутизне ската можно судить по величине заложений на карте. Чем меньше заложение (расстояние между горизонталями), тем круче скат. Для характеристики крутизны ската на местности используют угол наклона «ню». Чем больше угол наклона, тем круче скат. Другой характеристикой крутизны служит уклон. Уклоном линии местности наз. отношение превышения к горизонтальному проложению

_{Уклон безразмерная величина.Его выражают в % и промилле}

9 Определение площади аналитическим, графическим (геометрическим) и механическим способами.

При аналитическом способе площадь любого многоугольника, заданного координатами вершин вычисляется по следующим формулам:

Р = 1/2 Х_i (У_i+1 - У_i-1),

Р = 1/2 У_i (Х_i-1 - Х_i+1),

где i - порядковый номер вершин многоугольника, изменяющийся от 1 до N (числа вершин).

Относительная погрешность вычисления площади зависит в основном от погрешностей координат точек и составляет около 1/2000.

Графический способ определения площади предусматривает разбивку контура на элементарные геометрические фигуры (треугольники, четырехугольники и трапеции), площади которых вычисляют по измеренным на карте с учетом масштаба длинам сторон и высот. Относительная погрешность суммарной площади, полученной графически, обычно составляет более 0.5-1.0% (1/100).

Механический способ основан на применении специального прибора -полярного планиметра, который состоит из полюсного и обводного рычагов и счетного механизма. Перед измерением площади контура вычисляют цену деления планиметра с - площадь, соответствующую одному делению планиметра. Для этого на карте обводят планиметром один квадрат километровой сетки с известной площадью Р_изв.= 100 га. Отсчеты по счетному механизму берут до обводки n₁ и после обводки n₂, вычисляют их разность U, которую уточняют несколько раз.

Например, n₁ = 3546, n₂ = 4547. Тогда цена деления планиметра с = Р_изв./U = 100/1001=0.09990 га.

Площадь заданного контура сначала получают в результате обводки в делениях планиметра МU, а затем, используя цену деления с, - в гектарах Р = с ^. U. Контроль полученных результатов выполнятся повторными измерениями и вычислениями цены деления планиметра и определяемой площади. Относительная погрешность измерений площади планиметром составляет порядка 1/300.