
- •Интегральное исчисление функций нескольких переменных
- •I. Двойной интеграл
- •§1. Понятие двойного интеграла
- •1. Квадрируемые фигуры и их площади
- •2. Задача об объёме цилиндрического бруса
- •3. Определение двойного интеграла
- •4. Геометрический смысл двойного интеграла
- •5. Ограниченность интегрируемой функции
- •§2. Условия существования двойного интеграла
- •1. Нижняя и верхняя суммы Дарбу
- •2. Необходимое и достаточное условие интегрируемости
- •3. Интегрируемость непрерывной функции
- •§3. Основные свойства двойного интеграла
- •§4. Вычисление двойного интеграла повторным интегрированием
- •1. Повторные интегралы
- •2. Вычисление двойного интеграла
- •§5. Замена переменных в двойном интеграле
- •1. Отображение плоских областей
- •2. Площадь в криволинейных координатах
- •3. Замена переменной в двойном интеграле
- •4. Двойной интеграл в полярных координатах
4. Двойной интеграл в полярных координатах
Если преобразование стоит в переходе к полярным координатам, то формула (6) примет вид:
![]() .
.
Переход к полярным координатам эффективен, если уравнение границы области интегрирования или подынтегральная функция содержит выражение x2+y2.
Если в состав подынтегральной функции или уравнения границы области входит сумма вида ax2+by2 (a>0, b>0), то используют «обобщённую» полярную систему координат:
 ,
,
т огда
огда
![]() ,
а
,
а
![]() .
.
Пример 1.
Вычислить
![]() ,
где D-
часть круга x2+y2=R2,
лежащая в I четверти.
,
где D-
часть круга x2+y2=R2,
лежащая в I четверти.
Перейдём к полярным координатам
Область
 .
Следовательно,
.
Следовательно,


 .
.
П ример
2. Найти
площадь фигуры Р,
ограниченной параболами y=ax2,
y=bx2
(0<a<b)
и гиперболами xy=p,
xy=q
(0<p<q).
ример
2. Найти
площадь фигуры Р,
ограниченной параболами y=ax2,
y=bx2
(0<a<b)
и гиперболами xy=p,
xy=q
(0<p<q).
Площадь фигуры
![]() ,
но непосредственно вычислить этот
интеграл трудно. Поэтому следует
выполнить замену переменных.
,
но непосредственно вычислить этот
интеграл трудно. Поэтому следует
выполнить замену переменных.
Рассмотрим 2
семейства кривых: парабол y=ux2
(или
![]() )
и гипербол xy=v.
Чтобы каждое из них заполняло фигуру
Р,
достаточно взять какие u,
v, которые
удовлетворяют неравенствам aub,
pvq.
Через каждую точку фигуры Р
проходит
только одна парабола и только одна
гипербола. Следовательно, эти два
семейства кривых образуют сетку
координатных линий.
)
и гипербол xy=v.
Чтобы каждое из них заполняло фигуру
Р,
достаточно взять какие u,
v, которые
удовлетворяют неравенствам aub,
pvq.
Через каждую точку фигуры Р
проходит
только одна парабола и только одна
гипербола. Следовательно, эти два
семейства кривых образуют сетку
координатных линий.
Так как задание
этих двух кривых (то есть параметров u
и v)
однозначно определяет точку фигуры Р,
то u
и v
можно принять за криволинейные координаты
точек фигуры Р:
 (*)
(*)
Область Р перейдет в прямоугольник Q: aub, pvq на плоскости uOv, т.к.
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
Выразим из уравнений (*) x и y и найдем якобиан.



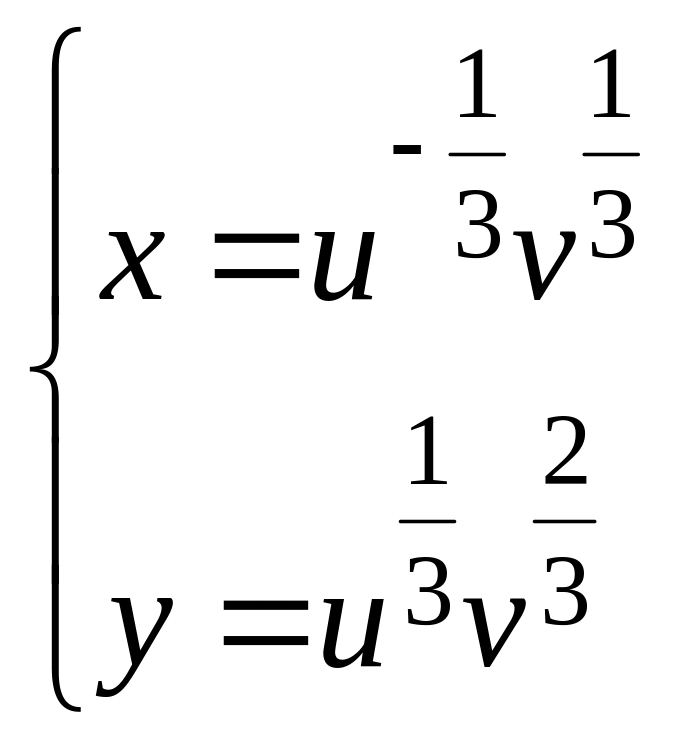


Тогда по формуле (5)
 .
.
