§5. Замена переменных в двойном интеграле

1. Отображение плоских областей

Рассмотрим 2 замкнутые области: G на плоскости UOV и D на плоскости XOY (каждая из этих областей может быть и не ограничена, в частности, может охватить всю плоскость). Пусть система функций

(1)

отображает взаимно однозначно область G на область D. Так как отображение взаимно однозначно, то функции (1) определяют систему функций

которые отображают область D на область G.

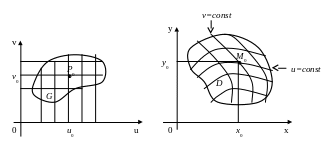Возьмём точку P₀(u₀;v₀)G. Проведём прямые u=u₀ и v=v₀. Система (1) отобразит Р₀ в точку M₀(x₀;y₀) D. Очевидно, прямая u=u₀ отобразится на некоторую кривую в плоскости XOY. Из (1) получим уравнение образа прямой u=u₀:

Эти формулы задают параметрические уравнения кривой. (Уравнение u(x;y)=u₀ - неявное уравнение той же кривой). Эта кривая называется кривой u=const. Придавая различные значения, будем получать различные линии u=const. Следовательно: u=const –семейство линий. Так как различные линии u=u₀ не пересекаются, то различные линии из семейства u=const тоже не пересекаются (так как отображение G на D взаимно однозначно).

Аналогично, образом прямой линии v=v₀ является кривая линия, уравнения которой

(неявное уравнение - v(x;y)=v₀). Эта линия называется v=const. Различные линии из семейства кривых v=const не пересекаются. Так как прямые u=u₀ и v=v₀ пересекаются в единственной точке P₀(u₀;v₀), а (1) – взаимно однозначное отображение G на D, то кривые u(x;y)=u₀ и v(x;y)=v₀ в плоскости XOY также пересекается в единственной точке M₀(x₀;y₀). Это означает, что числа u₀ и v₀ однозначно определяют точку M₀(x₀;y₀) на плоскости XOY. Значит, эти числа могут служить координатами этой точки. Числа u₀ и v₀ называются криволинейными координатами точки M₀ (так как координатные линии u=u₀ и v=v₀ на плоскости XOY являются кривыми линиями). Т.о., сетке декартовых координатных линий в плоскости UOV (два семейства перпендикулярных прямых) в плоскости XOY будет соответствовать сетка криволинейных линий, состоящая из двух семейств: u=const и v=const. Через любую точку M(x;y) пройдёт только одна координатная линия u=const и только одна координатная линия v=const.

u,v - криволинейные координаты точки М.

Тогда точка имеет прямоугольные координаты (x;y) и криволинейные координаты (u;v).

Примером криволинейных координат являются полярные координаты . Полярные координаты связаны с декартовыми известными соотношениями:

(2), .

Б удем рассматривать переменные  и  не как полярные координаты точки в плоскости XOY, а как прямоугольные координаты в другой плоскости O. Тогда формулы (2) отображают область плоскости O на всю плоскость XOY. Правда, это отображение не является взаимно однозначным (любой точке плоскости в плоскости XOY соответствует одна и та же точка (0;0)). Если взять область то (2) - взаимно однозначное отображение области на плоскость XOY с проколотым началом координат.