Накопленные частоты

Измеренные значения, мм	Частота	Накопленная частота	Накопленная относительная частота
1. 14,0 –14,1	1	1	0,01
2. 14,1 – 14,2	4	5	0,05
3. 14,2 – 14,3	4	9	0,09
4. 14,3 – 14,4	7	16	0,16
5. 14,4 – 14,5	16	32	0,32
6. 14,5 – 14,6	22	54	0,54
7. 14,6 – 14,7	18	72	0,72
8. 14,7 – 14,8	11	83	0,83
9. 14,8 – 14,9	8	91	0,91
10. 14,9 – 15,0	6	97	0,97
11. 15,0 – 15,1	2	99	0,99
12. 15,1 – 15,2	1	100	1,00

Если точки хорошо ложатся на прямую (см. рис. 7), то можно говорить о соответствии данных нормальному распределению.

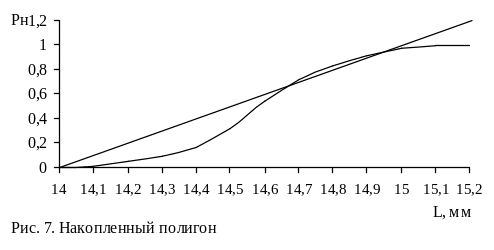
Рис. 7. Накопленный полигон

3. Диаграмма рассеяния и поле корреляции

Если сгруппировать данные в классы так, чтобы число значений x₁ было равно f₁, число значений x₂ = f_2,, а число значений x_k = y_k , то их сумма f₁ + f₂ + ... + f_k = N будет равна общему числу данных, для которых используются меры положения и меры разброса.

Величины, представляющие центр положения всех данных, называются мерами положения. Обычно используются среднее, медиана и мода.

Среднее значение определяется по формуле

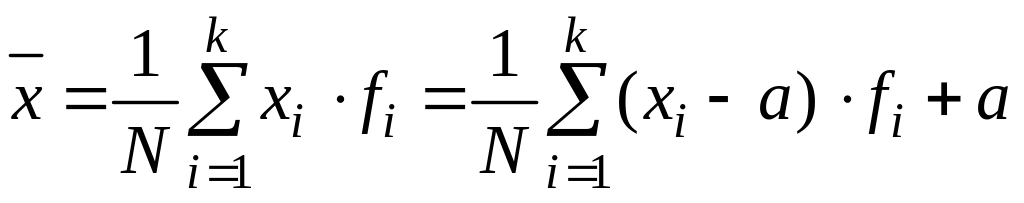, (5)

где a – произвольное число, называемое псевдосредним.

Медиана (серединная величина)  значение, которое окажется в самой середине ряда после упорядочения данных по возрастанию.

Мода  наиболее часто встречающееся значение среди всех данных.

Показатели, характеризующие степень разброса данных, называются мерами разброса. Обычно используется дисперсия, стандартное отклонение и размах.

Дисперсия определяется по формуле

. (6)

Среднеквадратичное стандартное отклонение

. (7)

Размах R равен разности максимального и минимального значений.

Коэффициент вариации равен отношению стандартного отключения и среднего значения:

. (8)

Для выявления силы связи корреляции между n парами данных для переменных x и y (x₁; y₁); (x₂; y₂);...; (x_n; y_n) эти данные наносятся на диаграмму рассеяния и для них вычисляется коэффициент корреляции по формуле

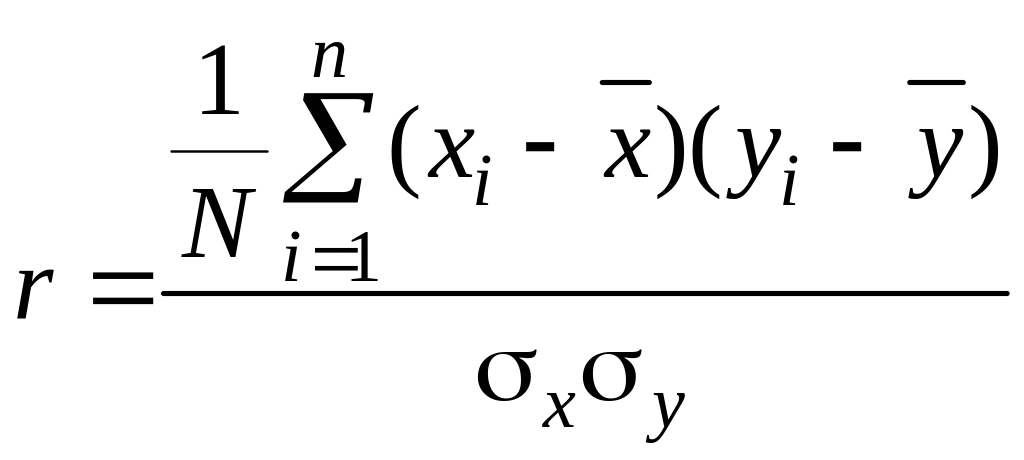, (9)

где _x, _y  стандартные отклонения x и y соответственно; n  число наблюдений; и  средние для x и y.

Для n пар данных (x₁; y₁); (x₂; y₂); ...; (x_n; y_n) зависимость между x и y

(10)

именуют регрессией.

Сила связи между случайными величинами x и y описывается диаграммой рассеяния (рис. 8), называемой еще полем корреляции.

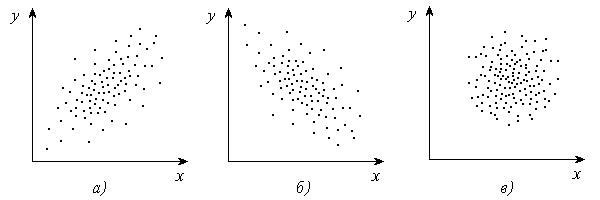
Рис. 8. Диаграммы рассеяния: положительная корреляция (а);

отрицательная корреляция (б); отсутствие корреляции (в)

Коэффициент корреляции всегда принимает значения 1< r <1.

При r > 0  корреляция положительная, при r < 0 корреляция отрицательная, а при r = 0 корреляции нет, т.е. между x и y нет линейной регрессионной зависимости.

Если рассмотреть смещение, например, (x₁; y₂); (x₂; y₃); ...; (x_n–1; y_n), то поле корреляции будет сдвинуто; подобный сдвиг именуется временным лагом. Методом наименьших квадратов определяют линейную зависимость Y = a + bx при различных временных лагах, рассчитывают коэффициенты корреляции и выбирают коэффициент с максимальным значением для определения времени сдвига рассматриваемой зависимости Y = F(X).