1 Билет.

1) Проекция силы на ось.

Проекцией силы F на ось Ox называется скалярная величина F_x, равная произведению ее модуля F на косинус угла между силой и положительным направлением оси:

F_x=F·cos  .

Проекция силы на ось:

положительна, если угол   -острый;

равна нулю, если угол   - прямой ( сила перпендикулярна оси );

отрицательна, если угол   - тупой.

2) Кручение, основные понятия.

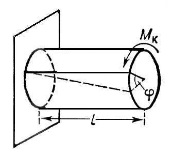Круче́ние - вид деформации, характеризующийся взаимным поворотом поперечных сечений стержня, вала и т. д. под влиянием моментов (пар сил), действующих в этих сечениях.

Х арактеризуется относительным углом закручивания θ:

 где G — модуль упругости при сдвиге; I_к и W_к — условный момент инерции и момент сопротивления при К.

3 . Определение текучести при растяжении.

Предел текучести – напряжение, при котором пластические деформации начинают интенсивно нарастать без заметного увеличения нагрузки.         

Условный предел текучести – напряжение, при котором остаточная пластическая деформация составляет 0,2%.

Билет 2.

1)Момент силы относительно точки.

Сила действ. на тв тело может охарактеризовать вращательный эффект. Колличе. мерой вращ. эффекта является момент силы относительно точки. МСОТ=произведению взятому с соответсвующим знаком величины системы на плечо(кратчайшее расстояение от выбранной точки до линии действия сил). Если сила стремится повернуть тв тело вокруг выбран. точки против часовой стрекли, то момент имеет +.

момент силы относительно точки в пространстве определим как век­торную вели­чину в виде векторного произведения , где  r - радиус-вектор, прове­дённый из точки O в точку приложения B силы F. Вектор  mo(F) нап­равлен перпендикулярно к плоскости, содержащей линию действия силы и точку О , так что с его конца вращение силы вокруг точки видно происходящим про­тив часовой стрелки. Модуль вектора mo(F)  равен произведению модуля силы на расстояние от данной точки до линии действия силы (плечо силы), т.е.

2) Рациональная форма сечения вала.

Тк в центре вала кас напряж-я малы то материал в центральной части существенно не нагружен и его практически без потери прочности можно удалить при этом вал станет существенно легче, а прочность существенно не уменьшится.

Вал кольцевой формы более рационален-легче и обладает тойже прочностью.

3) Предел пропорциональности при растяжении.

Наибольшее напряжение, при котором деформация прямо пропорцмональна нагрузке

δ_n=Fп/Ao

Условным пределом пропорциональности называется напряжение , при котором тангенс угла наклона касательной к диаграмме растяжения в 1.5 раза больше тангенса угла наклона линейного учаcтка этой диаграммы.

5 Билет.

1) Классификация внешних сил.

Внешние силы - силы взаимодействия между рассматриваемым элементом конструкции и связанными с ним телами. Внешние силы: 1)Объемные - равномерно распределены по всему объему материала и приложены в центре тяжести этого объема.

2)Поверхностные - приложены на поверхности материала, на малую площадь этой поверхности. (сила приложенная в точку)

Поверхностные силы:

1)Сосредоточенная сила

2)Распределенная нагрузка: а) равномерно распределенная по длине (Q); б)не равномерно 

3)По характеру действия делятся на: Статические, которые прикладываются к конструкции постепенно и в дальнейшем остаются постоянными. Динамические - нагрузки которые изменяются за малый промежуток времени.

2) Закон Гука при растяжении и сжатии.

Сила упругости, возникающая при деформации тела, пропорциональна удлинению этого тела. Нормальное напряжение s пропорционально относительному удлинению e

=E||

3. Векторное распределение момента силы относительно точки.

Момент силы относительно точки – векторное произведение радиус-вектора  точки  приложения силы на вектор силы. Mo(F) = r ⊗ F.

Вектор момента характеризует положение плоскости и направление вращательного действия силы, а также дает меру этого действия: 

|M₀(F)| = F⋅r⋅sinα = F⋅h,

Е сли сила F  задана своими проекциями Fx, Fy, Fz  на оси координат и даны координаты x, y, z  точки приложения этой силы, то момент силы относительно начала координат вычисляется следующим образом: