6) Магнитный поток. Теорема Гаусса для потока вектора .

Р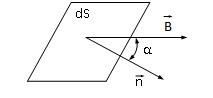 ассмотрим плоскую поверх-ть, имеющую бесконеч. малую площадь dS. Поверх-ть нах-ся в маг. поле.

Потоком вектора магн. индукции через эту поверх-ть или магнитным потоком назыв.

dФ = · 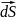, где · dS

В скаляр. форме:

dФ = B·cos · dS = · dS

где 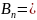B·cos - проекция вектора на направление нормали.

=

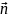
Магнитный поток через произвольную поверх-ть равен:Ф =

Если B = const и 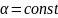, формула принимает вид:Ф = BS

[Ф] = 1Вб (вебер)

Рассмотрим маг. поток через бесконечно длинный соленоид, по кот. проходит ток 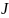. Маг. индукция однородного поля внутри соленоида равна:B = ,

где – относительная маг. проницаемость материала сердечника соленоида

Магнитный поток через 1 виток соленоида равен: = BS

Через витки:

Ѱ = = N = NBS =

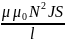
полный магнитный поток (потокосцепление)

Теорема Гаусса для потока вектора .

Поток вектора маг. индукции через любую замкнутую поверх-ть равен нулю.

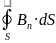= = 0

Этот результат явл-ся следствием замкнутости линий магнитной индукции.

7 Закон Ампера

Этот закон позволяет рассчитать силу, действующую на элемент dl проводника с током I находящегося в магнитном поле

dB=I[dl*B]

Направление силы Ампера можно найти по правилу левой руки: левую руку располагают там чтобы перпендикулярная к проводнику с током составляющая вектора магнитной индукции входила в ладонь,4 вытянутых пальца были направлены по направлению тока, тогда отогнутый под прямым углом большой палец покажет направление силы Ампера.

Fa

I

+ + в скалярной форме dF=IBLsina

a-угол между векторами B и dl

dl-вектор направление которого совпадает с направлением тока

+ + B

Проводник с током в магнитном поле

C

C’

F

L

. . . .

- . . . B

A

A’

I

dx

+ . . . .

Из Рисунка видно, что при перемещении проводника АС на бесконечно малое расстояние dx сила F совершит работу

dA=Fdx=IBLdx=IBds=IdФ

где dS=Ldx-площадь прямоуг. ACC’A

Работа по перемещению проводника с током в магнитном поле равна произведению силы тока магнитный поток, пересеченный движущимся проводником. В интегральной форме

A=I Ф

Работа по перемещению контура с током в магнитном поле

Можно рассчитать по формуле A=I Ф =I(Ф₂ –Ф₁ )

где Ф изменение магн. потока, сцепленного с контуром

Ф_2, Ф_{1 -} магн. Поток сцепленный с контуром в его конечном и начальном положении

8 Сила Лоренца - силу, действующую на движущуюся заряженную частицу со стороны магнитного поля, называют силой Лоренца

Силу Лоренца можно найти с помощью закона Ампера.

Модуль силы Лоренца равен отношению модуля силы F, действующей на участок проводника длиной 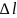 , к числу 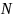  заряженных частиц, упорядоченно движущихся в этом участке проводника:

Рассмотрим отрезок тонкого прямого проводника с током. Пусть длина отрезка   и площадь поперечного сечения проводника 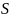  настолько малы, что вектор индукции магнитного поля  можно считать одинаковым в пределах этого отрезка проводника. Сила тока   в проводнике связана с зарядом частиц  , концентрацией заряженных частиц (числом зарядов в единице объема) и скоростью их упорядоченного движения   следующей формулой: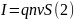

Модуль силы, действующей со стороны магнитного поля на выбранный элемент тока, равен: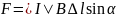

Подставляя в эту формулу выражение ( 2 ) для силы тока, получаем:

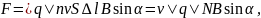
где 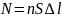— число заряженных частиц в рассматриваемом объеме. Следовательно, на каждый движущийся заряд со стороны магнитного поля действует сила Лоренца, равная:

г де α — угол между вектором скорости и вектором магнитной индукции. Направление силы Лоренца определяется с помощью правила левой руки,

Так как сила Лоренца перпендикулярна скорости частицы, то она не совершает работы. Под действием силы Лоренца меняется лишь направление скорости частицы.

Траектория движения заряженной частицы в однородном магнитном поле зависит от угла α между скоростью частицы и вектором магнитной индукции.

Заряженная частица, влетающая в однородное магнитное поле параллельно линиям магнитной индукции, движется вдоль этих линий. В этом случае α = 0 и соответственно Fл = 0

. В однородном магнитном поле частица, движущаяся перпендикулярно линиям индукции магнитного поля, под действием силы Лоренца приобретает центростремительное ускорение: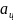 и движется по окружности.

При движении заряженной частицы в однородном электрическом поле радиус движения частицы остается неизменным:

Если угол   между первоначальным направлением скорости частицы и линиями магнитной индукции не равен ни 0°, ни 90°, ни 180°, траектория движения частицы представляет собой винтовую линию, накручивающуюся на линии магнитной индукции