
- •Програмування в середовищі Excel
- •79057, М. Львів, вул. Генерала Чупринки, 103/54
- •1. Формування рядка d:
- •2. Формування рядка d':
- •3. Сортування рядка d':
- •1. Формування рядка d:
- •2. Формування рядка d':
- •3. Сортування рядка d':
- •2. Формування рядка аr:
- •3. Формування рядка аRc:
- •4. Сортування рядка аRc:
- •2. Формування рядка аr:
- •3. Формування рядка аRc:
- •4. Сортування рядка аRc:
2. Формування рядка аr:
Клітини B149:F149 =ТРАНСП(B143:B147) – <Ctrl + Shift + Enter>
Клітини G149:K149 =ТРАНСП(C143:C147) – <Ctrl + Shift + Enter>
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Клітини V149:Z149 =ТРАНСП(F143:F147) – <Ctrl + Shift + Enter>
3. Формування рядка аRc:
Клітини B149:Z149 – <Ctrl + C> (де C – copy)
Клітина B151 – Правка, Специальная вставка... Вставить: значения <OK>
4. Сортування рядка аRc:
Клітини B151:Z151 Данные, Сортировка:
1. Сортировать по: убиванию
2. Идентифицировать поля по: отсутствует
3. Параметры
4. Сортировать по первому ключу: не производится
5. Сортировать: столбцы диапазона
6. <OK>
5. Формування матриці <А'>:
Клітини H143:H147 =ТРАНСП(B151:F151) – <Ctrl + Shift + Enter>
Клітини I143:I147 =ТРАНСП(G151:K151) – <Ctrl + Shift + Enter>
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Клітини L143:L147 =ТРАНСП(V151:Z151) – <Ctrl + Shift + Enter>
Тексти процедур і функцій – для середовища Visual Basic
' Сорт. рядків матриці у порядку зрост./спад. значень їх елементів
Sub Sort_rM(A, m, n)
Dim om() As Single
Dim i, j, ozn As Byte
ReDim om(1 To n)
ozn =Application.InputBox("Введіть ознаку сортування: 1 - за спаданням; 2 - за зростанням")
For i =1 To m
For j =1 To n: om(j) =A(i, j): Next j
If ozn =1 Then ' Сорт. масиву за спаданням
'Сортування одновимірного масиву методом перестановок
Call Sort_P(om, n)
Else ' Сорт. масиву за зростанням
' Сортування одновимірного масиву методом пошуку найменшого елемента
Call Sort_M(om, n)
End If
For j =1 To n: A(i, j) =om(j): Next j
Next i
End Sub
' Сорт. стовпців матриці у порядку зрост./спад. значень їх елементів
Sub Sort_sM(A, m, n)
Dim om() As Single
Dim i, j, ozn As Byte
ReDim om(1 To m)
ozn =Application.InputBox("Введіть ознаку сортування: 1 - за спаданням; 2 - за зростанням")
For j =1 To n
For i =1 To m: om(i) =A(i, j): Next i
If ozn =1 Then ' Сорт. масиву за спаданням
' Сортування одновимірного масиву методом перестановок
Call Sort_P(om, m)
Else ' Сорт. масиву за зростанням
' Сортування одновимірного масиву методом пошуку найменшого елемента
Call Sort_M(om, m)
End If
For i =1 To n: A(i, j) =om(i): Next i
Next j
End Sub
' Сорт. матриці по рядках у порядку зрост./спад. значень їх елементів
Sub Sort_Mr(A, m, n)
Dim om() As Single
Dim i, j, ozn As Byte
ReDim om(1 To m * n)
ozn =Application.InputBox("Введіть ознаку сортування: 1 - за спаданням; 2 - за зростанням")
For i =1 To m
For j =1 To n: om((i - 1) * n + j) =A(i, j): Next j
Next i
If ozn =1 Then ' Сорт. масиву за спаданням
' Сортування одновимірного масиву методом перестановок
Call Sort_P(om, m * n)
Else ' Сорт. масиву за зростанням
' Сортування одновимірного масиву методом пошуку найменшого елемента
Call Sort_M(om, m * n)
End If
For i =1 To m
For j =1 To n: A(i, j) =om((i - 1) * n + j): Next j
Next i
End Sub
' Сорт. матриці по стовпцях у порядку зрост./спад. значень їх елементів
Sub Sort_Ms(A, m, n)
Dim om() As Single
Dim i, j, ozn As Byte
ReDim om(1 To m * n)
ozn =Application.InputBox("Введіть ознаку сортування: 1 - за спаданням; 2 - за зростанням")
For j =1 To n
For i =1 To m: om((j - 1) * m + i) =A(i, j): Next i
Next j
If ozn =1 Then ' Сорт. масиву за спаданням
' Сортування одновимірного масиву методом перестановок
Call Sort_P(om, m * n)
Else ' Сорт. масиву за зростанням
' Сортування одновимірного масиву методом пошуку найменшого елемента
Call Sort_M(om, m * n)
End If
For j =1 To n
For i =1 To m: A(i, j) =om((j - 1) * m + i): Next i
Next j
End Sub
Sub Zavd_6_2() 'Сортування елементів матриць
Dim i, j As Byte
Dim row, col, Oz_s As Byte
Dim A_mas()As Single
Set myCELL =Application.InputBox( _
prompt:="Виберіть вхідну матрицю даних (без заголовка)", _
Type:=8)
Set myCELL2 =Application.InputBox( _
prompt:="Виберіть клітинку, з якої будуть виводитися результати розрахунку", _
Type:=8)
Oz_s =Application.InputBox("Введіть ознаку сортування: 1 - рядків; 2 - стовпців; 3 - по рядках; 4 - по стовпцях")
row =myCELL.Rows.Count 'Обчислення кількості рядків
col =myCELL.Columns.Count 'Обчислення кількості стовпців
ReDim A_mas(1 To row, 1 To col)
' Занесення введених елементів у двовимірний масив
For i =1 To row
For j =1 To col
A_mas(i, j) =myCELL.Columns(j).Cells(i)
Next j
Next i
Select Case Oz_s ' Вибір потрібного номера.
Case 1 ' Сорт. рядків матриці у порядку зрост./спад. значень їх елементів
Call Sort_rM(A_mas, row, col)
Case 2 ' Сорт. стовпців матриці у порядку зрост./спад. значень їх елементів
Call Sort_sM(A_mas, row, col)
Case 3 ' Сорт. матриці по рядках у порядку зрост./спад. значень їх елементів
Call Sort_Mr(A_mas, row, col)
Case 4 ' Сорт. матриці по стовпцях у порядку зрост./спад. значень їх елементів
Call Sort_Ms(A_mas, row, col)
End Select
' Виведених елементів двовимірного масиву
For i =1 To row
For j =1 To col
myCELL2.Offset(i - 1, j - 1).Value =A_mas(i, j)
Next j
Next i
myCELL2.Offset(row, 0).Value ="Кінець розрахунку"
End Sub
Задача 6.3. Відповідно до номера варіанту (прикл. 1 і 2) у середовищі Excel скласти програму для інвертування елементів вектора-рядка/стовпця і матриці, а саме:
інвертування елементів рядка
 ;
;інвертування елементів стовпця
 ;
;інвертування елементів матриці по стовпцях;
інвертування елементів матриці по рядках;
інвертування елементів матриці по стовпцях і по рядках;
інвертування елементів матриці по рядках і по стовпцях.
Інвертування елементів одновимірного масиву
Інвертування елементів рядка
|
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
164 |
|
|
|
|
|
|
В' |
|
|
|
|
|
|
|
|
|
|
165 |
D |
|
|
|
|
|
0 |
0 |
0 |
0 |
1 |
|
Dir |
|
|
|
|
166 |
1,08 |
-4,91 |
31,34 |
324,23 |
2365,17 |
* |
0 |
0 |
0 |
1 |
0 |
= |
2365,17 |
324,23 |
31,34 |
-4,91 |
1,08 |
167 |
|
|
|
|
|
|
0 |
0 |
1 |
0 |
0 |
|
|
|
|
|
|
168 |
|
|
|
|
|
|
0 |
1 |
0 |
0 |
0 |
|
|
|
|
|
|
169 |
|
|
|
|
|
|
1 |
0 |
0 |
0 |
0 |
|
|
|
|
|
|
Клітини B166:F166 =E14 – <Ctrl + Enter>
Клітини N166:R166 =МУМНОЖ(B166:F166;H165:L169) – <Ctrl + Shift + Enter>
Інвертування елементів стовпця
|
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
171 |
В' |
|
|
|
|
|
D |
|
Dis |
|
|
|
|
|
|
|
|
172 |
0 |
0 |
0 |
0 |
1 |
|
1,08 |
|
2365,17 |
|
|
|
|
|
|
|
|
173 |
0 |
0 |
0 |
1 |
0 |
* |
-4,91 |
= |
324,23 |
|
|
|
|
|
|
|
|
174 |
0 |
0 |
1 |
0 |
0 |
|
31,34 |
|
31,34 |
|
|
|
|
|
|
|
|
175 |
0 |
1 |
0 |
0 |
0 |
|
324,23 |
|
-4,91 |
|
|
|
|
|
|
|
|
176 |
1 |
0 |
0 |
0 |
0 |
|
2365,17 |
|
1,08 |
|
|
|
|
|
|
|
|
Клітини H172:H176 =C14 – <Ctrl + Enter>
Клітини J172:J176 =МУМНОЖ(B172:F176;H172:H176) – <Ctrl + Shift + Enter>
Інвертування елементів двовимірного масиву
Інвертування матриці по стовпцях
|
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
181 |
A |
|
|
|
|
|
В' |
|
|
|
|
|
Ais |
|
|
|
|
182 |
0,10 |
8,11 |
40,44 |
65,52 |
57,51 |
|
0 |
0 |
0 |
0 |
1 |
|
57,51 |
65,52 |
40,44 |
8,11 |
0,10 |
183 |
1,20 |
2,97 |
6,75 |
12,61 |
14,10 |
* |
0 |
0 |
0 |
1 |
0 |
= |
14,10 |
12,61 |
6,75 |
2,97 |
1,20 |
184 |
1,29 |
11,08 |
47,19 |
78,13 |
71,61 |
|
0 |
0 |
1 |
0 |
0 |
|
71,61 |
78,13 |
47,19 |
11,08 |
1,29 |
185 |
2,49 |
14,05 |
53,95 |
90,75 |
85,70 |
|
0 |
1 |
0 |
0 |
0 |
|
85,70 |
90,75 |
53,95 |
14,05 |
2,49 |
186 |
3,79 |
25,13 |
101,14 |
168,88 |
157,31 |
|
1 |
0 |
0 |
0 |
0 |
|
157,31 |
168,88 |
101,14 |
25,13 |
3,79 |
Клітини B182:F186 =C48 – <Ctrl + Enter>
Клітини J172:J176 =МУМНОЖ(B182:F186;H182:L186) – <Ctrl + Shift + Enter>
Інвертування матриці по рядках
|
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
189 |
В' |
|
|
|
|
|
A |
|
|
|
|
|
Air |
|
|
|
|
190 |
0 |
0 |
0 |
0 |
1 |
|
0,10 |
8,11 |
40,44 |
65,52 |
57,51 |
|
3,786 |
25,135 |
101,141 |
168,884 |
157,311 |
191 |
0 |
0 |
0 |
1 |
0 |
* |
1,20 |
2,97 |
6,75 |
12,61 |
14,10 |
= |
2,492 |
14,053 |
53,946 |
90,750 |
85,704 |
192 |
0 |
0 |
1 |
0 |
0 |
|
1,29 |
11,08 |
47,19 |
78,13 |
71,61 |
|
1,294 |
11,082 |
47,194 |
78,135 |
71,607 |
193 |
0 |
1 |
0 |
0 |
0 |
|
2,49 |
14,05 |
53,95 |
90,75 |
85,70 |
|
1,198 |
2,970 |
6,752 |
12,615 |
14,097 |
194 |
1 |
0 |
0 |
0 |
0 |
|
3,79 |
25,13 |
101,14 |
168,88 |
157,31 |
|
0,096 |
8,112 |
40,443 |
65,520 |
57,510 |
Клітини B190:F194 =C48 – <Ctrl + Enter>
Клітини N190:R194 =МУМНОЖ(B190:F194;H190:L194) – <Ctrl + Shift + Enter>
Інвертування матриці по стовпцях і по рядках
|
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
197 |
A |
|
|
|
|
|
В' |
|
|
|
|
|
Ais |
|
|
|
|
198 |
0,10 |
8,11 |
40,44 |
65,52 |
57,51 |
|
0 |
0 |
0 |
0 |
1 |
|
57,51 |
65,52 |
40,44 |
8,11 |
0,10 |
199 |
1,20 |
2,97 |
6,75 |
12,61 |
14,10 |
* |
0 |
0 |
0 |
1 |
0 |
= |
14,10 |
12,61 |
6,75 |
2,97 |
1,20 |
200 |
1,29 |
11,08 |
47,19 |
78,13 |
71,61 |
|
0 |
0 |
1 |
0 |
0 |
|
71,61 |
78,13 |
47,19 |
11,08 |
1,29 |
201 |
2,49 |
14,05 |
53,95 |
90,75 |
85,70 |
|
0 |
1 |
0 |
0 |
0 |
|
85,70 |
90,75 |
53,95 |
14,05 |
2,49 |
202 |
3,79 |
25,13 |
101,14 |
168,88 |
157,31 |
|
1 |
0 |
0 |
0 |
0 |
|
157,31 |
168,88 |
101,14 |
25,13 |
3,79 |
203 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
204 |
В' |
|
|
|
|
|
Ais |
|
|
|
|
|
Aisr |
|
|
|
|
205 |
0 |
0 |
0 |
0 |
1 |
|
57,51 |
65,52 |
40,44 |
8,11 |
0,10 |
|
157,31 |
168,88 |
101,14 |
25,13 |
3,79 |
206 |
0 |
0 |
0 |
1 |
0 |
* |
14,10 |
12,61 |
6,75 |
2,97 |
1,20 |
= |
85,70 |
90,75 |
53,95 |
14,05 |
2,49 |
207 |
0 |
0 |
1 |
0 |
0 |
|
71,61 |
78,13 |
47,19 |
11,08 |
1,29 |
|
71,61 |
78,13 |
47,19 |
11,08 |
1,29 |
208 |
0 |
1 |
0 |
0 |
0 |
|
85,70 |
90,75 |
53,95 |
14,05 |
2,49 |
|
14,10 |
12,61 |
6,75 |
2,97 |
1,20 |
209 |
1 |
0 |
0 |
0 |
0 |
|
157,31 |
168,88 |
101,14 |
25,13 |
3,79 |
|
57,51 |
65,52 |
40,44 |
8,11 |
0,10 |
Клітини B198:F202 =C48 – <Ctrl + Enter>
Клітини N198:R202 =МУМНОЖ(B198:F202;H198:L202) – <Ctrl + Shift + Enter>
Клітини H205:L209 =N198 – <Ctrl + Enter>
Клітини N205:R209 =МУМНОЖ(B205:F209;H205:L209) – <Ctrl + Shift + Enter>
Інвертування матриці по рядках і стовпцях
|
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
212 |
В' |
|
|
|
|
|
A |
|
|
|
|
|
Air |
|
|
|
|
213 |
0 |
0 |
0 |
0 |
1 |
|
0,10 |
8,11 |
40,44 |
65,52 |
57,51 |
|
3,79 |
25,13 |
101,14 |
168,88 |
157,31 |
214 |
0 |
0 |
0 |
1 |
0 |
* |
1,20 |
2,97 |
6,75 |
12,61 |
14,10 |
= |
2,49 |
14,05 |
53,95 |
90,75 |
85,70 |
215 |
0 |
0 |
1 |
0 |
0 |
|
1,29 |
11,08 |
47,19 |
78,13 |
71,61 |
|
1,29 |
11,08 |
47,19 |
78,13 |
71,61 |
216 |
0 |
1 |
0 |
0 |
0 |
|
2,49 |
14,05 |
53,95 |
90,75 |
85,70 |
|
1,20 |
2,97 |
6,75 |
12,61 |
14,10 |
217 |
1 |
0 |
0 |
0 |
0 |
|
3,79 |
25,13 |
101,14 |
168,88 |
157,31 |
|
0,10 |
8,11 |
40,44 |
65,52 |
57,51 |
218 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
219 |
Air |
|
|
|
|
|
В' |
|
|
|
|
|
Airs |
|
|
|
|
220 |
3,79 |
25,13 |
101,14 |
168,88 |
157,31 |
|
0 |
0 |
0 |
0 |
1 |
|
157,31 |
168,88 |
101,14 |
25,13 |
3,79 |
221 |
2,49 |
14,05 |
53,95 |
90,75 |
85,70 |
* |
0 |
0 |
0 |
1 |
0 |
= |
85,70 |
90,75 |
53,95 |
14,05 |
2,49 |
222 |
1,29 |
11,08 |
47,19 |
78,13 |
71,61 |
|
0 |
0 |
1 |
0 |
0 |
|
71,61 |
78,13 |
47,19 |
11,08 |
1,29 |
223 |
1,20 |
2,97 |
6,75 |
12,61 |
14,10 |
|
0 |
1 |
0 |
0 |
0 |
|
14,10 |
12,61 |
6,75 |
2,97 |
1,20 |
224 |
0,10 |
8,11 |
40,44 |
65,52 |
57,51 |
|
1 |
0 |
0 |
0 |
0 |
|
57,51 |
65,52 |
40,44 |
8,11 |
0,10 |
Клітини H213:L217 =C48 – <Ctrl + Enter>
Клітини N213:R217 =МУМНОЖ(B213:F217;H213:L217) – <Ctrl + Shift + Enter>
Клітини B220:F224 =N213 – <Ctrl + Enter>
Клітини N220:R224 =МУМНОЖ(B220:F224;H220:L224) – <Ctrl + Shift + Enter>
Задача 6.4. Відповідно до номера варіанту (прикл. 1 і 2) у середовищі Excel скласти програму для перестановки елементів вектора-рядка/стовпця і матриці, а саме:
перестановка елементів рядка – останнього з передостаннім;
перестановка елементів рядка – другого з останнім;
перестановка елементів стовпця – останнього з передостаннім;
перестановка елементів стовпця – другого з останнім;
перестановка стовпців матриці – останнього з передостаннім;
перестановка стовпців матриці – другого з останнім;
перестановка рядків матриці – останнього з передостаннім;
перестановка рядків матриці – другого з останнім.
Перестановка елементів одновимірного масиву
Перестановка елементів рядка
|
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
230 |
|
|
|
|
|
|
P5,4 |
|
|
|
|
|
|
|
|
|
|
231 |
D |
|
|
|
|
|
1 |
0 |
0 |
0 |
0 |
|
D4,5 |
|
|
|
|
232 |
1,08 |
-4,91 |
31,34 |
324,23 |
2365,17 |
* |
0 |
1 |
0 |
0 |
0 |
= |
1,08 |
-4,91 |
31,34 |
2365,17 |
324,23 |
233 |
|
|
|
|
|
|
0 |
0 |
1 |
0 |
0 |
|
|
|
|
|
|
234 |
|
|
|
|
|
|
0 |
0 |
0 |
0 |
1 |
|
|
|
|
|
|
235 |
|
|
|
|
|
|
0 |
0 |
0 |
1 |
0 |
|
|
|
|
|
|
236 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
237 |
|
|
|
|
|
|
P5,2 |
|
|
|
|
|
|
|
|
|
|
238 |
D |
|
|
|
|
|
1 |
0 |
0 |
0 |
0 |
|
D2,5 |
|
|
|
|
239 |
1,08 |
-4,91 |
31,34 |
324,23 |
2365,17 |
* |
0 |
0 |
0 |
0 |
1 |
= |
1,08 |
2365,17 |
31,34 |
324,23 |
-4,91 |
240 |
|
|
|
|
|
|
0 |
0 |
1 |
0 |
0 |
|
|
|
|
|
|
241 |
|
|
|
|
|
|
0 |
0 |
0 |
1 |
0 |
|
|
|
|
|
|
242 |
|
|
|
|
|
|
0 |
1 |
0 |
0 |
0 |
|
|
|
|
|
|
Клітини B232:F232 =E14 – <Ctrl + Enter>
Клітини N232:R232 =МУМНОЖ(B232:F232;H231:L235) – <Ctrl + Shift + Enter>
Клітини B239:F239 =E14 – <Ctrl + Enter>
Клітини N239:R239 =МУМНОЖ(B239:F239;H238:L242) – <Ctrl + Shift + Enter>
Перестановка елементів стовпця
|
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
246 |
P5,4 |
|
|
|
|
|
D |
|
D4,5 |
|
|
|
|
|
|
|
|
247 |
1 |
0 |
0 |
0 |
0 |
|
1,08 |
|
1,08 |
|
|
|
|
|
|
|
|
248 |
0 |
1 |
0 |
0 |
0 |
* |
-4,91 |
= |
-4,91 |
|
|
|
|
|
|
|
|
249 |
0 |
0 |
1 |
0 |
0 |
|
31,34 |
|
31,34 |
|
|
|
|
|
|
|
|
250 |
0 |
0 |
0 |
0 |
1 |
|
324,23 |
|
2365,17 |
|
|
|
|
|
|
|
|
251 |
0 |
0 |
0 |
1 |
0 |
|
2365,17 |
|
324,23 |
|
|
|
|
|
|
|
|
252 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
253 |
P5,2 |
|
|
|
|
|
D |
|
D2,5 |
|
|
|
|
|
|
|
|
254 |
1 |
0 |
0 |
0 |
0 |
|
1,08 |
|
1,08 |
|
|
|
|
|
|
|
|
255 |
0 |
0 |
0 |
0 |
1 |
* |
-4,91 |
= |
2365,17 |
|
|
|
|
|
|
|
|
256 |
0 |
0 |
1 |
0 |
0 |
|
31,34 |
|
31,34 |
|
|
|
|
|
|
|
|
257 |
0 |
0 |
0 |
1 |
0 |
|
324,23 |
|
324,23 |
|
|
|
|
|
|
|
|
258 |
0 |
1 |
0 |
0 |
0 |
|
2365,17 |
|
-4,91 |
|
|
|
|
|
|
|
|
Клітини H247:H251 =C14 – <Ctrl + Enter>
Клітини J247:J251 =МУМНОЖ(B247:F251;H247:H251) – <Ctrl + Shift + Enter>
Клітини H254:H258 =C14 – <Ctrl + Enter>
Клітини J254:J258 =МУМНОЖ(B254:F258;H254:H258) – <Ctrl + Shift + Enter>
Перестановка елементів двовимірного масиву
Перестановка стовпців матриці
|
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
262 |
A |
|
|
|
|
|
P5,4 |
|
|
|
|
|
D4,5 |
|
|
|
|
263 |
0,10 |
8,11 |
40,44 |
65,52 |
57,51 |
|
1 |
0 |
0 |
0 |
0 |
|
0,10 |
8,11 |
40,44 |
57,51 |
65,52 |
264 |
1,20 |
2,97 |
6,75 |
12,61 |
14,10 |
x |
0 |
1 |
0 |
0 |
0 |
= |
1,20 |
2,97 |
6,75 |
14,10 |
12,61 |
265 |
1,29 |
11,08 |
47,19 |
78,13 |
71,61 |
|
0 |
0 |
1 |
0 |
0 |
|
1,29 |
11,08 |
47,19 |
71,61 |
78,13 |
266 |
2,49 |
14,05 |
53,95 |
90,75 |
85,70 |
|
0 |
0 |
0 |
0 |
1 |
|
2,49 |
14,05 |
53,95 |
85,70 |
90,75 |
267 |
3,79 |
25,13 |
101,14 |
168,88 |
157,31 |
|
0 |
0 |
0 |
1 |
0 |
|
3,79 |
25,13 |
101,14 |
157,31 |
168,88 |
268 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
269 |
A |
|
|
|
|
|
P5,2 |
|
|
|
|
|
D2,5 |
|
|
|
|
270 |
0,10 |
8,11 |
40,44 |
65,52 |
57,51 |
|
1 |
0 |
0 |
0 |
0 |
|
0,10 |
57,51 |
40,44 |
65,52 |
8,11 |
271 |
1,20 |
2,97 |
6,75 |
12,61 |
14,10 |
x |
0 |
0 |
0 |
0 |
1 |
= |
1,20 |
14,10 |
6,75 |
12,61 |
2,97 |
272 |
1,29 |
11,08 |
47,19 |
78,13 |
71,61 |
|
0 |
0 |
1 |
0 |
0 |
|
1,29 |
71,61 |
47,19 |
78,13 |
11,08 |
273 |
2,49 |
14,05 |
53,95 |
90,75 |
85,70 |
|
0 |
0 |
0 |
1 |
0 |
|
2,49 |
85,70 |
53,95 |
90,75 |
14,05 |
274 |
3,79 |
25,13 |
101,14 |
168,88 |
157,31 |
|
0 |
1 |
0 |
0 |
0 |
|
3,79 |
157,31 |
101,14 |
168,88 |
25,13 |
Клітини B263:F267 =C48 – <Ctrl + Enter>
Клітини N263:R267 =МУМНОЖ(B263:F267;H263:L267) – <Ctrl + Shift + Enter>
Клітини B270:F274 =C48 – <Ctrl + Enter>
Клітини N270:R274 =МУМНОЖ(B270:F274;H270:L274) – <Ctrl + Shift + Enter>
Перестановка рядків матриці
|
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
278 |
P5,4 |
|
|
|
|
|
A |
|
|
|
|
|
4,5D |
|
|
|
|
279 |
1 |
0 |
0 |
0 |
0 |
|
0,10 |
8,11 |
40,44 |
65,52 |
57,51 |
|
0,10 |
8,11 |
40,44 |
65,52 |
57,51 |
280 |
0 |
1 |
0 |
0 |
0 |
x |
1,20 |
2,97 |
6,75 |
12,61 |
14,10 |
= |
1,20 |
2,97 |
6,75 |
12,61 |
14,10 |
281 |
0 |
0 |
1 |
0 |
0 |
|
1,29 |
11,08 |
47,19 |
78,13 |
71,61 |
|
1,29 |
11,08 |
47,19 |
78,13 |
71,61 |
282 |
0 |
0 |
0 |
0 |
1 |
|
2,49 |
14,05 |
53,95 |
90,75 |
85,70 |
|
3,79 |
25,13 |
101,14 |
168,88 |
157,31 |
283 |
0 |
0 |
0 |
1 |
0 |
|
3,79 |
25,13 |
101,14 |
168,88 |
157,31 |
|
2,49 |
14,05 |
53,95 |
90,75 |
85,70 |
284 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
285 |
P5,2 |
|
|
|
|
|
A |
|
|
|
|
|
2,5D |
|
|
|
|
286 |
1 |
0 |
0 |
0 |
0 |
|
0,10 |
8,11 |
40,44 |
65,52 |
57,51 |
|
0,10 |
8,11 |
40,44 |
65,52 |
57,51 |
287 |
0 |
0 |
0 |
0 |
1 |
x |
1,20 |
2,97 |
6,75 |
12,61 |
14,10 |
= |
3,79 |
25,13 |
101,14 |
168,88 |
157,31 |
288 |
0 |
0 |
1 |
0 |
0 |
|
1,29 |
11,08 |
47,19 |
78,13 |
71,61 |
|
1,29 |
11,08 |
47,19 |
78,13 |
71,61 |
289 |
0 |
0 |
0 |
1 |
0 |
|
2,49 |
14,05 |
53,95 |
90,75 |
85,70 |
|
2,49 |
14,05 |
53,95 |
90,75 |
85,70 |
290 |
0 |
1 |
0 |
0 |
0 |
|
3,79 |
25,13 |
101,14 |
168,88 |
157,31 |
|
1,20 |
2,97 |
6,75 |
12,61 |
14,10 |
Клітини H279:L283 =C48 – <Ctrl + Enter>
Клітини N279:R283 =МУМНОЖ(B279:F283;H279:L283) – <Ctrl + Shift + Enter>
Клітини H286:L290 =C48 – <Ctrl + Enter>
Клітини N286:R290 =МУМНОЖ(B286:F290;H286:L290) – <Ctrl + Shift + Enter>
Задача 6.5. Відповідно до номера варіанту (прикл. 1 і 2) у середовищі Excel скласти програму для виконання зсуву елементів вектора-рядка/стовпця і матриці, а саме:
зсув елементів рядка – на одну позицію вправо;
зсув елементів рядка – на дві позиції вправо;
зсув елементів рядка – на одну позицію вліво;
зсув елементів рядка – на дві позиції вліво;
зсув елементів стовпця – на одну позицію вверх;
зсув елементів стовпця – на дві позиції вверх;
зсув елементів стовпця – на одну позицію вниз;
зсув елементів стовпця – на дві позиції вниз;
зсув стовпців матриці – на один стовпець вправо;
зсув стовпців матриці – на два стовпці вправо;
зсув стовпців матриці – на один стовпець вліво;
зсув стовпців матриці – на два стовпці вліво;
зсув рядків матриці – на один рядок вверх;
зсув рядків матриці – на два рядки вверх;
зсув рядків матриці
 – на один рядок вниз;
– на один рядок вниз;зсув рядків матриці – на два рядки вниз.
Зсув елементів одновимірного масиву
Зсув елементів рядка
|
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
297 |
На 1-у позицію вправо |
|
Z1 |
|
|
|
|
|
|
|
|
|
|
||||
298 |
D |
--> |
|
|
|
|
0 |
1 |
0 |
0 |
0 |
|
Dz1 |
|
|
|
|
299 |
1,08 |
-4,91 |
31,34 |
324,23 |
2365,17 |
* |
0 |
0 |
1 |
0 |
0 |
= |
2365,17 |
1,08 |
-4,91 |
31,34 |
324,23 |
300 |
|
|
|
|
|
|
0 |
0 |
0 |
1 |
0 |
|
|
|
|
|
|
301 |
|
|
|
|
|
|
0 |
0 |
0 |
0 |
1 |
|
|
|
|
|
|
302 |
|
|
|
|
|
|
1 |
0 |
0 |
0 |
0 |
|
|
|
|
|
|
303 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
304 |
На 2-і позиції вправо |
|
Z2 |
|
|
|
|
|
|
|
|
|
|
||||
305 |
D |
--> |
|
|
|
|
0 |
0 |
1 |
0 |
0 |
|
Dz2 |
|
|
|
|
306 |
1,08 |
-4,91 |
31,34 |
324,23 |
2365,17 |
* |
0 |
0 |
0 |
1 |
0 |
= |
324,23 |
2365,17 |
1,08 |
-4,91 |
31,34 |
307 |
|
|
|
|
|
|
0 |
0 |
0 |
0 |
1 |
|
|
|
|
|
|
308 |
|
|
|
|
|
|
1 |
0 |
0 |
0 |
0 |
|
|
|
|
|
|
309 |
|
|
|
|
|
|
0 |
1 |
0 |
0 |
0 |
|
|
|
|
|
|
310 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
311 |
На 1-у позицію вліво |
|
1Z |
|
|
|
|
|
|
|
|
|
|
||||
312 |
D |
<-- |
|
|
|
|
0 |
0 |
0 |
0 |
1 |
|
z1D |
|
|
|
|
313 |
1,08 |
-4,91 |
31,34 |
324,23 |
2365,17 |
* |
1 |
0 |
0 |
0 |
0 |
= |
-4,91 |
31,34 |
324,23 |
2365,17 |
1,08 |
314 |
|
|
|
|
|
|
0 |
1 |
0 |
0 |
0 |
|
|
|
|
|
|
315 |
|
|
|
|
|
|
0 |
0 |
1 |
0 |
0 |
|
|
|
|
|
|
316 |
|
|
|
|
|
|
0 |
0 |
0 |
1 |
0 |
|
|
|
|
|
|
317 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
318 |
На 2-у позицію вліво |
|
2Z |
|
|
|
|
|
|
|
|
|
|
||||
319 |
D |
<-- |
|
|
|
|
0 |
0 |
0 |
1 |
0 |
|
z1D |
|
|
|
|
320 |
1,08 |
-4,91 |
31,34 |
324,23 |
2365,17 |
* |
0 |
0 |
0 |
0 |
1 |
= |
31,34 |
324,23 |
2365,17 |
1,08 |
-4,91 |
321 |
|
|
|
|
|
|
1 |
0 |
0 |
0 |
0 |
|
|
|
|
|
|
322 |
|
|
|
|
|
|
0 |
1 |
0 |
0 |
0 |
|
|
|
|
|
|
323 |
|
|
|
|
|
|
0 |
0 |
1 |
0 |
0 |
|
|
|
|
|
|
Клітини B299:F299 =E14 – <Ctrl + Enter>
Клітини N299:R299 =МУМНОЖ(B299:F299;H298:L302) – <Ctrl + Shift + Enter>
Клітини B306:F306 =E14 – <Ctrl + Enter>
Клітини N306:R306 =МУМНОЖ(B306:F306;H305:L309) – <Ctrl + Shift + Enter>
Клітини B313:F313 =E14 – <Ctrl + Enter>
Клітини N313:R313 =МУМНОЖ(B313:F313;H312:L316) – <Ctrl + Shift + Enter>
Клітини B320:F320 =E14 – <Ctrl + Enter>
Клітини N320:R320 =МУМНОЖ(B320:F320;H319:L323) – <Ctrl + Shift + Enter>
Зсув елементів стовпця
|
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
327 |
На 1-у позицію вверх |
|
|
|
|
|
|
|
|
|
|
|
|
||||
328 |
Z1 |
|
|
|
|
|
D |
|
Dz1 |
|
|
|
|
|
|
|
|
329 |
0 |
1 |
0 |
0 |
0 |
|
1,08 |
|
-4,91 |
|
|
|
|
|
|
|
|
330 |
0 |
0 |
1 |
0 |
0 |
* |
-4,91 |
= |
31,34 |
|
|
|
|
|
|
|
|
331 |
0 |
0 |
0 |
1 |
0 |
|
31,34 |
|
324,23 |
|
|
|
|
|
|
|
|
332 |
0 |
0 |
0 |
0 |
1 |
|
324,23 |
|
2365,17 |
|
|
|
|
|
|
|
|
333 |
1 |
0 |
0 |
0 |
0 |
|
2365,17 |
|
1,08 |
|
|
|
|
|
|
|
|
334 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
335 |
На 2-і позиції вверх |
|
|
|
|
|
|
|
|
|
|
|
|
||||
336 |
Z2 |
|
|
|
|
|
D |
|
Dz2 |
|
|
|
|
|
|
|
|
337 |
0 |
0 |
1 |
0 |
0 |
|
1,08 |
|
31,34 |
|
|
|
|
|
|
|
|
338 |
0 |
0 |
0 |
1 |
0 |
* |
-4,91 |
= |
324,23 |
|
|
|
|
|
|
|
|
339 |
0 |
0 |
0 |
0 |
1 |
|
31,34 |
|
2365,17 |
|
|
|
|
|
|
|
|
340 |
1 |
0 |
0 |
0 |
0 |
|
324,23 |
|
1,08 |
|
|
|
|
|
|
|
|
341 |
0 |
1 |
0 |
0 |
0 |
|
2365,17 |
|
-4,91 |
|
|
|
|
|
|
|
|
342 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
343 |
На 1-у позицію вниз |
|
|
|
|
|
|
|
|
|
|
|
|
||||
344 |
1Z |
|
|
|
|
|
D |
|
Dz1 |
|
|
|
|
|
|
|
|
345 |
0 |
0 |
0 |
0 |
1 |
|
1,08 |
|
2365,17 |
|
|
|
|
|
|
|
|
346 |
1 |
0 |
0 |
0 |
0 |
* |
-4,91 |
= |
1,08 |
|
|
|
|
|
|
|
|
347 |
0 |
1 |
0 |
0 |
0 |
|
31,34 |
|
-4,91 |
|
|
|
|
|
|
|
|
348 |
0 |
0 |
1 |
0 |
0 |
|
324,23 |
|
31,34 |
|
|
|
|
|
|
|
|
349 |
0 |
0 |
0 |
1 |
0 |
|
2365,17 |
|
324,23 |
|
|
|
|
|
|
|
|
350 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
351 |
На 2-i позиції вниз |
|
|
|
|
|
|
|
|
|
|
|
|
||||
352 |
2Z |
|
|
|
|
|
D |
|
Dz2 |
|
|
|
|
|
|
|
|
353 |
0 |
0 |
0 |
1 |
0 |
|
1,08 |
|
324,23 |
|
|
|
|
|
|
|
|
354 |
0 |
0 |
0 |
0 |
1 |
* |
-4,91 |
= |
2365,17 |
|
|
|
|
|
|
|
|
355 |
1 |
0 |
0 |
0 |
0 |
|
31,34 |
|
1,08 |
|
|
|
|
|
|
|
|
356 |
0 |
1 |
0 |
0 |
0 |
|
324,23 |
|
-4,91 |
|
|
|
|
|
|
|
|
357 |
0 |
0 |
1 |
0 |
0 |
|
2365,17 |
|
31,34 |
|
|
|
|
|
|
|
|
Клітини H329:H333 =C14 – <Ctrl + Enter>
Клітини J329:J333 =МУМНОЖ(B329:F333;H329:H333) – <Ctrl + Shift + Enter>
Клітини H337:H341 =C14 – <Ctrl + Enter>
Клітини J337:J341 =МУМНОЖ(B337:F341;H337:H341) – <Ctrl + Shift + Enter>
Клітини H345:H349 =C14 – <Ctrl + Enter>
Клітини J345:J349 =МУМНОЖ(B345:F349;H345:H349) – <Ctrl + Shift + Enter>
Клітини H353:H357 =C14 – <Ctrl + Enter>
Клітини J353:J357 =МУМНОЖ(B353:F357;H353:H357) – <Ctrl + Shift + Enter>
Зсув елементів двовимірного масиву
Зсув стовпців матриці
|
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
363 |
|
На 1-н рядок вправо |
|
|
|
|
|
|
|
|
|
|
|
|
|||
364 |
A |
--> |
|
|
|
|
Z1 |
|
|
|
|
|
Az1 |
|
|
|
|
365 |
0,10 |
8,11 |
40,44 |
65,52 |
57,51 |
|
0 |
1 |
0 |
0 |
0 |
|
57,51 |
0,10 |
8,11 |
40,44 |
65,52 |
366 |
1,20 |
2,97 |
6,75 |
12,61 |
14,10 |
* |
0 |
0 |
1 |
0 |
0 |
= |
14,10 |
1,20 |
2,97 |
6,75 |
12,61 |
367 |
1,29 |
11,08 |
47,19 |
78,13 |
71,61 |
|
0 |
0 |
0 |
1 |
0 |
|
71,61 |
1,29 |
11,08 |
47,19 |
78,13 |
368 |
2,49 |
14,05 |
53,95 |
90,75 |
85,70 |
|
0 |
0 |
0 |
0 |
1 |
|
85,70 |
2,49 |
14,05 |
53,95 |
90,75 |
369 |
3,79 |
25,13 |
101,14 |
168,88 |
157,31 |
|
1 |
0 |
0 |
0 |
0 |
|
157,31 |
3,79 |
25,13 |
101,14 |
168,88 |
370 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
371 |
|
На 2-а рядки вправо |
|
|
|
|
|
|
|
|
|
|
|
|
|||
372 |
A |
--> |
|
|
|
|
Z2 |
|
|
|
|
|
Az2 |
|
|
|
|
373 |
0,10 |
8,11 |
40,44 |
65,52 |
57,51 |
|
0 |
0 |
1 |
0 |
0 |
|
65,52 |
57,51 |
0,10 |
8,11 |
40,44 |
374 |
1,20 |
2,97 |
6,75 |
12,61 |
14,10 |
* |
0 |
0 |
0 |
1 |
0 |
= |
12,61 |
14,10 |
1,20 |
2,97 |
6,75 |
375 |
1,29 |
11,08 |
47,19 |
78,13 |
71,61 |
|
0 |
0 |
0 |
0 |
1 |
|
78,13 |
71,61 |
1,29 |
11,08 |
47,19 |
376 |
2,49 |
14,05 |
53,95 |
90,75 |
85,70 |
|
1 |
0 |
0 |
0 |
0 |
|
90,75 |
85,70 |
2,49 |
14,05 |
53,95 |
377 |
3,79 |
25,13 |
101,14 |
168,88 |
157,31 |
|
0 |
1 |
0 |
0 |
0 |
|
168,88 |
157,31 |
3,79 |
25,13 |
101,14 |
378 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
379 |
|
На 1-н рядок вліво |
|
|
|
|
|
|
|
|
|
|
|
|
|||
380 |
A |
<-- |
|
|
|
|
1Z |
|
|
|
|
|
Az1 |
|
|
|
|
381 |
0,10 |
8,11 |
40,44 |
65,52 |
57,51 |
|
0 |
0 |
0 |
0 |
1 |
|
8,11 |
40,44 |
65,52 |
57,51 |
0,10 |
382 |
1,20 |
2,97 |
6,75 |
12,61 |
14,10 |
* |
1 |
0 |
0 |
0 |
0 |
= |
2,97 |
6,75 |
12,61 |
14,10 |
1,20 |
383 |
1,29 |
11,08 |
47,19 |
78,13 |
71,61 |
|
0 |
1 |
0 |
0 |
0 |
|
11,08 |
47,19 |
78,13 |
71,61 |
1,29 |
384 |
2,49 |
14,05 |
53,95 |
90,75 |
85,70 |
|
0 |
0 |
1 |
0 |
0 |
|
14,05 |
53,95 |
90,75 |
85,70 |
2,49 |
385 |
3,79 |
25,13 |
101,14 |
168,88 |
157,31 |
|
0 |
0 |
0 |
1 |
0 |
|
25,13 |
101,14 |
168,88 |
157,31 |
3,79 |
386 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
387 |
|
На 2-a рядки вліво |
|
|
|
|
|
|
|
|
|
|
|
|
|||
388 |
A |
<-- |
|
|
|
|
2Z |
|
|
|
|
|
Az2 |
|
|
|
|
389 |
0,10 |
8,11 |
40,44 |
65,52 |
57,51 |
|
0 |
0 |
0 |
1 |
0 |
|
40,44 |
65,52 |
57,51 |
0,10 |
8,11 |
390 |
1,20 |
2,97 |
6,75 |
12,61 |
14,10 |
* |
0 |
0 |
0 |
0 |
1 |
= |
6,75 |
12,61 |
14,10 |
1,20 |
2,97 |
391 |
1,29 |
11,08 |
47,19 |
78,13 |
71,61 |
|
1 |
0 |
0 |
0 |
0 |
|
47,19 |
78,13 |
71,61 |
1,29 |
11,08 |
392 |
2,49 |
14,05 |
53,95 |
90,75 |
85,70 |
|
0 |
1 |
0 |
0 |
0 |
|
53,95 |
90,75 |
85,70 |
2,49 |
14,05 |
393 |
3,79 |
25,13 |
101,14 |
168,88 |
157,31 |
|
0 |
0 |
1 |
0 |
0 |
|
101,14 |
168,88 |
157,31 |
3,79 |
25,13 |
Клітини B365:F369 =C48 – <Ctrl + Enter>
Клітини N365:R369 =МУМНОЖ(B365:F369;H365:L369) – <Ctrl + Shift + Enter>
Клітини B373:F377 =C48 – <Ctrl + Enter>
Клітини N373:R377 =МУМНОЖ(B373:F377;H373:L377) – <Ctrl + Shift + Enter>
Клітини B381:F385 =C48 – <Ctrl + Enter>
Клітини N381:R385 =МУМНОЖ(B381:F385;H381:L385) – <Ctrl + Shift + Enter>
Клітини B389:F393 =C48 – <Ctrl + Enter>
Клітини N389:R393 =МУМНОЖ(B389:F393;H389:L393) – <Ctrl + Shift + Enter>
Зсув рядків матриці
|
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
397 |
На 1-н рядок вверх |
|
|
|
|
|
|
|
|
|
|
|
|
||||
398 |
Z1 |
|
|
|
|
|
A |
|
|
|
|
|
Az1 |
|
|
|
|
399 |
0 |
1 |
0 |
0 |
0 |
|
0,10 |
8,11 |
40,44 |
65,52 |
57,51 |
|
1,20 |
2,97 |
6,75 |
12,61 |
14,10 |
400 |
0 |
0 |
1 |
0 |
0 |
* |
1,20 |
2,97 |
6,75 |
12,61 |
14,10 |
= |
1,29 |
11,08 |
47,19 |
78,13 |
71,61 |
401 |
0 |
0 |
0 |
1 |
0 |
|
1,29 |
11,08 |
47,19 |
78,13 |
71,61 |
|
2,49 |
14,05 |
53,95 |
90,75 |
85,70 |
402 |
0 |
0 |
0 |
0 |
1 |
|
2,49 |
14,05 |
53,95 |
90,75 |
85,70 |
|
3,79 |
25,13 |
101,14 |
168,88 |
157,31 |
403 |
1 |
0 |
0 |
0 |
0 |
|
3,79 |
25,13 |
101,14 |
168,88 |
157,31 |
|
0,10 |
8,11 |
40,44 |
65,52 |
57,51 |
404 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
405 |
На 2-а рядки вверх |
|
|
|
|
|
|
|
|
|
|
|
|
||||
406 |
Z2 |
|
|
|
|
|
A |
|
|
|
|
|
Az2 |
|
|
|
|
407 |
0 |
0 |
1 |
0 |
0 |
|
0,10 |
8,11 |
40,44 |
65,52 |
57,51 |
|
1,29 |
11,08 |
47,19 |
78,13 |
71,61 |
408 |
0 |
0 |
0 |
1 |
0 |
* |
1,20 |
2,97 |
6,75 |
12,61 |
14,10 |
= |
2,49 |
14,05 |
53,95 |
90,75 |
85,70 |
409 |
0 |
0 |
0 |
0 |
1 |
|
1,29 |
11,08 |
47,19 |
78,13 |
71,61 |
|
3,79 |
25,13 |
101,14 |
168,88 |
157,31 |
410 |
1 |
0 |
0 |
0 |
0 |
|
2,49 |
14,05 |
53,95 |
90,75 |
85,70 |
|
0,10 |
8,11 |
40,44 |
65,52 |
57,51 |
411 |
0 |
1 |
0 |
0 |
0 |
|
3,79 |
25,13 |
101,14 |
168,88 |
157,31 |
|
1,20 |
2,97 |
6,75 |
12,61 |
14,10 |
412 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
413 |
На 1-н рядок вниз |
|
|
|
|
|
|
|
|
|
|
|
|
||||
414 |
1Z |
|
|
|
|
|
A |
|
|
|
|
|
Az1 |
|
|
|
|
415 |
0 |
0 |
0 |
0 |
1 |
|
0,10 |
8,11 |
40,44 |
65,52 |
57,51 |
|
3,79 |
25,13 |
101,14 |
168,88 |
157,31 |
416 |
1 |
0 |
0 |
0 |
0 |
* |
1,20 |
2,97 |
6,75 |
12,61 |
14,10 |
= |
0,10 |
8,11 |
40,44 |
65,52 |
57,51 |
417 |
0 |
1 |
0 |
0 |
0 |
|
1,29 |
11,08 |
47,19 |
78,13 |
71,61 |
|
1,20 |
2,97 |
6,75 |
12,61 |
14,10 |
418 |
0 |
0 |
1 |
0 |
0 |
|
2,49 |
14,05 |
53,95 |
90,75 |
85,70 |
|
1,29 |
11,08 |
47,19 |
78,13 |
71,61 |
419 |
0 |
0 |
0 |
1 |
0 |
|
3,79 |
25,13 |
101,14 |
168,88 |
157,31 |
|
2,49 |
14,05 |
53,95 |
90,75 |
85,70 |
420 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
421 |
На 2-a рядки вниз |
|
|
|
|
|
|
|
|
|
|
|
|
||||
422 |
2Z |
|
|
|
|
|
A |
|
|
|
|
|
Az2 |
|
|
|
|
418 |
0 |
0 |
0 |
1 |
0 |
|
0,10 |
8,11 |
40,44 |
65,52 |
57,51 |
|
2,49 |
14,05 |
53,95 |
90,75 |
85,70 |
419 |
0 |
0 |
0 |
0 |
1 |
* |
1,20 |
2,97 |
6,75 |
12,61 |
14,10 |
= |
3,79 |
25,13 |
101,14 |
168,88 |
157,31 |
420 |
1 |
0 |
0 |
0 |
0 |
|
1,29 |
11,08 |
47,19 |
78,13 |
71,61 |
|
0,10 |
8,11 |
40,44 |
65,52 |
57,51 |
421 |
0 |
1 |
0 |
0 |
0 |
|
2,49 |
14,05 |
53,95 |
90,75 |
85,70 |
|
1,20 |
2,97 |
6,75 |
12,61 |
14,10 |
422 |
0 |
0 |
1 |
0 |
0 |
|
3,79 |
25,13 |
101,14 |
168,88 |
157,31 |
|
1,29 |
11,08 |
47,19 |
78,13 |
71,61 |
Клітини H399:L403 =C48 – <Ctrl + Enter>
Клітини N399:R403 =МУМНОЖ(B399:F403;H399:L403) – <Ctrl + Shift + Enter>
Клітини H407:L411 =C48 – <Ctrl + Enter>
Клітини N407:R411 =МУМНОЖ(B407:F411;H407:L411) – <Ctrl + Shift + Enter>
Клітини H415:L419 =C48 – <Ctrl + Enter>
Клітини N415:R419 =МУМНОЖ(B415:F419;H415:L419) – <Ctrl + Shift + Enter>
Клітини H423:L427 =C48 – <Ctrl + Enter>
Клітини N423:R427 =МУМНОЖ(B423:F427;H423:L427) – <Ctrl + Shift + Enter>
Задача 6.6. Задано дійсне число x=1.32№ (де № – номер варіанту). Відповідно до номера варіанту (прикл. 1 і 2) у середовищі Excel скласти програму для обчислення значень:
степеневого многочлена 3-го степеня за такою формулою
![]() ;
;
першої та другої похідної від степеневого многочлена 3-го степеня за такими формулами:
![]() ,
,
![]() ;
;
невизначеного інтегралу від степеневого многочлена 3-го степеня за такою формулою
![]() .
.
Обчислення значення степеневого многочлена
|
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
438 |
|
|
|
|
|
Aт |
|
|
|
|
|
|
|
|
439 |
X |
|
|
|
|
a0 |
|
|
|
|
|
|
|
|
440 |
1 |
x |
x2/2! |
x3/3! |
* |
a1 |
= |
y |
|
|
|
|
|
|
441 |
|
|
|
|
|
a2 |
|
|
|
|
|
|
|
|
442 |
|
|
|
|
|
a3 |
|
|
|
|
|
|
|
|
443 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
444 |
|
х= |
2,5 |
|
|
|
|
|
|
|
|
|
|
|
445 |
X |
|
|
|
|
Aт |
|
|
|
|
|
|
|
|
446 |
0 |
1 |
2 |
3 |
|
2,24 |
|
y |
|
|
|
|
|
|
447 |
1 |
2,5 |
3,125 |
2,604 |
* |
13,5 |
= |
35,411 |
|
|
|
|
|
|
448 |
|
|
|
|
|
0,034 |
|
|
|
|
|
|
|
|
449 |
|
|
|
|
|
-0,263 |
|
|
|
|
|
|
|
|
Клітини B447:E447 =$D$444^B$446/ФАКТР(B$446) – <Ctrl + Enter>
Клітини G446:G449 довільні числа в межах від -5 до +20
Клітини I447 =МУМНОЖ(B447:E447;G446:G449) – <Ctrl + Shift + Enter>
Обчислення значення похідної від степеневого многочлена
452 |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
453 |
|
|
|
|
|
D1 |
|
|
|
|
Aт |
|
|
|
454 |
X |
|
|
|
|
0 |
1 |
0 |
0 |
|
a0 |
|
|
|
455 |
1 |
x |
x2/2! |
x3/3! |
* |
0 |
0 |
1 |
0 |
* |
a1 |
= |
dy/dx |
|
456 |
|
|
|
|
|
0 |
0 |
0 |
1 |
|
a2 |
|
|
|
457 |
|
|
|
|
|
0 |
0 |
0 |
0 |
|
a3 |
|
|
|
458 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
459 |
1-а похідна |
|
|
|
|
|
|
|
|
|
|
|
|
|
460 |
|
|
|
|
|
D1 |
|
|
|
|
|
|
|
|
461 |
X |
|
|
|
|
0 |
1 |
0 |
0 |
|
X*D1 |
|
|
|
462 |
1 |
2,5 |
3,125 |
2,604 |
* |
0 |
0 |
1 |
0 |
= |
0 |
1 |
2,50 |
3,125 |
463 |
|
|
|
|
|
0 |
0 |
0 |
1 |
|
|
|
|
|
464 |
|
|
|
|
|
0 |
0 |
0 |
0 |
|
|
|
|
|
465 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
466 |
|
|
|
|
|
Aт |
|
|
|
|
|
|
|
|
467 |
X*D1 |
|
|
|
|
2,24 |
|
dy/dx |
|
|
|
|
|
|
468 |
0 |
1 |
2,50 |
3,125 |
* |
13,5 |
= |
12,763 |
|
|
|
|
|
|
469 |
|
|
|
|
|
0,034 |
|
|
|
|
|
|
|
|
470 |
|
|
|
|
|
-0,263 |
|
|
|
|
|
|
|
|
471 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
472 |
2-а похідна |
|
|
|
|
|
|
|
|
|
|
|
|
|
473 |
|
|
|
|
|
D2 |
|
|
|
|
|
|
|
|
474 |
X |
|
|
|
|
0 |
0 |
1 |
0 |
|
X*D2 |
|
|
|
475 |
1 |
2,5 |
3,125 |
2,604 |
* |
0 |
0 |
0 |
1 |
= |
0 |
0 |
1 |
2,5 |
476 |
|
|
|
|
|
0 |
0 |
0 |
0 |
|
|
|
|
|
477 |
|
|
|
|
|
0 |
0 |
0 |
0 |
|
|
|
|
|
478 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
479 |
|
|
|
|
|
Aт |
|
|
|
|
|
|
|
|
480 |
X*D2 |
|
|
|
|
2,24 |
|
d2y/dx2 |
|
|
|
|
|
|
481 |
0 |
0 |
1 |
2,5 |
* |
13,5 |
= |
-0,624 |
|
|
|
|
|
|
482 |
|
|
|
|
|
0,034 |
|
|
|
|
|
|
|
|
483 |
|
|
|
|
|
-0,263 |
|
|
|
|
|
|
|
|
1-а похідна
Клітини B462:E462 =B447 – <Ctrl + Enter>
Клітини L462:O462 =МУМНОЖ(B462:E462;G461:J464) – <Ctrl + Shift + Enter>
Клітини B468:E468 =B462 – <Ctrl + Enter>
Клітини G467:G470 =G446 – <Ctrl + Enter>
Клітини I468 =МУМНОЖ(B468:E468;G467:G470) – <Ctrl + Shift + Enter>
2-а похідна
Клітини B475:E475 =B447 – <Ctrl + Enter>
Клітини L475:O475 =МУМНОЖ(B475:E475;G474:J477) – <Ctrl + Shift + Enter>
Клітини B481:E481 =L475 – <Ctrl + Enter>
Клітини G480:G483 =B462 – <Ctrl + Enter>
Клітини I468 =МУМНОЖ(B481:E481;G480:G483) – <Ctrl + Shift + Enter>
Обчислення значення невизначеного інтегралу від степеневого многочлена
488 |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
491 |
|
|
|
|
|
|
І |
|
|
|
|
Aт |
|
|
|
492 |
X |
|
|
|
|
|
0 |
0 |
0 |
0 |
|
a0 |
|
|
|
493 |
1 |
x |
x2/2! |
x3/3! |
x4/4! |
* |
1 |
0 |
0 |
0 |
* |
a1 |
= |
fydx |
|
494 |
|
|
|
|
|
|
0 |
1 |
0 |
0 |
|
a2 |
|
|
|
495 |
|
|
|
|
|
|
0 |
0 |
1 |
0 |
|
a3 |
|
|
|
496 |
|
|
|
|
|
|
0 |
0 |
0 |
1 |
|
|
|
|
|
497 |
|
х= |
2,5 |
|
|
|
|
|
|
|
|
|
|
|
|
498 |
X |
|
|
|
|
|
І |
|
|
|
|
|
|
|
|
499 |
0 |
1 |
2 |
3 |
4 |
|
0 |
0 |
0 |
0 |
|
X*І |
|
|
|
500 |
1 |
2,5 |
3,125 |
2,604 |
1,6276 |
* |
1 |
0 |
0 |
0 |
= |
2,5 |
3,125 |
2,604 |
1,6276 |
501 |
|
|
|
|
|
|
0 |
1 |
0 |
0 |
|
|
|
|
|
502 |
|
|
|
|
|
|
0 |
0 |
1 |
0 |
|
|
|
|
|
503 |
|
|
|
|
|
|
0 |
0 |
0 |
1 |
|
|
|
|
|
504 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
505 |
|
|
|
|
|
Aт |
|
|
|
|
|
|
|
|
|
506 |
X*І |
|
|
|
|
2,24 |
|
fydx |
|
|
|
|
|
|
|
507 |
2,5 |
3,125 |
2,604 |
1,6276 |
* |
13,5 |
= |
47,448 |
|
|
|
|
|
|
|
508 |
|
|
|
|
|
0,034 |
|
|
|
|
|
|
|
|
|
509 |
|
|
|
|
|
-0,263 |
|
|
|
|
|
|
|
|
|
Клітини B500:F500 =$D$497^B$499/ФАКТР(B$499) – <Ctrl + Enter>
Клітини M500:P500 =МУМНОЖ(B500:F500;H499:K503) – <Ctrl + Shift + Enter>
Клітини B507:E507 =M500 – <Ctrl + Enter>
Клітини G506:G509 =B462 – <Ctrl + Enter>
Клітина I507 =МУМНОЖ(B507:E507;G506:G509) – <Ctrl + Shift + Enter>
6.4. Індивідуальні завдання
Приклад 1. Задано дійсне число x=1.63№ (де № – номер варіанту) і ціле число n=10. Елементи одновимірного масиву (рядка чи стовпця) необхідно обчислити за такою формулою:
d1=0.21№; , де
1)
|
9)
|
2)
|
10)
|
3)
|
11)
|
4)
|
12)
|
5)
|
13)
|
6)
|
14)
|
7)
|
15)
|
8)
|
16)
|
Приклад 2. Задано дійсне число x=2.48№ (де № – номер варіанту) і цілі числа m=10 і n=5. Елементи двовимірного масиву (матриці)
визначаються за таким принципом:
перший рядок матриці задається такою формулою
, де
1)
|
6)
|
11)
|
2)
|
7)
|
12)
|
3)
|
8)
|
13)
|
4)
|
9)
|
14)
|
5)
|
10)
|
15)
|
другий рядок матриці задається такою формулою
![]() ,
де
,
де
1)
|
6)
|
11)
|
2)
|
7)
|
12)
|
3)
|
8)
|
13)
|
4)
|
9)
|
14)
|
5)
|
10)
|
15)
|
кожний наступний рядок є сумою двох попередніх рядків, тобто
.
Задача 6.1. Відповідно до номера варіанту (прикл. 1 і 2), з використанням засобів середовищ Excel та Visual Basic відсортувати елементи одновимірного масиву, а саме:
рядка у порядку спадання значень його елементів;
стовпця у порядку зростання значень його елементів.
Задача 6.2. Відповідно до номера варіанту (прикл. 1 і 2), з використанням засобів середовищ Excel та Visual Basic відсортувати елементи двовимірного масиву, а саме:
рядків матриці у порядку спадання значень їх елементів;
стовпців матриці у порядку зростання значень їх елементів;
матриці по рядках у порядку спадання значень їх елементів;
матриці по стовпцях у порядку зростання значень їх елементів.
Задача 6.3. Відповідно до номера варіанту (прикл. 1 і 2) у середовищі Excel скласти програму для інвертування елементів вектора-рядка/стовпця і матриці, а саме:
інвертування елементів рядка ;
інвертування елементів стовпця ;
інвертування елементів матриці по стовпцях;
інвертування елементів матриці по рядках;
інвертування елементів матриці по стовпцях і по рядках;
інвертування елементів матриці по рядках і по стовпцях.
Задача 6.4. Відповідно до номера варіанту (прикл. 1 і 2) у середовищі Excel скласти програму для перестановки елементів вектора-рядка/стовпця і матриці, а саме:
перестановка елементів рядка – останнього з передостаннім;
перестановка елементів рядка – другого з останнім;
перестановка елементів стовпця – останнього з передостаннім;
перестановка елементів стовпця – другого з останнім;
перестановка стовпців матриці – останнього з передостаннім;
перестановка стовпців матриці – другого з останнім;
перестановка рядків матриці – останнього з передостаннім;
перестановка рядків матриці – другого з останнім.
Задача 6.5. Відповідно до номера варіанту (прикл. 1 і 2) у середовищі Excel скласти програму для виконання зсуву елементів вектора-рядка/стовпця і матриці, а саме:
зсув елементів рядка – на одну позицію вправо;
зсув елементів рядка – на дві позиції вправо;
зсув елементів рядка – на одну позицію вліво;
зсув елементів рядка – на дві позиції вліво;
зсув елементів стовпця – на одну позицію вверх;
зсув елементів стовпця – на дві позиції вверх;
зсув елементів стовпця – на одну позицію вниз;
зсув елементів стовпця – на дві позиції вниз;
зсув стовпців матриці – на один стовпець вправо;
зсув стовпців матриці – на два стовпці вправо;
зсув стовпців матриці – на один стовпець вліво;
зсув стовпців матриці – на два стовпці вліво;
зсув рядків матриці – на один рядок вверх;
зсув рядків матриці – на два рядки вверх;
зсув рядків матриці – на один рядок вниз;
зсув рядків матриці – на два рядки вниз.
Задача 6.6. Задано дійсне число x=1.32№ (де № – номер варіанту). Відповідно до номера варіанту (прикл. 1 і 2) у середовищі Excel скласти програму для обчислення значень:
степеневого многочлена 3-го степеня за такою формулою
;
першої та другої похідної від степеневого многочлена 3-го степеня за такими формулами:
,
;
невизначеного інтегралу від степеневого многочлена 3-го степеня за такою формулою
.
6.5. Контрольні запитання
1. Навести приклади використання функції сторінки ИСТИНА
2. Навести приклади використання функції сторінки ЛОЖЬ
3. Навести приклади використання функції сторінки ЕСЛИ
4. Навести приклади використання функції сторінки И
5. Навести приклади використання функції сторінки ИЛИ
6. Навести приклади використання функції сторінки НЕ
7. Навести приклади використання функції перегляду і посилань ВЫБОР
8. Навести приклади використання функції функція ДЕЛЬТА
9. Навести приклади використання функції функція ПОРОГ
10. Навести приклади використання функції функція СОВПАД
Лабораторна робота №7. ВИКОРИСТАННЯ ФУНКЦІЙ КОРИСТУВАЧА
7.1. Програма роботи
7.1.1. Підготувати бланк завдання та отримати завдання.
7.1.2. Запрограмувати математичні функції згідно з вказівками до виконання роботи.
7.1.3. Підготувати власті коректні вхідні дані для кожної з виконаних задач, провести розрахунки і проаналізувати їх.
7.1.4. Оформити звіт про роботу та захистити її
7.2. Вказівки до виконання роботи
7.2.1. Зразок бланка завдання наведено на рис. 7.1. Студент, відповідно до індивідуального номера, вибирає завдання з розд. 7.5, яке складається з декількох задач, і записує їх до бланку.
7.2.2. Математичні функції необхідно запрограмувати трьома способами: з введення і без введення допоміжних змінних, а також з використанням функції користувача. Перед початком програмування математичних виразі їх потрібно проаналізувати з приводу коректного виконання для заданих вхідних даних. У випадку виявлення некоректних записів, наприклад від'ємне значення аргументу від натурального логарифма, чи дійсного степеня від від'ємного числа та ін.
7.2.3. Власних вхідних даних необхідно підготувати не менше, ніж два комплекти. Вони мають бути коректними, в розумних межах і не суперечити математичним виразам. Після проведення розрахунків необхідно їх проаналізувати і занести до звіту.
7.2.4. Звіт має містити такі розділи:
бланк завдання з записаною на ньому умовою задачі;
текст програми у режимі формул – для середовища Excel;
результати відповідних розрахунків, виконані у середовищі Excel, які передбачаються умовами задач;
аналіз отриманих результатів, висновки і пропозиції.
7.3. Зразок виконання завдання
Задача 7.1. Задано дійсні числа s=1.38№ (де № – номер варіанту) і t=5.67. Відповідно до номера варіанту потрібно розробити програму, яка б давала змогу отримати значення функції
![]() ,
,
де f[x,y,z] визначається за допомогою такого математичного виразу
![]() .
.
Тексти функцій і процедур – для середовища Visual Basic
Function FnF(x, y, z) As Single Dim f1, f2, f3 As Single f1 =Abs(x + y) ^ (1 / 3) f2 =(x ^ 2 + y) * Abs(x ^ 2 + z) ^ 0.3 f3 =Exp(z + 2.4) + y ^ 2 - 1.26 FnF =f1 * f2 / f3 End Function |
Function FnC(s, t) As Single Dim c1, c2, c3 As Single c1 =FnF(t, -2 * Abs(s) ^ 0.2, 1.17) ^ 2 + t * s c2 =FnF(2.2 * t, Abs(t - s) ^ 1.5, s - 1.7) ^ 0.6 - t c3 =FnF(2.5 * s, t ^ 3, s - t ^ 2) FnC =c1 / c2 + c3 End Function |
A |
B |
C |
D |
E |
15 |
s= |
3,5 |
t= |
5,67 |
16 |
|
|
|
|
17 |
c1= |
=FnF(E15;-2*ABS(C15)^0,2;1,17)^2 |
|
|
18 |
c2= |
=FnF(2,2*E15;ABS(E15-C15)^1,5;C15-1,7)^0,6 |
|
|
19 |
c3= |
=FnF(2,5*C15;E15^3;C15-E15^2) |
|
|
20 |
|
|
|
|
21 |
c= |
(C17+E15*C15)/(C18-E15)+C19 |
|
|
22 |
c'= |
=FnC(C15;E15) |
|
|
Результати розрахунку, виконані у середовищі Excel
-
A
B
C
D
E
15
s=
3,5
t=
5,67
16
17
c1=
9,1337
18
c2=
6,7254
19
c3=
0,1432
20
21
c=
27,6011
22
c'=
27,6011
Задано sп=-10, sк=10, s=2, y=4.7, z=1.32. Відповідно до номера варіанту потрібно розробити програму для одновимірного табулювання функцій c1[x,y,z], c2[x,y,z], c3[x,y,z], ce[s,t] і cf[s,t] за незалежною змінною Х згідно з математичними виразами, наведеними вище. Побудувати одновимірні графіки цих функцій.
Текст програми у режимі формул – для середовища Excel
Клітина B33 =C28 – <Enter>
Клітини B34:B43 =B33+$G$28 – <Ctrl + Enter>
Клітина C33:C43 =FnF($C$29;-2*ABS(B33)^0,2;1,17)^2 – <Ctrl + Enter>
Клітина D33:D43 =FnF(2,2*$C$29;ABS($C$29-B33)^1,5;B33-1,7)^0,6 – <Ctrl + Enter>
Клітина E33:E43 =FnF(2,5*B33;$C$29^3;B33-$C$29^2) – <Ctrl + Enter>
Клітина F33:F43 =(C33+$C$29*B33)/(D33-$C$29)+E33 – <Ctrl + Enter>
Клітина G33:G43 =FnC(B33;$C$29) – <Ctrl + Enter>
Результати розрахунку, виконані у середовищі Excel
A |
B |
C |
D |
E |
F |
G |
28 |
sп= |
-10 |
sк= |
10 |
s= |
2 |
29 |
t= |
5,67 |
|
|
|
|
30 |
|
|
|
|
|
|
31 |
s |
c1[x,y,z] |
c2[x,y,z] |
c3[x,y,z] |
ce[s,t] |
cf[s,t] |
32 |
|
|
|
|
|
|
33 |
-10,0 |
6,460 |
1,034 |
0,8860 |
11,7228 |
11,7228 |
34 |
-8,0 |
7,030 |
1,241 |
0,5588 |
9,2126 |
9,2126 |
35 |
-6,0 |
7,766 |
1,543 |
0,3244 |
6,6865 |
6,6865 |
36 |
-4,0 |
8,798 |
2,020 |
0,1645 |
3,9674 |
3,9674 |
37 |
-2,0 |
10,509 |
2,849 |
0,0681 |
0,3626 |
0,3626 |
38 |
0,0 |
22,953 |
4,529 |
0,0881 |
-20,0247 |
-20,0247 |
39 |
2,0 |
10,509 |
7,937 |
0,0584 |
9,6968 |
9,6968 |
40 |
4,0 |
8,798 |
5,187 |
0,1768 |
-65,0103 |
-65,0103 |
41 |
6,0 |
7,766 |
1,539 |
0,3491 |
-9,7663 |
-9,7663 |
42 |
8,0 |
7,030 |
0,492 |
0,6093 |
-9,5091 |
-9,5091 |
43 |
10,0 |
6,460 |
0,161 |
0,9813 |
-10,4831 |
-10,4831 |

Задача 7.2. Задано дійсне число y=1.65№ (де № – номер варіанту) і додатне ціле m=5. Відповідно до номера варіанту потрібно розробити програму, яка б дала змогу отримати
![]() ,
,
де t[x,n] визначається з такого співвідношення:

Тексти функцій і процедур – для середовища Visual Basic
Function FnZ(y, m) As Single
Dim z1, z2, z3, z4, z5 As Single
z1 =FnT(y + 0.1, m ^ 0.2 - 1) ^ 2
z2 =FnT(m + y ^ 2, y + 3)
z3 =FnT(y ^ 2 + 1.1, y * m ^ 0.3) ^ (2 / 3)
z4 =1.23 + z1 - Abs(y * z2) ^ (2 / m)
z5 =2.6 + z3 + Abs(y / m) ^ (1 / 3)
FnZ =z4 / z5
End Function
Function FnT(i, j) As Single
Dim c As Single
c =j * Log(Abs(i + j) ^ 0.56) ^ 2
c =Abs(i) ^ 0.13 - c / (i * 3.6 + 0.25)
If (i >= j) And (i < 2 * j) Then
c =3 * Cos(i ^ 2 - j / 6) ^ 2
c =c / Log(Abs(i + j - 0.11) ^ 1.3) ^ 2
End If
If i < j Then c =1 + i * j ^ 2 + Sin(i ^ 3) ^ 2
FnT =c
End Function
або
Function FnT1(i, j) As Single
Dim c As Single
If (i >= j) And (i < 2 * j) Then
c =3 * Cos(i ^ 2 - j / 6) ^ 2
FnT1 =c / Log(Abs(i + j - 0.11) ^ 1.3) ^ 2
ElseIf i < j Then FnT1 =1 + i * j ^ 2 + Sin(i ^ 3) ^ 2
Else
c =j * Log(Abs(i + j) ^ 0.56) ^ 2
FnT1 =Abs(i) ^ 0.13 - c / (i * 3.6 + 0.25)
End If
End Function
A |
B |
C |
D |
E |
65 |
y= |
4,65 |
m= |
5 |
66 |
|
|
|
|
67 |
z1= |
=FnT(C65+0,1;E65^0,2-1)^2 |
|
|
68 |
z2= |
=FnT(E65+C65^2;C65+3) |
|
|
69 |
z3= |
=FnT(C65^2+1,1;C65*E65^0,3)^(2/3) |
|
|
70 |
z4= |
=1,23+C67-Abs(C65*C68)^(2/E65) |
|
|
71 |
z5= |
=2,6+C69+Abs(C65/E65)^(1/3) |
|
|
72 |
|
|
|
|
73 |
z= |
=C70/C71 |
|
|
74 |
z'= |
=FnZ(C65;E65) |
|
|
Результати розрахунку, виконані у середовищі Excel
-
A
B
C
D
E
65
y=
4,65
m=
5
66
67
z1=
1,4549
68
z2=
1,2202
69
z3=
1,1078
70
z4=
0,6825
71
z5=
4,6839
72
73
z=
0,1457
74
z'=
0,1457
Задано yп=-5, yк=5, y=1, m=5. Відповідно до номера варіанту потрібно розробити програму для одновимірного табулювання функцій t1[i,j], t2[i,j], t3[i,j], ze[y,m] і zf[y,m] за незалежною змінною Х згідно з математичними виразами, наведеними вище. Побудувати одновимірні графіки цих функцій.
Текст програми у режимі формул – для середовища Excel
Клітина B84 =C79 – <Enter>
Клітини B85:B94 =B84+$G$79 – <Ctrl + Enter>
Клітини C84:C94 =1,23+FnT(B84+0,1;$C$80^0,2-1)^2 – <Ctrl + Enter>
Клітини D81:D94 =Abs(B84*FnT($C$80+B84^2;B84+3))^(2/$C$80) – <Ctrl + Enter>
Клітини E81:E94 =2,6+FnT(B84^2+1,1;B84*$C$80^0,3)^(2/3)+ABS(B84/$C$80)^(1/3) – <Ctrl + Enter>
Клітини F81:F94 (C84-D84)/E84 – <Ctrl + Enter>
Клітини G81:G94 =FnZ(B84;$C$80) – <Ctrl + Enter>
Результати розрахунку, виконані у середовищі Excel
A |
B |
C |
D |
E |
F |
G |
79 |
yп= |
-5 |
yк= |
5 |
y= |
1 |
80 |
m= |
5 |
|
|
|
|
81 |
|
|
|
|
|
|
82 |
y |
t1[i,j] |
t2[i,j] |
t3[i,j] |
ze[y,m] |
zf[y,m] |
83 |
|
|
|
|
|
|
84 |
-5,0 |
2,837 |
2,309 |
5,0541 |
0,1045 |
0,1045 |
85 |
-4,0 |
1,554 |
2,060 |
4,9133 |
-0,1030 |
-0,1030 |
86 |
-3,0 |
2,312 |
1,780 |
4,7333 |
0,1124 |
0,1124 |
87 |
-2,0 |
2,276 |
1,456 |
4,5015 |
0,1820 |
0,1820 |
88 |
-1,0 |
2,956 |
1,053 |
4,2738 |
0,4453 |
0,4453 |
89 |
0,0 |
2,259 |
0,000 |
3,6083 |
0,6261 |
0,6261 |
90 |
1,0 |
2,246 |
0,495 |
3,6488 |
0,4800 |
0,4800 |
91 |
2,0 |
2,415 |
0,076 |
3,8389 |
0,6093 |
0,6093 |
92 |
3,0 |
2,535 |
1,598 |
4,4738 |
0,2094 |
0,2094 |
93 |
4,0 |
2,631 |
1,850 |
4,6054 |
0,1694 |
0,1694 |
94 |
5,0 |
2,712 |
2,081 |
4,7240 |
0,1336 |
0,1336 |

Задача 7.3. Задано дійсне число s=1.75№ (де № – номер варіанту) і додатне ціле t=5. Відповідно до номера варіанту потрібно розробити програму, яка б давала змогу отримати значення функції
![]() ,
,
де g[x,n] і q[x,n] визначаються за допомогою таких математичних виразів:
![]() і
і ![]() .
.
Тексти функцій і процедур – для середовища Visual Basic
Function FnG(x, n) As Single
Dim g As Single
Dim i As Byte
g =0
For i =1 To n
g =g + (x + Faktr(i)) / (i ^ 2 - x + 1.3)
Next i
FnG =g + x * n / n ^ x
End Function
Function FnQ(x, n) As Single
Dim q As Single
Dim i As Byte
q =1
For i =1 To n
q =q * ((x + i) / (i ^ 2 + 2 * Faktr(i) + 3) - x ^ (1 / i))
Next i
FnQ =q
End Function
Function FnP(s, t) As Single
Dim g1, g2, q1, q2 As Single
g1 =Abs(FnG(1.2 * s ^ 2, t) + s / t) ^ (1 / 3)
g2 =FnG(t ^ 2 + s, t + 2) ^ 0.8
q1 =FnQ(s ^ 2 + 3.1, 2 * t)
q2 =Sqr(Abs(FnQ(2 * s ^ 2 + t, t - 2) - t / (s + 0.1)))
FnP =g1 * g2 / q1 - q2
End Function
A |
B |
C |
D |
E |
109 |
s= |
3,76 |
t= |
5 |
110 |
|
|
|
|
111 |
g1= |
=ABS(FnG(1,2*C109^2;E109)+C109/E109)^(1/3) |
|
|
112 |
g2= |
=FnG(E109^2+C109;E109+2)^0,8 |
|
|
113 |
q1= |
=FnQ(C109^2+3,1;2*E109) |
|
|
114 |
q2= |
=КОРЕНЬ(ABS(FnQ(2*C109^2+E109;E109-2)-E109/(C109+0,1))) |
|
|
115 |
|
|
|
|
116 |
p= |
=C111*C112/C113-C114 |
|
|
117 |
p'= |
=FnP(C109;E109) |
|
|
Результати розрахунку, виконані у середовищі Excel
A |
B |
C |
D |
E |
109 |
s= |
3,76 |
t= |
5 |
110 |
|
|
|
|
111 |
g1= |
5,0846 |
|
|
112 |
g2= |
83,8148 |
|
|
113 |
q1= |
1068,6981 |
|
|
114 |
q2= |
11,0306 |
|
|
115 |
|
|
|
|
116 |
p= |
-10,6318 |
|
|
117 |
p'= |
-10,6318 |
|
|
Задано sп=-5, sк=5, s=1, t=5. Відповідно до номера варіанту потрібно розробити програму для одновимірного табулювання функцій g1[x,n], g2[x,n]/q1[x,n], q2[x,n], pe[s,t] і pf[s,t] за незалежною змінною Х згідно з математичними виразами, наведеними вище. Побудувати одновимірні графіки цих функцій.
Текст програми у режимі формул – для середовища Excel
Клітина B127 =C122 – <Enter>
Клітини B128:B137 =B127+$G$122 – <Ctrl + Enter>
Клітини C127:C137 =ABS(FnG(1,2*B127^2;$C$123)+B127/$C$123)^(1/3) – <Ctrl + Enter>
Клітини D127:D137=FnG($C$123^2+B127;$C$123+2)^0,2/FnQ(B127^2+3,1;2*$C$123) – <Ctrl + Enter>
Клітини E127:E137 =КОРЕНЬ(ABS(FnQ(2*B127^2+$C$123;$C$123-2)-$C$123/ (B127+0,1))) – <Ctrl + Enter>
Клітини F127:F137 =C127*D127-E127 – <Ctrl + Enter>
Клітини G127:G137 =FnP(B127;$C$123) – <Ctrl + Enter>
Результати розрахунку, виконані у середовищі Excel
A |
B |
C |
D |
E |
F |
G |
122 |
sп= |
-5 |
sк= |
5 |
s= |
1 |
123 |
t= |
5 |
|
|
|
|
124 |
|
|
|
|
|
|
125 |
s |
g1[x,n] |
g2[x,n]/q1[x,n] |
q2[x,n] |
pe[s,t] |
pf[s,t] |
126 |
|
|
|
|
|
|
127 |
-5,0 |
3,685 |
0,001 |
11,8504 |
-11,8467 |
-11,7598 |
128 |
-4,0 |
2,117 |
0,002 |
11,3277 |
-11,3230 |
-11,2066 |
129 |
-3,0 |
2,889 |
0,007 |
9,0925 |
-9,0737 |
-8,5821 |
130 |
-2,0 |
2,757 |
0,026 |
6,1364 |
-6,0646 |
-4,0813 |
131 |
-1,0 |
2,199 |
0,121 |
3,1528 |
-2,8874 |
4,9655 |
132 |
0,0 |
1,944 |
0,279 |
7,6687 |
-7,1261 |
10,9192 |
133 |
1,0 |
2,226 |
0,145 |
4,4767 |
-4,1538 |
12,6825 |
134 |
2,0 |
2,792 |
0,020 |
6,5321 |
-6,4764 |
-5,8180 |
135 |
3,0 |
2,841 |
0,006 |
9,2742 |
-9,2563 |
-8,8291 |
136 |
4,0 |
1,990 |
0,002 |
11,4376 |
-11,4330 |
-11,3092 |
137 |
5,0 |
3,635 |
0,001 |
11,9345 |
-11,9306 |
-11,8147 |

Задача 7.4. Задано дійсне число s=1.32№ (де № – номер варіанту) і додатне ціле t=3. Відповідно до номера варіанту потрібно розробити програму, яка б давала змогу отримати значення функції
 ,
,
де h[x,y] визначається за допомогою такого математичного виразу:
![]() .
.
Тексти функцій і процедур – для середовища Visual Basic
Function Max(a, b) As Single
If a > b Then Max =a else Max =b
End Function
Function Min(a, b) As Single
If a < b Then Min =a else Min =b
End Function
Function FnH(x, y) As Single
Dim h, z, c As Single
Dim i As Byte
h =0: z =-1: i =1
c =(i + Cos(y + i)) / (1.23 + x ^ 2 + Faktr(i))
Do While Abs(c) >= 0.001
h =h + z * c
z =-z: i =i + 1
c =(i * x + Cos(y + i)) / (1.23 + x ^ 2 + Faktr(i))
Loop
FnH =h
End Function
Function FnW(s, t) As Single
Dim h1, h2, h3, h4, h5 As Single
h1 =Abs(FnH(s, t) + s / (t + 0.1)) ^ (1 / 3)
h2 =FnH(s - t, s * t) ^ 2
h3 =FnH(s * t, s + t) ^ 2
h4 =Abs(FnH(1 - s, t ^ 2)) ^ (1 / 2)
h5 =(FnH(t - s * t, s ^ 2) ^ 2) ^ (1 / 3)
FnW =h1 + Max(h2, h3) / Min(h4, h5)
End Function
A |
B |
C |
D |
E |
153 |
s= |
7,45 |
t= |
3 |
154 |
|
|
|
|
155 |
h1= |
=ABS(FnH(C153;E153)+C153/(E153+0,1))^(1/3) |
|
|
156 |
h2= |
=FnH(C153-E153;C153*E153)^2 |
|
|
157 |
h3= |
=FnH(C153*E153;C153+E153)^2 |
max(h2; h3)= |
=МАКС(C156:C157) |
158 |
h4= |
=ABS(FnH(1-C153;E153^2))^(1/2) |
|
|
159 |
h5= |
=(FnH(E153-C153*E153;C153^2)^2)^(1/3) |
min(h4; h5)= |
=МИН(C158:C159) |
160 |
|
|
|
|
161 |
w= |
=C155+E157/E159 |
|
|
162 |
w'= |
=FnW(C153;E153) |
|
|
Результати розрахунку, виконані у середовищі Excel
A |
B |
C |
D |
E |
153 |
s= |
7,45 |
t= |
3 |
154 |
|
|
|
|
155 |
h1= |
1,3573 |
|
|
156 |
h2= |
0,0168 |
|
|
157 |
h3= |
0,0010 |
max(h2; h3)= |
0,0168 |
158 |
h4= |
0,3627 |
|
|
159 |
h5= |
0,1118 |
min(h4; h5)= |
0,1118 |
160 |
|
|
|
|
161 |
w= |
1,5072 |
|
|
162 |
w'= |
1,5072 |
|
|
Задано sп=-5, sк=5, s=1, t=3. Відповідно до номера варіанту потрібно розробити програму для одновимірного табулювання функцій h1[x,y], max(h2; h3), min(h4; h5), we[s,t] і wf[s,t] за незалежною змінною Х згідно з математичними виразами, наведеними вище. Побудувати одновимірні графіки цих функцій.
Текст програми у режимі формул – для середовища Excel
Клітина B172 =C167 – <Enter>
Клітини B173:B182 =B172+$G$167 – <Ctrl + Enter>
Клітини C172:C182 =ABS(FnH(B172;$C$168)+B172/($C$168+0,1))^(1/3) – <Ctrl + Enter>
Клітини D172:D182 =max(FnH(B172-$C$168;B172*$C$168)^2;FnH(B172*$C$168;B172+ $C$168)^2) – <Ctrl + Enter>
Клітини E172:E182 =min(ABS(FnH(1-B172;$C$168^2))^(1/2);(FnH($C$168-B172*$C$168; B172^2)^2)^(1/3)) – <Ctrl + Enter>
Клітини F172:F182 =C172+D172/E172 – <Ctrl + Enter>
Клітини G172:G182 =FnW(B172;$C$168) – <Ctrl + Enter>
Результати розрахунку, виконані у середовищі Excel
A |
B |
C |
D |
E |
F |
G |
167 |
sп= |
-5 |
sк= |
5 |
s= |
1 |
168 |
t= |
3 |
|
|
|
|
169 |
|
|
|
|
|
|
170 |
s |
h1[x,y] |
max(h2; h3) |
min(h4; h5) |
we[s,t] |
wf[s,t] |
171 |
|
|
|
|
|
|
172 |
-5,0 |
1,212 |
0,012 |
0,0957 |
1,3327 |
1,3327 |
173 |
-4,0 |
1,141 |
0,019 |
0,1104 |
1,3116 |
1,3116 |
174 |
-3,0 |
1,064 |
0,022 |
0,1344 |
1,2289 |
1,2289 |
175 |
-2,0 |
0,982 |
0,040 |
0,1705 |
1,2184 |
1,2184 |
176 |
-1,0 |
0,878 |
0,040 |
0,2229 |
1,0592 |
1,0592 |
177 |
0,0 |
0,554 |
0,104 |
0,1561 |
1,2199 |
1,2199 |
178 |
1,0 |
0,750 |
0,092 |
0,3921 |
0,9832 |
0,9832 |
179 |
2,0 |
0,927 |
0,525 |
0,4204 |
2,1753 |
2,1753 |
180 |
3,0 |
1,037 |
0,024 |
0,2717 |
1,1239 |
1,1239 |
181 |
4,0 |
1,127 |
0,074 |
0,1971 |
1,5042 |
1,5042 |
182 |
5,0 |
1,204 |
0,023 |
0,1579 |
1,3520 |
1,3520 |

7.4. Індивідуальні завдання
Задача 7.1. Задано дійсні числа s=1.72№ (де № – номер варіанту) і ціле число t=2. Відповідно до номера варіанту потрібно розробити програму, яка б давала змогу отримати значення функції
![]()
де f[x,y,z] визначається з таких математичних виразів:
1)
|
2)
|
3)
|
4)
|
5)
|
6)
|
7)
|
8)
|
9)
|
10)
|
11)
|
12)
|
13)
|
14)
|
15)
|
16)
|
Задано sп=-10, sк=10, s=2, y=4.7, z=1.32. Відповідно до номера варіанту потрібно розробити програму для одновимірного табулювання функцій c1[x,y,z], c2[x,y,z], c3[x,y,z], ce[s,t] і cf[s,t] за незалежною змінною Х згідно з математичними виразами, наведеними вище. Побудувати одновимірні графіки цих функцій.
Задача 7.2. Задано дійсне число y=0.82№ (де № – номер варіанту) і додатне ціле m=5. Відповідно до номера варіанту потрібно розробити програму, яка б давала змогу отримати значення функції
![]() ,
,
де t[i,j] визначається за допомогою таких логічних виразів:
1) |
2)
|
3)
|
4)
|
5)
|
6)
|
7)
|
8)
|
9)
|
10) |
11)
|
12) |
13)
|
14)
|
15) |
16)
|
Задано sп=-5, sк=5, s=1, t=5. Відповідно до номера варіанту потрібно розробити програму для одновимірного табулювання функцій g1[x,n], g2[x,n]/q1[x,n], q2[x,n], pe[s,t] і pf[s,t] за незалежною змінною Х згідно з математичними виразами, наведеними вище. Побудувати одновимірні графіки цих функцій.
Задача 7.3. Задано дійсне число y=1.88№ (де № – номер варіанту) і додатне ціле t=5. Відповідно до номера варіанту потрібно розробити програму, яка б давала змогу отримати значення функції
![]() ,
,
де функція g[x,n] визначається з таких математичних виразів:
1)
|
6)
|
11)
|
2)
|
7)
|
12)
|
3)
|
8)
|
13)
|
4)
|
9)
|
14)
|
5)
|
10)
|
15)
|
Функція q[x,n] визначається за тим самим виразом, що і функція g[x,n], але замість суми необхідно обчислити добуток і навпаки.
Задано sп=-5, sк=5, s=1, t=5. Відповідно до номера варіанту потрібно розробити програму для одновимірного табулювання функцій g1[x,n], g2[x,n]/q1[x,n], q2[x,n], pe[s,t] і pf[s,t] за незалежною змінною Х згідно з математичними виразами, наведеними вище. Побудувати одновимірні графіки цих функцій.
Задача 7.4. Задано дійсне число s=1.32№ (де № – номер варіанту) і додатне ціле t=3. Відповідно до номера варіанту потрібно розробити програму, яка б давала змогу отримати значення функції
 ,
,
де h[x,y] визначається з таких математичних виразів:
1)
|
6)
|
11)
|
2)
|
7)
|
12)
|
3)
|
8)
|
13)
|
4)
|
9)
|
14)
|
5)
|
10)
|
15)
|
Задано sп=-5, sк=5, s=1, t=3. Відповідно до номера варіанту потрібно розробити програму для одновимірного табулювання функцій h1[x,y], max{h2; h3}, min{h4; h5}, we[s,t] і wf[s,t] за незалежною змінною Х згідно з математичними виразами, наведеними вище. Побудувати одновимірні графіки цих функцій.
7.5. Контрольні запитання
1. Навести приклади використання функції сторінки ИСТИНА
2. Навести приклади використання функції сторінки ЛОЖЬ
3. Навести приклади використання функції сторінки ЕСЛИ
4. Навести приклади використання функції сторінки И
Розрахункова робота №1. РОЗРОБЛЕННЯ ПРОГРАМНОГО ЗАБЕЗПЕЧЕННЯ ДЛЯ РОЗВ'ЯЗАННЯ МАТЕМАТИЧНОЇ ЗАДАЧІ
1.1. Програма роботи
2. Індивідуальні завдання
РОЗРАХУНКОВА РОБОТА №1 Завдання № 1
Задано дійсне число s=3,75 та цілі числа m=5 і n=5. Потрібно скласти програму, яка б давала змогу отримати значення елементів функції та побудувати її графік
![]() ,
,
де функції f[x,y,z] та q[x,y,z] визначаються з таких математичних виразів:
![]() ,
,
 ,
,
де
t – середня кількість додатних
елементів матриці
![]() ,
які знаходяться у кожному з її стовпців
,
які знаходяться у кожному з її стовпців
![]() .
.
Значення елементів матриць:
![]() і
і
![]()
визначаються за такими математичними виразами:
![]()
![]() .
.
Елементи
вектора-стовпця
![]() і матриці
визначаються за такими формулами:
і матриці
визначаються за такими формулами:
 ;
;
 .
.
На власний розсуд потрібно скласти програму для одно- чи двовимірного табулювання функції f[x,y,z] чи q[x,y,z] і побудувати її графік з нанесенням відповідних легенд. Межі та крок табулювання необхідно прийняти самостійно.
РОЗРАХУНКОВА РОБОТА №1 Завдання № 2
Задано дійсне число s=3,75 та цілі числа m=5 і n=5. Потрібно скласти програму, яка б давала змогу отримати значення елементів функції та побудувати її графік
![]() ,
,
де функції f[x,y,z] та q[x,y,z] визначаються з таких математичних виразів:
![]() ,
,
![]() ,
,
де t – середня кількість додатних елементів матриці , які знаходяться у кожному із її стовпців, що мають парні номери
![]() .
.
Значення елементів матриць:
і
визначаються за такими математичними виразами:
![]()
![]() .
.
Елементи вектора-стовпця і матриці визначаються за такими формулами:
 ;
;
 .
.
На власний розсуд потрібно скласти програму для одно- чи двовимірного табулювання функції f[x,y,z] чи q[x,y,z] і побудувати її графік з нанесенням відповідних легенд. Межі та крок табулювання необхідно прийняти самостійно.
РОЗРАХУНКОВА РОБОТА №1 Завдання № 3
Задано дійсне число s=3,75 та цілі числа m=5 і n=5. Потрібно скласти програму, яка б давала змогу отримати значення елементів функції та побудувати її графік
 ,
,
де функції f[x,y,z] та q[x,y,z] визначаються з таких математичних виразів:
![]() ,
,
![]() ,
,
де t – середня кількість від'ємних елементів матриці , які знаходяться у кожному із її стовпців, що мають непарні номери
![]() .
.
Значення елементів матриць:
і
визначаються за такими математичними виразами:
![]()
![]() .
.
Елементи вектора-стовпця і матриці визначаються за такими формулами:
![]() ;
;
 .
.
На власний розсуд потрібно скласти програму для одно- чи двовимірного табулювання функції f[x,y,z] чи q[x,y,z] і побудувати її графік з нанесенням відповідних легенд. Межі та крок табулювання необхідно прийняти самостійно.
РОЗРАХУНКОВА РОБОТА №1 Завдання № 4
Задано дійсне число s=3,75 та цілі числа m=5 і n=5. Потрібно скласти програму, яка б давала змогу отримати значення елементів функції та побудувати її графік
 ,
,
де функції f[x,y,z] та q[x,y,z] визначаються з таких математичних виразів:
![]() ,
,
![]() ,
,
де t – найменша сума додатних елементів матриці , які знаходяться у кожному із її рядків:
![]() .
.
Значення елементів матриць:
і
визначаються за такими математичними виразами:
![]()
![]() .
.
Елементи вектора-стовпця і матриці визначаються за такими формулами:
 ;
;
 .
.
На власний розсуд потрібно скласти програму для одно- чи двовимірного табулювання функції f[x,y,z] чи q[x,y,z] і побудувати її графік з нанесенням відповідних легенд. Межі та крок табулювання необхідно прийняти самостійно.
РОЗРАХУНКОВА РОБОТА №1 Завдання № 5
Задано дійсне число s=3,75 та цілі числа m=5 і n=5. Потрібно скласти програму, яка б давала змогу отримати значення елементів функції та побудувати її графік
![]()
де функції f[x,y,z] та q[x,y,z] визначаються з таких математичних виразів:
![]() ,
,
![]() ,
,
де t – найменша сума додатних елементів матриці , які знаходяться у кожному із її рядків, які мають парні номери
![]() .
.
Значення елементів матриць:
і
визначаються за такими математичними виразами:
![]() .
.
Елементи вектора-стовпця і матриці визначаються за такими формулами:
![]() ;
;
 .
.
На власний розсуд потрібно скласти програму для одно- чи двовимірного табулювання функції f[x,y,z] чи q[x,y,z] і побудувати її графік з нанесенням відповідних легенд. Межі та крок табулювання необхідно прийняти самостійно.
РОЗРАХУНКОВА РОБОТА №1 Завдання № 6
Задано дійсне число s=3,75 та цілі числа m=5 і n=5. Потрібно скласти програму, яка б давала змогу отримати значення елементів функції та побудувати її графік
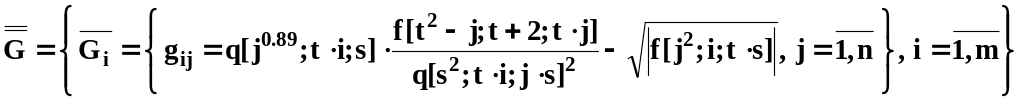 ,
,
де функції f[x,y,z] та q[x,y,z] визначаються з таких математичних виразів:
![]() ,
,
![]() ,
,
де t – найменша сума від'ємних елементів матриці , які знаходяться у кожному із її рядків, що мають непарні номери
![]() .
.
Значення елементів матриць:
і
визначаються за такими математичними виразами:
![]()
![]() .
.
Елементи вектора-стовпця і матриці визначаються за такими формулами:
 ;
;
.
На власний розсуд потрібно скласти програму для одно- чи двовимірного табулювання функції f[x,y,z] чи q[x,y,z] і побудувати її графік з нанесенням відповідних легенд. Межі та крок табулювання необхідно прийняти самостійно.
РОЗРАХУНКОВА РОБОТА №1 Завдання № 7
Задано дійсне число s=3,75 та цілі числа m=5 і n=5. Потрібно скласти програму, яка б давала змогу отримати значення елементів функції та побудувати її графік
 ,
,
де функції f[x,y,z] та q[x,y,z] визначаються з таких математичних виразів:
,
![]() ,
,
де t – найменше із середньоарифметичних значень від'ємних елементів кожного із стовпців матриці , поділених на її найбільший елемент:
![]() .
.
Значення елементів матриць:
і
визначаються за такими математичними виразами:
![]()
![]() .
.
Елементи вектора-стовпця і матриці визначаються за такими формулами:
![]() ;
;
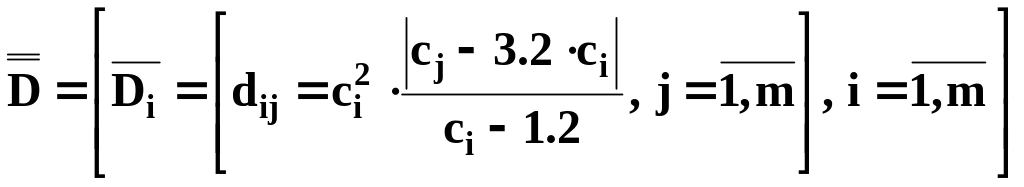 .
.
На власний розсуд потрібно скласти програму для одно- чи двовимірного табулювання функції f[x,y,z] чи q[x,y,z] і побудувати її графік з нанесенням відповідних легенд. Межі та крок табулювання необхідно прийняти самостійно.
РОЗРАХУНКОВА РОБОТА №1 Завдання № 8
Задано дійсне число s=3,75 та цілі числа m=5 і n=5. Потрібно скласти програму, яка б давала змогу отримати значення елементів функції та побудувати її графік
 ,
,
де функції f[x,y,z] та q[x,y,z] визначаються з таких математичних виразів:
![]() ,
,
![]() ,
,
де t – найменше із середньоарифметичних значень від'ємних елементів кожного із стовпців матриці , які мають парні номери
![]() .
.
Значення елементів матриць:
і
визначаються за такими математичними виразами:
![]()
![]() .
.
Елементи вектора-стовпця і матриці визначаються за такими формулами:
 ;
;
.
На власний розсуд потрібно скласти програму для одно- чи двовимірного табулювання функції f[x,y,z] чи q[x,y,z] і побудувати її графік з нанесенням відповідних легенд. Межі та крок табулювання необхідно прийняти самостійно.
РОЗРАХУНКОВА РОБОТА №1 Завдання № 9
Задано дійсне число s=3,75 та цілі числа m=5 і n=5. Потрібно скласти програму, яка б давала змогу отримати значення елементів функції та побудувати її графік
![]()
де функції f[x,y,z] та q[x,y,z] визначаються з таких математичних виразів:
![]() ,
,
![]() ,
,
де t – найменше із середньоарифметичних значень від'ємних елементів кожного із стовпців матриці , які мають непарні номери
![]() .
.
Значення елементів матриць:
і
визначаються за такими математичними виразами:
![]()
![]() .
.
Елементи вектора-стовпця і матриці визначаються за такими формулами:
 ;
;
 .
.
На власний розсуд потрібно скласти програму для одно- чи двовимірного табулювання функції f[x,y,z] чи q[x,y,z] і побудувати її графік з нанесенням відповідних легенд. Межі та крок табулювання необхідно прийняти самостійно.
РОЗРАХУНКОВА РОБОТА №1 Завдання № 10
Задано дійсне число s=3,75 та цілі числа m=5 і n=5. Потрібно скласти програму, яка б давала змогу отримати значення елементів функції та побудувати її графік
![]() ,
,
де функції f[x,y,z] та q[x,y,z] визначаються з таких математичних виразів:
![]() ,
,
 ,
,
де t – найменше із найбільших значень додатних елементів кожного із рядків матриці , помножена на її найменший елемент:
![]() .
.
Значення елементів матриць:
і
визначаються за такими математичними виразами:
![]()
![]() .
.
Елементи вектора-стовпця і матриці визначаються за такими формулами:
![]() ;
;
 .
.
На власний розсуд потрібно скласти програму для одно- чи двовимірного табулювання функції f[x,y,z] чи q[x,y,z] і побудувати її графік з нанесенням відповідних легенд. Межі та крок табулювання необхідно прийняти самостійно.
РОЗРАХУНКОВА РОБОТА №1 Завдання № 11
Задано дійсне число s=3,75 та цілі числа m=5 і n=5. Потрібно скласти програму, яка б давала змогу отримати значення елементів функції та побудувати її графік
 ,
,
де функції f[x,y,z] та q[x,y,z] визначаються з таких математичних виразів:
 ,
,
![]() ,
,
де t – найменше із найбільших значень додатних елементів кожного із рядків матриці , які мають парні номери
![]() .
.
Значення елементів матриць:
і
визначаються за такими математичними виразами:
![]()
![]() ;
;
Елементи вектора-стовпця і матриці визначаються за такими формулами:
 ;
;
 .
.
На власний розсуд потрібно скласти програму для одно- чи двовимірного табулювання функції f[x,y,z] чи q[x,y,z] і побудувати її графік з нанесенням відповідних легенд. Межі та крок табулювання необхідно прийняти самостійно.
РОЗРАХУНКОВА РОБОТА №1 Завдання № 12
Задано дійсне число s=3,75 та цілі числа m=5 і n=5. Потрібно скласти програму, яка б давала змогу отримати значення елементів функції та побудувати її графік
 ,
,
де функції f[x,y,z] та q[x,y,z] визначаються з таких математичних виразів:
![]() ,
,
![]() ,
,
де t – найменше із найбільших значень додатних елементів кожного із рядків матриці , які мають непарні номери
![]() .
.
Значення елементів матриць:
і
визначаються за такими математичними виразами:
![]()
![]() .
.
Елементи вектора-стовпця і матриці визначаються за такими формулами:
 ;
;
.
На власний розсуд потрібно скласти програму для одно- чи двовимірного табулювання функції f[x,y,z] чи q[x,y,z] і побудувати її графік з нанесенням відповідних легенд. Межі та крок табулювання необхідно прийняти самостійно.
РОЗРАХУНКОВА РОБОТА №1 Завдання № 13
Задано дійсне число s=3,75 та цілі числа m=5 і n=5. Потрібно скласти програму, яка б давала змогу отримати значення елементів функції та побудувати її графік
![]()
де функції f[x,y,z] та q[x,y,z] визначаються з таких математичних виразів:
![]() ,
,
![]() ,
,
де t – сума мінімальних значень елементів матриці , які знаходяться у кожному із її рядків:
![]() .
.
Значення елементів матриць:
і
визначаються за такими математичними виразами:
![]()
![]() .
.
Елементи вектора-стовпця і матриці визначаються за такими формулами:
 ;
;
 .
.
На власний розсуд потрібно скласти програму для одно- чи двовимірного табулювання функції f[x,y,z] чи q[x,y,z] і побудувати її графік з нанесенням відповідних легенд. Межі та крок табулювання необхідно прийняти самостійно.
РОЗРАХУНКОВА РОБОТА №1 Завдання № 14
Задано дійсне число s=3,75 та цілі числа m=5 і n=5. Потрібно скласти програму, яка б давала змогу отримати значення елементів функції та побудувати її графік
![]() ,
,
де функції f[x,y,z] та q[x,y,z] визначаються з таких математичних виразів:
,
![]() ,
,
де t – сума мінімальних значень елементів матриці , які знаходяться у кожному із її стовпців, що мають парні номери
![]() .
.
Значення елементів матриць:
і
визначаються за такими математичними виразами:
![]()
![]() .
.
Елементи вектора-стовпця і матриці визначаються за такими формулами:
![]() ;
;
.
На власний розсуд потрібно скласти програму для одно- чи двовимірного табулювання функції f[x,y,z] чи q[x,y,z] і побудувати її графік з нанесенням відповідних легенд. Межі та крок табулювання необхідно прийняти самостійно.
РОЗРАХУНКОВА РОБОТА №1 Завдання № 15
Задано дійсне число s=3,75 та цілі числа m=5 і n=5. Потрібно скласти програму, яка б давала змогу отримати значення елементів функції та побудувати її графік
 ,
,
де функції f[x,y,z] та q[x,y,z] визначаються з таких математичних виразів:
![]() ,
,
![]() ,
,
де t – сума максимальних значень елементів матриці , які знаходяться у кожному із її рядків, що мають непарні номери
![]() .
.
Значення елементів матриць:
і
визначаються за такими математичними виразами:
![]() .
.
Елементи вектора-стовпця і матриці визначаються за такими формулами:
 ;
;
 .
.
На власний розсуд потрібно скласти програму для одно- чи двовимірного табулювання функції f[x,y,z] чи q[x,y,z] і побудувати її графік з нанесенням відповідних легенд. Межі та крок табулювання необхідно прийняти самостійно.
РОЗРАХУНКОВА РОБОТА №1 Завдання № 16
Задано дійсне число s=3,75 та цілі числа m=5 і n=5. Потрібно скласти програму, яка б давала змогу отримати значення елементів функції та побудувати її графік
 ,
,
де функції f[x,y,z] та q[x,y,z] визначаються з таких математичних виразів:
![]() ;
; ![]() ,
,
де t – сума мінімальних значень елементів матриці , які знаходяться у кожному із її стовпців, що мають парні номери
![]() .
.
Значення елементів матриць:
і
визначаються за такими математичними виразами:
![]() .
.
Елементи вектора-стовпця і матриці визначаються за такими формулами:
 ;
;
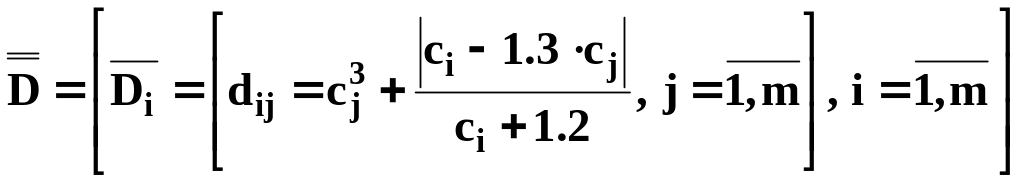 .
.
На власний розсуд потрібно скласти програму для одно- чи двовимірного табулювання функції f[x,y,z] чи q[x,y,z] і побудувати її графік з нанесенням відповідних легенд. Межі та крок табулювання необхідно прийняти самостійно.
РОЗРАХУНКОВА РОБОТА №1 Завдання № 17
Задано дійсне число s=3,75 та цілі числа m=5 і n=5. Потрібно скласти програму, яка б давала змогу отримати значення елементів функції та побудувати її графік
 ,
,
де функції f[x,y,z] та q[x,y,z] визначаються з таких математичних виразів:
![]() ;
,
;
,
де t – найменше із найбільших значень додатних елементів кожного із рядків матриці , які мають непарні номери
![]() .
.
Значення елементів матриць:
і
визначаються за такими математичними виразами:
![]()
![]() .
.
Елементи вектора-стовпця і матриці визначаються за такими формулами:
 ;
;
 .
.
На власний розсуд потрібно скласти програму для одно- чи двовимірного табулювання функції f[x,y,z] чи q[x,y,z] і побудувати її графік з нанесенням відповідних легенд. Межі та крок табулювання необхідно прийняти самостійно.
РОЗРАХУНКОВА РОБОТА №1 Завдання № 18
Задано дійсне число s=3,75 та цілі числа m=5 і n=5. Потрібно скласти програму, яка б давала змогу отримати значення елементів функції та побудувати її графік
 ,
,
де функції f[x,y,z] та q[x,y,z] визначаються з таких математичних виразів:
![]() ;
,
;
,
де t – найменше із найбільших значень додатних елементів кожного із рядків матриці , помножена на її найменший елемент:
![]() .
.
Значення елементів матриць:
і
визначаються за такими математичними виразами:
![]()
![]() .
.
Елементи вектора-стовпця і матриці визначаються за такими формулами:
![]() ;
;
 .
.
На власний розсуд потрібно скласти програму для одно- чи двовимірного табулювання функції f[x,y,z] чи q[x,y,z] і побудувати її графік з нанесенням відповідних легенд. Межі та крок табулювання необхідно прийняти самостійно.
РОЗРАХУНКОВА РОБОТА №1 Завдання № 19
Задано дійсне число s=3,75 та цілі числа m=5 і n=5. Потрібно скласти програму, яка б давала змогу отримати значення елементів функції та побудувати її графік
 ,
,
де функції f[x,y,z] та q[x,y,z] визначаються з таких математичних виразів:
![]() ;
; ![]() ,
,
де t – найменше із середньоарифметичних значень від'ємних елементів кожного із стовпців матриці , які мають непарні номери
![]() .
.
Значення елементів матриць:
і
визначаються за такими математичними виразами:
![]() .
.
Елементи вектора-стовпця і матриці визначаються за такими формулами:
 ;
;
 .
.
На власний розсуд потрібно скласти програму для одно- чи двовимірного табулювання функції f[x,y,z] чи q[x,y,z] і побудувати її графік з нанесенням відповідних легенд. Межі та крок табулювання необхідно прийняти самостійно.
РОЗРАХУНКОВА РОБОТА №1 Завдання № 20
Задано дійсне число s=3,75 та цілі числа m=5 і n=5. Потрібно скласти програму, яка б давала змогу отримати значення елементів функції та побудувати її графік
 ,
,
де функції f[x,y,z] та q[x,y,z] визначаються з таких математичних виразів:
![]() ;
,
;
,
де t – найменше із середньоарифметичних значень від'ємних елементів кожного із стовпців матриці , поділених на її найбільший елемент:
![]() .
.
Значення елементів матриць:
і
визначаються за такими математичними виразами:
![]() .
.
Елементи вектора-стовпця і матриці визначаються за такими формулами:
 ;
;
 .
.
На власний розсуд потрібно скласти програму для одно- чи двовимірного табулювання функції f[x,y,z] чи q[x,y,z] і побудувати її графік з нанесенням відповідних легенд. Межі та крок табулювання необхідно прийняти самостійно.
РОЗРАХУНКОВА РОБОТА №1 Завдання № 21
Задано дійсне число s=3,75 та цілі числа m=5 і n=5. Потрібно скласти програму, яка б давала змогу отримати значення елементів функції та побудувати її графік
 ,
,
де функції f[x,y,z] та q[x,y,z] визначаються з таких математичних виразів:
![]() ;
,
;
,
де t – сума максимальних значень елементів матриці , які знаходяться у кожному із її рядків, що мають непарні номери
![]() .
.
Значення елементів матриць:
і
визначаються за такими математичними виразами:
![]() .
.
Елементи вектора-стовпця і матриці визначаються за такими формулами:
 ;
;
![]() .
.
На власний розсуд потрібно скласти програму для одно- чи двовимірного табулювання функції f[x,y,z] чи q[x,y,z] і побудувати її графік з нанесенням відповідних легенд. Межі та крок табулювання необхідно прийняти самостійно.
РОЗРАХУНКОВА РОБОТА №1 Завдання № 22
Задано дійсне число s=3,75 та цілі числа m=5 і n=5. Потрібно скласти програму, яка б давала змогу отримати значення елементів функції та побудувати її графік
 ,
,
де функції f[x,y,z] та q[x,y,z] визначаються з таких математичних виразів:
![]() ;
,
;
,
де t – середня кількість додатних елементів матриці , які знаходяться у кожному з її стовпців:
![]() .
.
Значення елементів матриць:
і
визначаються за такими математичними виразами:
![]()
![]() .
.
Елементи вектора-стовпця і матриці визначаються за такими формулами:
 ;
;
 .
.
На власний розсуд потрібно скласти програму для одно- чи двовимірного табулювання функції f[x,y,z] чи q[x,y,z] і побудувати її графік з нанесенням відповідних легенд. Межі та крок табулювання необхідно прийняти самостійно.
РОЗРАХУНКОВА РОБОТА №1 Завдання № 23
Задано дійсне число s=3,75 та цілі числа m=5 і n=5. Потрібно скласти програму, яка б давала змогу отримати значення елементів функції та побудувати її графік
 ,
,
де функції f[x,y,z] та q[x,y,z] визначаються з таких математичних виразів:
![]() ;
,
;
,
де t – середня кількість додатних елементів матриці , які знаходяться у кожному із її стовпців, що мають парні номери
![]() .
.
Значення елементів матриць:
і
визначаються за такими математичними виразами:
![]()
![]() .
.
Елементи вектора-стовпця і матриці визначаються за такими формулами:
 ;
;
 .
.
На власний розсуд потрібно скласти програму для одно- чи двовимірного табулювання функції f[x,y,z] чи q[x,y,z] і побудувати її графік з нанесенням відповідних легенд. Межі та крок табулювання необхідно прийняти самостійно.
РОЗРАХУНКОВА РОБОТА №1 Завдання № 24
Задано дійсне число s=3,75 та цілі числа m=5 і n=5. Потрібно скласти програму, яка б давала змогу отримати значення елементів функції та побудувати її графік
 ,
,
де функції f[x,y,z] та q[x,y,z] визначаються з таких математичних виразів:
![]() ;
,
;
,
де t – середня кількість від'ємних елементів матриці , які знаходяться у кожному із її стовпців, що мають непарні номери
![]() .
.
Значення елементів матриць:
і
визначаються за такими математичними виразами:
![]() .
.
Елементи вектора-стовпця і матриці визначаються за такими формулами:
 ;
;
.
На власний розсуд потрібно скласти програму для одно- чи двовимірного табулювання функції f[x,y,z] чи q[x,y,z] і побудувати її графік з нанесенням відповідних легенд. Межі та крок табулювання необхідно прийняти самостійно.
РОЗРАХУНКОВА РОБОТА №1 Завдання № 25
Задано дійсне число s=3,75 та цілі числа m=5 і n=5. Потрібно скласти програму, яка б давала змогу отримати значення елементів функції та побудувати її графік
 ,
,
де функції f[x,y,z] та q[x,y,z] визначаються з таких математичних виразів:
![]() ;
; ![]() ,
,
де t – найменша сума додатних елементів матриці , які знаходяться у кожному із її рядків:
![]() .
.
Значення елементів матриць:
і
визначаються за такими математичними виразами:
![]()
![]() .
.
Елементи вектора-стовпця і матриці визначаються за такими формулами:
 ;
;
 .
.
На власний розсуд потрібно скласти програму для одно- чи двовимірного табулювання функції f[x,y,z] чи q[x,y,z] і побудувати її графік з нанесенням відповідних легенд. Межі та крок табулювання необхідно прийняти самостійно.
РОЗРАХУНКОВА РОБОТА №1 Завдання № 26
Задано дійсне число s=3,75 та цілі числа m=5 і n=5. Потрібно скласти програму, яка б давала змогу отримати значення елементів функції та побудувати її графік
 ,
,
де функції f[x,y,z] та q[x,y,z] визначаються з таких математичних виразів:
![]() ;
; ![]() ,
,
де t – найменша сума додатних елементів матриці , які знаходяться у кожному із її рядків, які мають парні номери
![]() .
.
Значення елементів матриць:
і
визначаються за такими математичними виразами:
![]() .
.
Елементи вектора-стовпця і матриці визначаються за такими формулами:
 ;
;
.
На власний розсуд потрібно скласти програму для одно- чи двовимірного табулювання функції f[x,y,z] чи q[x,y,z] і побудувати її графік з нанесенням відповідних легенд. Межі та крок табулювання необхідно прийняти самостійно.
РОЗРАХУНКОВА РОБОТА №1 Завдання № 27
Задано дійсне число s=3,75 та цілі числа m=5 і n=5. Потрібно скласти програму, яка б давала змогу отримати значення елементів функції та побудувати її графік
 ,
,
де функції f[x,y,z] та q[x,y,z] визначаються з таких математичних виразів:
![]() ;
; ![]() ,
,
де t – середня кількість додатних елементів матриці , які знаходяться у кожному з її стовпців:
![]() .
.
Значення елементів матриць:
і
визначаються за такими математичними виразами:
![]()
![]() .
.
Елементи вектора-стовпця і матриці визначаються за такими формулами:
![]() ;
;
 .
.
На власний розсуд потрібно скласти програму для одно- чи двовимірного табулювання функції f[x,y,z] чи q[x,y,z] і побудувати її графік з нанесенням відповідних легенд. Межі та крок табулювання необхідно прийняти самостійно.
РОЗРАХУНКОВА РОБОТА №1 Завдання № 28
Задано дійсне число s=3,75 та цілі числа m=5 і n=5. Потрібно скласти програму, яка б давала змогу отримати значення елементів функції та побудувати її графік
 ,
,
де функції f[x,y,z] та q[x,y,z] визначаються з таких математичних виразів:
![]() ;
,
;
,
де t – середня кількість додатних елементів матриці , які знаходяться у кожному із її стовпців, що мають парні номери
.
Значення елементів матриць:
і
визначаються за такими математичними виразами:
![]()
![]() ;
;
Елементи вектора-стовпця і матриці визначаються за такими формулами:
![]() ;
;
.
На власний розсуд потрібно скласти програму для одно- чи двовимірного табулювання функції f[x,y,z] чи q[x,y,z] і побудувати її графік з нанесенням відповідних легенд. Межі та крок табулювання необхідно прийняти самостійно.
РОЗРАХУНКОВА РОБОТА №1 Завдання № 29
Задано дійсне число s=3,75 та цілі числа m=5 і n=5. Потрібно скласти програму, яка б давала змогу отримати значення елементів функції та побудувати її графік
 ,
,
де функції f[x,y,z] та q[x,y,z] визначаються з таких математичних виразів:
![]() ;
; ![]() ,
,
де t – найменша сума додатних елементів матриці , які знаходяться у кожному із її рядків:
.
Значення елементів матриць:
і
визначаються за такими математичними виразами:
![]()
![]() .
.
Елементи вектора-стовпця і матриці визначаються за такими формулами:
![]() ;
;
.
На власний розсуд потрібно скласти програму для одно- чи двовимірного табулювання функції f[x,y,z] чи q[x,y,z] і побудувати її графік з нанесенням відповідних легенд. Межі та крок табулювання необхідно прийняти самостійно.
РОЗРАХУНКОВА РОБОТА №1 Завдання № 30
Задано дійсне число s=3,75 та цілі числа m=5 і n=5. Потрібно скласти програму, яка б давала змогу отримати значення елементів функції та побудувати її графік
 ,
,
де функції f[x,y,z] та q[x,y,z] визначаються з таких математичних виразів:
![]() ;
,
;
,
де t – сума мінімальних значень елементів матриці , які знаходяться у кожному із її стовпців, що мають парні номери
![]() .
.
Значення елементів матриць:
і
визначаються за такими математичними виразами:
![]()
![]() .
.
Елементи вектора-стовпця і матриці визначаються за такими формулами:
![]() ;
;
.
На власний розсуд потрібно скласти програму для одно- чи двовимірного табулювання функції f[x,y,z] чи q[x,y,z] і побудувати її графік з нанесенням відповідних легенд. Межі та крок табулювання необхідно прийняти самостійно.
РОЗРАХУНКОВА РОБОТА №1 Завдання № 31
Задано дійсне число s=3,75 та цілі числа m=5 і n=5. Потрібно скласти програму, яка б давала змогу отримати значення елементів функції та побудувати її графік
 ,
,
де функції f[x,y,z] та q[x,y,z] визначаються з таких математичних виразів:
![]() ;
,
;
,
де t – сума максимальних значень елементів матриці , які знаходяться у кожному із її рядків, що мають непарні номери
![]() .
.
Значення елементів матриць:
і
визначаються за такими математичними виразами:
![]()
![]() .
.
Елементи вектора-стовпця і матриці визначаються за такими формулами:
![]() ;
;
.
На власний розсуд потрібно скласти програму для одно- чи двовимірного табулювання функції f[x,y,z] чи q[x,y,z] і побудувати її графік з нанесенням відповідних легенд. Межі та крок табулювання необхідно прийняти самостійно.
РОЗРАХУНКОВА РОБОТА №1 Завдання № 32
Задано дійсне число s=3,75 та цілі числа m=5 і n=5. Потрібно скласти програму, яка б давала змогу отримати значення елементів функції та побудувати її графік
 ,
,
де функції f[x,y,z] та q[x,y,z] визначаються з таких математичних виразів:
![]() ;
,
;
,
де t – найменше із середньоарифметичних значень від'ємних елементів кожного із стовпців матриці , поділених на її найбільший елемент:
![]() .
.
Значення елементів матриць:
і
визначаються за такими математичними виразами:
![]()
![]() .
.
Елементи вектора-стовпця і матриці визначаються за такими формулами:
![]() ;
;
.
На власний розсуд потрібно скласти програму для одно- чи двовимірного табулювання функції f[x,y,z] чи q[x,y,z] і побудувати її графік з нанесенням відповідних легенд. Межі та крок табулювання необхідно прийняти самостійно.

 ;
; ;
; ;
;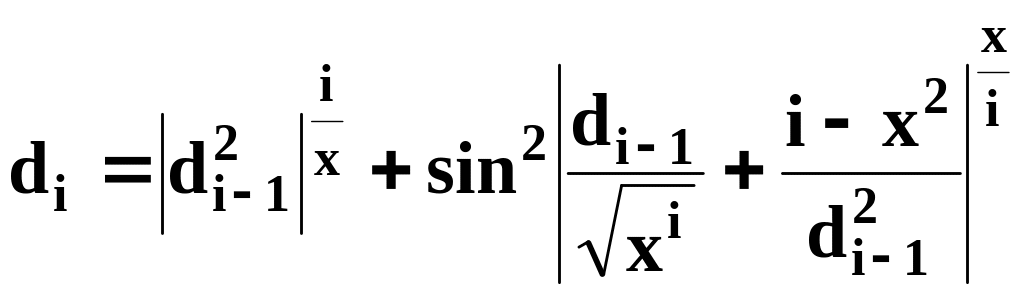 ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
;


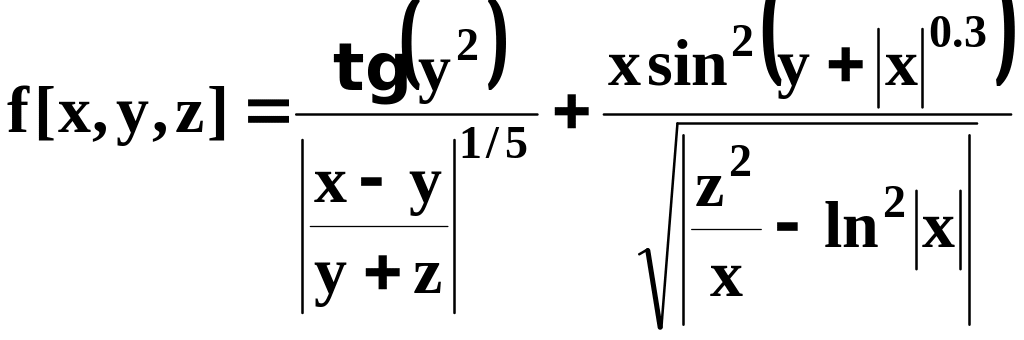

 .
.